Difficulty Level 2: – Medium
Directions: Solve each problem and then click on the correct answer. You are permitted to use a calculator on this test.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
If $A$ and $B$ are the solutions to the equation $x^2 − 23x + 130 = 0$, what is the sum of $A$ and $B$?
$−10$ | |
$10$ | |
$23$ | |
$33$ | |
$50$ |
Question 1 Explanation:
The correct answer is (C). In order to factor the expression provided, we need to find two factors of 130 whose sum is −23. Two such factors are −10 and −13:
$−10 * −13 = 130 \,$ and $\, −10 + −13 = −23$
So $(x − 13)(x − 10) = 0$
$x = 10, 13$
Their sum is 23.
$−10 * −13 = 130 \,$ and $\, −10 + −13 = −23$
So $(x − 13)(x − 10) = 0$
$x = 10, 13$
Their sum is 23.
Question 2 |
Which of these is true for all real numbers $x$ and $y$ such that $x > 0$ and $y < 0$?
$xy \gt 0$ | |
$x + y \gt 0$ | |
$x + y \lt 0$ | |
$x^2 + y^2 \gt 0$ | |
$x − y \lt 0$ |
Question 2 Explanation:
The correct answer is (D). For this question, you have to examine all the answer options individually in order to eliminate all those that cannot be true. First, if $x$ is positive and $y$ is negative, their product must be negative, so (A) is incorrect.
Next, the sum of a positive and a negative number could be either positive or negative, depending on which number has the greater absolute value; this rules out (B) and (C) because neither one of those is always true.
Similar reasoning applies to choice (E) as well. However, both positive and negative real numbers have positive squares, and adding those positive squares will always yield a positive number, so (D) is correct.
Next, the sum of a positive and a negative number could be either positive or negative, depending on which number has the greater absolute value; this rules out (B) and (C) because neither one of those is always true.
Similar reasoning applies to choice (E) as well. However, both positive and negative real numbers have positive squares, and adding those positive squares will always yield a positive number, so (D) is correct.
Question 3 |
At what point on the Cartesian plane do the following two lines intersect?
$y = 3x - 17$ $\text{and}$ $y = -2x + 13$
$(8, 7)$ | |
$(6, 1)$ | |
$(-3, 4)$ | |
$(7, -1)$ | |
$(5, 2)$ |
Question 3 Explanation:
The correct answer is (B). Since both equations already have the variable $y$ isolated, we can set them equal to each other and solve for $x$:
$3x - 17 = -2x + 13$
$5x = 30$
$x = 6$
Only answer choice (B) has an $x$ coordinate of $6$. Therefore, there is no need to solve for $y$.
$3x - 17 = -2x + 13$
$5x = 30$
$x = 6$
Only answer choice (B) has an $x$ coordinate of $6$. Therefore, there is no need to solve for $y$.
Question 4 |
The number of people who have seen a certain video is modeled by the equation $y = 10(1.5)^x$, where $x$ is the number of hours that have passed since the video’s release and $y$ is the number of people who have seen the video.
Approximately how many people are predicted to have seen the video $8$ hours after its release?
$911$ | |
$701$ | |
$256$ | |
$591$ | |
$412$ |
Question 4 Explanation:
The correct answer is (C). We are asked to find the number of people who have seen the video after 8 hours. In other words, we want the value of $y$ when $x = 8$.
$y = 10(1.5)^x$
$y = 10(1.5)^8$
$y ≈ 10(25.63)$
$y ≈ 256$
$y = 10(1.5)^x$
$y = 10(1.5)^8$
$y ≈ 10(25.63)$
$y ≈ 256$
Question 5 |
What is the slope of the line represented by the equation $y = 2(3x + 4)$?
$2$ | |
$3$ | |
$5$ | |
$6$ | |
$4$ |
Question 5 Explanation:
The correct answer is (D). To determine the slope, it will be easiest if we first get the equation into slope-intercept form:
$y = mx + b$
$y = 2(3x + 4)$
Distribute the 2:
$y = (2)(3x) + (2)(4)$
$y = 6x + 8$
Now that the equation is in slope-intercept form, we see that the slope, $m$, is 6.
$y = mx + b$
$y = 2(3x + 4)$
Distribute the 2:
$y = (2)(3x) + (2)(4)$
$y = 6x + 8$
Now that the equation is in slope-intercept form, we see that the slope, $m$, is 6.
Question 6 |
If the side length of a square is $z$ units, what is the length of its diagonal in terms of $z$?
$z + 1$ | |
$z$ | |
$z\sqrt{2}$ | |
$z^2$ | |
$2z$ |
Question 6 Explanation:
The correct answer is (C). Recall that the diagonal of a square cuts it into 2 right triangles with side length ratios of $x$, $x$, $x \sqrt{2}$. With side length of $z$, the diagonal will be $z\sqrt{2}$.
Question 7 |
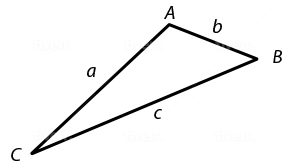
The triangle $ABC$ that is provided has side lengths of $a$, $b$, and $c$ feet and is not a right triangle. Let $A’$ be the image when the triangle is reflected across side $BC$.
Which of the following is an expression for the perimeter, in feet, of quadrilateral $A’BAC?$
$2ab$ | |
$2(a + b) − c$ | |
$a + b + 2c$ | |
$2(b + c)$ | |
$2(a + b)$ |
Question 7 Explanation:
The correct answer is (E). One approach this question is to draw it.
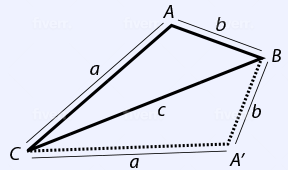 For the resulting quadrilateral $A'BAC$, length $c$ will not be included in the perimeter (since $CB$ is a diagonal of the quadrilateral, not a side).
For the resulting quadrilateral $A'BAC$, length $c$ will not be included in the perimeter (since $CB$ is a diagonal of the quadrilateral, not a side).
All the answer choices with length $c$ can be eliminated—which leaves us with just (A) and (E).
The perimeter can be found by adding up the lengths of the sides:
$a + a + b + b$
$= 2a + 2b$
$= 2(a + b)$
 For the resulting quadrilateral $A'BAC$, length $c$ will not be included in the perimeter (since $CB$ is a diagonal of the quadrilateral, not a side).
For the resulting quadrilateral $A'BAC$, length $c$ will not be included in the perimeter (since $CB$ is a diagonal of the quadrilateral, not a side).
All the answer choices with length $c$ can be eliminated—which leaves us with just (A) and (E).
The perimeter can be found by adding up the lengths of the sides:
$a + a + b + b$
$= 2a + 2b$
$= 2(a + b)$
Question 8 |
If 60% of a number is 12, what is 165% of the same number?
$20$ | |
$22$ | |
$28$ | |
$30$ | |
$33$ |
Question 8 Explanation:
The correct answer is (E). Translate the given expressions into equations:
$60\% \text{ of } x = 12$
$0.60 \ast x = 12$
$x = 20$
$165\% \text{ of } x$
$1.65 \ast 20 = 33$
$60\% \text{ of } x = 12$
$0.60 \ast x = 12$
$x = 20$
$165\% \text{ of } x$
$1.65 \ast 20 = 33$
Question 9 |
The ratio of circle $A$’s circumference to circle $B$’s circumference is 2:9, what is the ratio of their areas?
$1:18$ | |
$4:18$ | |
$4:81$ | |
$1:9$ | |
$2:81$ |
Question 9 Explanation:
The correct answer is (C). Circumference is a measurement of length (one-dimensional). Area is a two-dimensional measurement.
If the circumferences of A and B are in the ratio 2:9, the areas of A and B will be in the ratio:
$2^2:9^2$
$4:81$
A more detailed explanation follows:
Let the circumference of the smaller circle be: $c = 2 \pi r$
Let the circumference of the larger circle be: $C = 2 \pi R$
We are told that the ratio of circle A’s circumference to circle B’s circumference is 2:9. Thus:
$\dfrac{c}{C}=\dfrac{2πr}{2πR}=\dfrac{r}{R}=\dfrac{2}{9}$
The area of circle A with radius ‘$r$’ is $πr^2$
The area of circle B with radius ‘$R$’ is $πR^2$
The ratio of the areas of the two circles is:
$\dfrac{πr^2}{πR^2}=\dfrac{r^2}{R^2}=\left(\dfrac{r}{R}\right)^2$
So, the ratio of the areas of the two circles is equal to the square of the ratio of the radii of the two circles. We can substitute the ratio of the radii obtained above into the formula for the ratio of the areas:
The ratio of the areas of the two circles is:
$\left(\dfrac{r}{R}\right)^2=\left(\dfrac{2}{9}\right)^2=\dfrac{4}{81}$
If the circumferences of A and B are in the ratio 2:9, the areas of A and B will be in the ratio:
$2^2:9^2$
$4:81$
A more detailed explanation follows:
Let the circumference of the smaller circle be: $c = 2 \pi r$
Let the circumference of the larger circle be: $C = 2 \pi R$
We are told that the ratio of circle A’s circumference to circle B’s circumference is 2:9. Thus:
$\dfrac{c}{C}=\dfrac{2πr}{2πR}=\dfrac{r}{R}=\dfrac{2}{9}$
The area of circle A with radius ‘$r$’ is $πr^2$
The area of circle B with radius ‘$R$’ is $πR^2$
The ratio of the areas of the two circles is:
$\dfrac{πr^2}{πR^2}=\dfrac{r^2}{R^2}=\left(\dfrac{r}{R}\right)^2$
So, the ratio of the areas of the two circles is equal to the square of the ratio of the radii of the two circles. We can substitute the ratio of the radii obtained above into the formula for the ratio of the areas:
The ratio of the areas of the two circles is:
$\left(\dfrac{r}{R}\right)^2=\left(\dfrac{2}{9}\right)^2=\dfrac{4}{81}$
Question 10 |
Which coordinates satisfy the inequality: $y + 3 \gt −3(x − 2)$
$(−1, −2)$ | |
$(0, 2)$ | |
$(1, 0)$ | |
$(3, -3)$ | |
$(2, − 4)$ |
Question 10 Explanation:
The correct answer is (D). Solve the inequality for one variable:
$y + 3 > −3(x - 2)$
Test each answer choice to see which one satisfies the inequality.
$\text{(A) Test}$ $(-1, -2)$; $x = -1$ and $y = -2$
$-2 + 3 > -3(-1-2)$
$1 > 9$
Does not satisfy the inequality
$\text{(B) Test}$ $(0, 2)$; $x = 0$ and $y = 2$
$2 + 3 > -3(0 - 2)$
$5 > 6$
Does not satisfy the inequality
$\text{(C) Test}$ $(1, 0)$; $x = 1$ and $y = 0$
$0 + 3 > -3(1 - 2)$
$3 > 3$
Does not satisfy the inequality
$\text{(D) Test}$ $(3, -3)$; $x = 3$ and $y = -3$
$-3 + 3 > -3(3 - 2)$
$0 > -3$
Satisfies the inequality. (We could stop at this point.)
$\text{(E) Test}$ $(2, -4)$; $x = 2$ and $y = -4$
$-4 + 3 > -3(2 - 2)$
$-1 > 0$
Does not satisfy the inequality
$y + 3 > −3(x - 2)$
Test each answer choice to see which one satisfies the inequality.
$\text{(A) Test}$ $(-1, -2)$; $x = -1$ and $y = -2$
$-2 + 3 > -3(-1-2)$
$1 > 9$
Does not satisfy the inequality
$\text{(B) Test}$ $(0, 2)$; $x = 0$ and $y = 2$
$2 + 3 > -3(0 - 2)$
$5 > 6$
Does not satisfy the inequality
$\text{(C) Test}$ $(1, 0)$; $x = 1$ and $y = 0$
$0 + 3 > -3(1 - 2)$
$3 > 3$
Does not satisfy the inequality
$\text{(D) Test}$ $(3, -3)$; $x = 3$ and $y = -3$
$-3 + 3 > -3(3 - 2)$
$0 > -3$
Satisfies the inequality. (We could stop at this point.)
$\text{(E) Test}$ $(2, -4)$; $x = 2$ and $y = -4$
$-4 + 3 > -3(2 - 2)$
$-1 > 0$
Does not satisfy the inequality
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 10 questions to complete.
|
List |
Next Practice Test:
ACT Math Practice Test 5 >>
More Practice Tests:
ACT Math – Main Menu >>
ACT Science Practice >>
ACT English Practice >>
ACT Reading Practice >>
