Difficulty Level – 4: Difficult
Directions: Solve each problem and then click on the correct answer. You are permitted to use a calculator on this test.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
In a competition where the highest score wins, the scores of the top four competitors are consecutive even integers whose sum is 36. What is the score of the competitor who finished in second place?
$6$ | |
$8$ | |
$10$ | |
$12$ | |
$14$ |
Question 1 Explanation:
The correct answer is (C). For our situation, we will let $x$ represent the least of the four even scores.
The four consecutive even scores will be represented as:
$x, x + 2, x + 4, x + 6$
Use an equation to represent the situation:
$x + (x + 2) + (x + 4) $ $ + \; (x + 6) $ $ = 36$
$4x + 12 = 36$
$4x = 24$
$x = 6$
The score of the competitor who finished in second place will be:
$x + 4 = 6 + 4 = 10$
The four consecutive even scores will be represented as:
$x, x + 2, x + 4, x + 6$
Use an equation to represent the situation:
$x + (x + 2) + (x + 4) $ $ + \; (x + 6) $ $ = 36$
$4x + 12 = 36$
$4x = 24$
$x = 6$
The score of the competitor who finished in second place will be:
$x + 4 = 6 + 4 = 10$
Question 2 |
A company will be using a pie chart to represent the total expenditures of each department. The breakdown of its expenditures is as follows:
-
19% Research and Development
-
33% Marketing
-
22% Payroll
If the remaining expenditures represent $12,250, what is the dollar amount spent on Research and Development (Round to nearest unit)?
$7750$ | |
$7927$ | |
$8331$ | |
$8952$ | |
$9113$ |
Question 2 Explanation:
The correct answer is (D). Because they will use a pie chart, we know the percentages spent on each department will add up to 100%, meaning the "remaining expenditures" represent 26% of all expenditures. We can set up a proportion between the 19% spent on R&D and the 26% spent on others:
$\dfrac{19}{26} = \dfrac {x}{12{,}250}$
$(19)(12250) = (26)(x)$
$x = \dfrac{(19)(12250)}{26}$
$x = 8951.9 ≈ 8952$
$\dfrac{19}{26} = \dfrac {x}{12{,}250}$
$(19)(12250) = (26)(x)$
$x = \dfrac{(19)(12250)}{26}$
$x = 8951.9 ≈ 8952$
Question 3 |
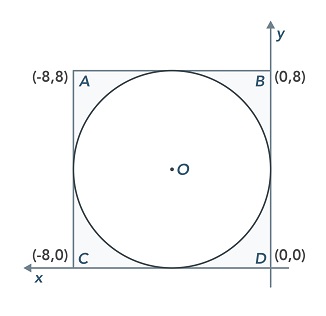
The vertices of square $ABCD$ have coordinates $(0,0)$, $(-8,0)$, $(-8,8)$, and $(0,8)$, and circle $O$ is inscribed in square $ABCD$.
Which of the following equations represents circle $O$?
$(x+4)^2+(y+4)^2=4$ | |
$(x −4)^2+(y −4)^2=16$ | |
$(x+4)^2+(y −4)^2=16$ | |
$(x+4)^2+(y-4)^2=4$ | |
$(x −4)^2+(y+4)^2=8$ |
Question 3 Explanation:
The correct answer is (C). The equation of a circle is given in the form $(x − a)^2 + (y − b)^2 = r^2$, where $a$ is the x-coordinate of the center point, $b$ is the y-coordinate of the center point, and $r$ is the radius.
Since square $ABCD$ has sides of length 8, we know that circle $O$ must have a radius of 4 units. Therefore, the equation of circle $O$ should end in the term 42 or 16. We can eliminate answers (A), (D), and (E), because they do not meet this condition.
The center of circle $O$ has an x-coordinate of −4, so we would expect circle $O$'s equation to contain the term $(x − (−4))^2$, or $(x + 4)^2$. This eliminates answer (B) from consideration, leaving us with answer (C) as the correct answer.
Since circle $O$ has center $(−4, 4)$ and radius 4, its full equation should read $(x + 4)^2 + (y − 4)^2 = 16$.
Since square $ABCD$ has sides of length 8, we know that circle $O$ must have a radius of 4 units. Therefore, the equation of circle $O$ should end in the term 42 or 16. We can eliminate answers (A), (D), and (E), because they do not meet this condition.
The center of circle $O$ has an x-coordinate of −4, so we would expect circle $O$'s equation to contain the term $(x − (−4))^2$, or $(x + 4)^2$. This eliminates answer (B) from consideration, leaving us with answer (C) as the correct answer.
Since circle $O$ has center $(−4, 4)$ and radius 4, its full equation should read $(x + 4)^2 + (y − 4)^2 = 16$.
Question 4 |
The average of 7 numbers is 24. The smallest of the numbers is 2 and the largest of the numbers is 31. What is the average of the middle 5 numbers?
$25$ | |
$27$ | |
$30$ | |
$31$ | |
$32$ |
Question 4 Explanation:
The correct answer is (B).
$\text{Avg of all }7 \text{ numbers} = $ $ \dfrac{\text{sum of all } 7 \text{ numbers}}{7}$
$24 = \dfrac{\text{sum of all } 7 \text{ numbers}}{7}$
$\text{Sum of all }7 \text{ numbers} $ $ = (7)(24) = 168$
$\text{Smallest } + (\text{Sum of middle } 5 ) $ $ + \text{ Largest} = 168$
$2 + (\text{Sum of middle } 5 ) + 31 = 168$
$\text{Sum of middle } 5 = 135$
$\text{Avg of middle } 5 = \dfrac{\text{Sum of middle } 5 }{5}$
$\text{Avg of middle } 5 = \dfrac{135}{5}$
$\text{Avg of middle } 5 = 27$
$\text{Avg of all }7 \text{ numbers} = $ $ \dfrac{\text{sum of all } 7 \text{ numbers}}{7}$
$24 = \dfrac{\text{sum of all } 7 \text{ numbers}}{7}$
$\text{Sum of all }7 \text{ numbers} $ $ = (7)(24) = 168$
$\text{Smallest } + (\text{Sum of middle } 5 ) $ $ + \text{ Largest} = 168$
$2 + (\text{Sum of middle } 5 ) + 31 = 168$
$\text{Sum of middle } 5 = 135$
$\text{Avg of middle } 5 = \dfrac{\text{Sum of middle } 5 }{5}$
$\text{Avg of middle } 5 = \dfrac{135}{5}$
$\text{Avg of middle } 5 = 27$
Question 5 |
Two side lengths of a triangle are 5 and 6, which of the following CANNOT be the length of the third side?
$2$ | |
$3$ | |
$5$ | |
$10$ | |
$12$ |
Question 5 Explanation:
The correct answer is (E). If a triangle has side lengths $a$, $b$, and $c$, the sum of the lengths of any 2 sides must be larger than the length of the 3rd side. So in this case 5 + 6 = 11 must be larger than side length $c$. From the answer choices, 12 is the only length greater than 11, so it cannot be the length of the third side.
Question 6 |
Danny wishes to shift the graph of the function $f(x) = x^2$ four places to the right and six places down from the origin $(0, 0)$. Which equation represents this translation?
$f(x) = (x − 6)^2 − 6$ | |
$f(x) = x − 4^2 + 6$ | |
$f(x) = x + 4^2 − 6$ | |
$f(x) = (x^2 − 4)^2 − 6$ | |
$fƒ(x) = (x − 4)^2 − 6$ |
Question 6 Explanation:
The correct answer is (E). The vertex form of a parabola is:
$a(x − h)^2 + k$, where $(h, k)$ represents the vertex.
We wish to translate our vertex from $(0, 0)$ to $(4, −6)$ so $h = 4$ and $k = −6$.
$f(x) = (x − 4)^2 − 6$
$a(x − h)^2 + k$, where $(h, k)$ represents the vertex.
We wish to translate our vertex from $(0, 0)$ to $(4, −6)$ so $h = 4$ and $k = −6$.
$f(x) = (x − 4)^2 − 6$
Question 7 |
The following input and output values represent a linear relationship. What number does the variable j represent?
$2$ | |
$3$ | |
$4$ | |
$5$ | |
$6$ |
Question 7 Explanation:
The correct answer is (B). If the numbers represent a functional relationship, then the slope of the line formed by each 2 points will be the same:
$\dfrac{j−5}{4−0}=\dfrac{2-j}{6-4}$
$\dfrac{j-5}{4}=\dfrac{2-j}{2}$
Cross multiply and solve for $j$:
$2j − 10 = 8 − 4j$
$6j = 18$
$j = 3$
An alternative approach is to observe that as the input increases by 4 (from −4 to 0), the output decreases by 2 (from 7 to 5). This means that when the input again increases by 4 (from 0 to 4), the output will again decrease by 2 (from 5 to $j$). Thus, $j$ must be 3.
$\dfrac{j−5}{4−0}=\dfrac{2-j}{6-4}$
$\dfrac{j-5}{4}=\dfrac{2-j}{2}$
Cross multiply and solve for $j$:
$2j − 10 = 8 − 4j$
$6j = 18$
$j = 3$
An alternative approach is to observe that as the input increases by 4 (from −4 to 0), the output decreases by 2 (from 7 to 5). This means that when the input again increases by 4 (from 0 to 4), the output will again decrease by 2 (from 5 to $j$). Thus, $j$ must be 3.
Question 8 |
Matrix A and Matrix B are multiplied together resulting in Matrix C. Use the information provided below to determine the values of $m$ and $n$
Formula for multiplying two $2 × 2$ matrices:

Given Matrices:
$\color{blue}A = \begin{bmatrix} 2 & 3 \\ 3 & 2 \\ \end{bmatrix}$$\color{red}B = \begin{bmatrix} 4 & m \\ 3 & n \\ \end{bmatrix}$
$\color{green}C = \color{blue}A × \color{red}B = \begin{bmatrix} 17 & 31 \\ 18 & 29 \\ \end{bmatrix}$
$m = 7$ and $n = 1$ | |
$m = 4$ and $n = 2$ | |
$m = 2$ and $n = 9$ | |
$m = 8$ and $n = 4$ | |
$m = 5$ and $n = 7$ |
Question 8 Explanation:
The correct answer is (E).
$A × B = C$
$ \begin{bmatrix} 2 & 3 \\ 3 & 2 \\ \end{bmatrix} × \begin{bmatrix} 4 & m \\ 3 & n \\ \end{bmatrix} $ $ = \begin{bmatrix} 17 & 31 \\ 18 & 29 \\ \end{bmatrix}$
$m$ and $n$ are located in positions $B_{12}$ and $B_{22}$, respectively. Based on the formula for matrix multiplication, we know:
$C_{12} = A_{11} × B_{12} + A_{12} × B_{22} $ $ = 2 × m + 3 × n$
$C_{22} = A_{21} × B_{12} + A_{22} × B_{22} $ $ = 3 × m + 2 × n$
We also know:
$C_{12} = 31$
$C_{22} = 29$
Substituting:
$31 = 2m + 3n$
$29 = 3m + 2n$
Solving the system of equations:
$m = 5$ and $n = 7$
Keep in mind that you can also work backwards from the given answer choices by substituting for $m$ and $n$ and seeing which choice creates a true equation.
$A × B = C$
$ \begin{bmatrix} 2 & 3 \\ 3 & 2 \\ \end{bmatrix} × \begin{bmatrix} 4 & m \\ 3 & n \\ \end{bmatrix} $ $ = \begin{bmatrix} 17 & 31 \\ 18 & 29 \\ \end{bmatrix}$
$m$ and $n$ are located in positions $B_{12}$ and $B_{22}$, respectively. Based on the formula for matrix multiplication, we know:
$C_{12} = A_{11} × B_{12} + A_{12} × B_{22} $ $ = 2 × m + 3 × n$
$C_{22} = A_{21} × B_{12} + A_{22} × B_{22} $ $ = 3 × m + 2 × n$
We also know:
$C_{12} = 31$
$C_{22} = 29$
Substituting:
$31 = 2m + 3n$
$29 = 3m + 2n$
Solving the system of equations:
$m = 5$ and $n = 7$
Keep in mind that you can also work backwards from the given answer choices by substituting for $m$ and $n$ and seeing which choice creates a true equation.
Question 9 |
Given that $\log_x a = 2$ and $\log_x b = 3$, what is the value of $\log_x(ab)^3$?
$6$ | |
$15$ | |
$36$ | |
$54$ | |
$216$ |
Question 9 Explanation:
The correct answer is (B). Using logarithmic identities, we can rewrite $\log_x (ab)^3$ as follows:
$\log_x(ab)^3 = 3\log_x(ab)$ ("Power Rule")
$3\log_x(ab) = 3(\log_xa + \log_xb)$ ("Product Rule")
We are given:
$\log_xa = 2$ and $\log_xb = 3$
Substituting we have:
$3(\log_xa + \log_xb) = 3(2 + 3) $ $ = 3(5) = 15$
$\log_x(ab)^3 = 3\log_x(ab)$ ("Power Rule")
$3\log_x(ab) = 3(\log_xa + \log_xb)$ ("Product Rule")
We are given:
$\log_xa = 2$ and $\log_xb = 3$
Substituting we have:
$3(\log_xa + \log_xb) = 3(2 + 3) $ $ = 3(5) = 15$
Question 10 |

There is to be a walkway built around a circular pond. The walkway will include a curved section extending most of the way around the pond and two straight sections, each measuring 15 feet, extending from the edges that meet in the center at a 90 degree angle to each other, as shown in the figure above. Which of the following is closest to the total length of the walkway, in feet?
$30$ | |
$65$ | |
$71$ | |
$101$ | |
$131$ |
Question 10 Explanation:
The correct answer is (D). The curved section extends all the way around the edge of the pond except for the part that is subtended by the 90-degree angle; therefore, its length is ¾ of the circumference of the circle, or $\frac{3}{4}(2πr)$.
The radius, $r$, is 15.
Length of the curved portion $= \frac{3}{4}(2π × 15) ≈ 70.7$
Each of the straight segments has length equal to the radius of the pond, or 15 feet, so the total length is around 70.7 + 15 + 15 = 100.7. The closest answer choice is (D) 101.
The radius, $r$, is 15.
Length of the curved portion $= \frac{3}{4}(2π × 15) ≈ 70.7$
Each of the straight segments has length equal to the radius of the pond, or 15 feet, so the total length is around 70.7 + 15 + 15 = 100.7. The closest answer choice is (D) 101.
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 10 questions to complete.
|
List |
Next Practice Test:
ACT Math Practice Test 8 >>
More Practice Tests:
ACT Math – Main Menu >>
ACT Science Practice >>
ACT English Practice >>
ACT Reading Practice >>
