Start your math test prep now with our free ACT Math Practice Tests. Topics covered include pre-algebra, elementary algebra, intermediate algebra, coordinate geometry, plane geometry, and trigonometry.
Difficulty Level – 1: Easy
Directions: Solve each problem and then click on the correct answer. You are permitted to use a calculator on this test.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
If $4x + 3x + 2(x + 5) = 28$, then $x = \; ?$
$1$ | |
$−1$ | |
$0$ | |
$−2$ | |
$2$ |
Question 1 Explanation:
The correct answer is (E).
$4x + 3x + 2(x + 5) = 28$
Begin by distributing the 2:
$4x + 3x + 2x + 10 = 28$
Combine like terms:
$9x + 10 = 28$
Subtract 10 from both sides:
$9x = 18$
Divide both sides by 9:
$x = 2$
Note that you can also work backwards and substitute each answer choice for $x$ to see which results in a true statement.
$4x + 3x + 2(x + 5) = 28$
Begin by distributing the 2:
$4x + 3x + 2x + 10 = 28$
Combine like terms:
$9x + 10 = 28$
Subtract 10 from both sides:
$9x = 18$
Divide both sides by 9:
$x = 2$
Note that you can also work backwards and substitute each answer choice for $x$ to see which results in a true statement.
Question 2 |
If the ratio of milk jugs to juice boxes is 13:$x$ and there are 39 milk jugs and 18 juice boxes, what is the value of $x$?
$4$ | |
$6$ | |
$8$ | |
$10$ | |
$12$ |
Question 2 Explanation:
The correct answer is (B). Solve this problem by setting up a proportion. We are told the ratio of milk to juice is 13:$x$ and that there are 39 milk and 18 juice:
$\dfrac{13}{x} = \dfrac{39}{18}$
Cross multiply and solve for $x$:
$(13)(18) = (x)(39)$
$234 = 39x$
Divide both sides by 39:
$6 = x$
$\dfrac{13}{x} = \dfrac{39}{18}$
Cross multiply and solve for $x$:
$(13)(18) = (x)(39)$
$234 = 39x$
Divide both sides by 39:
$6 = x$
Question 3 |
Triangle RST, shown below, is reflected across the $y$-axis to form triangle R’S’T’. What will be the coordinates of T’ in the resulting triangle R’S’T’?
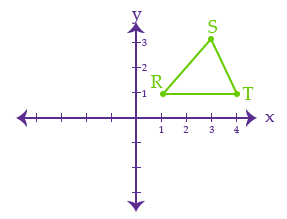
$(4, 1)$ | |
$(1, −4)$ | |
$(1, 4)$ | |
$(4, −1)$ | |
$(−4, 1)$ |
Question 3 Explanation:
The correct answer is (E). The coordinate of T in the original triangle is $(4,1)$.
After the triangle is reflected across the $y$-axis (vertical axis), T’ will be located at $(-4,1)$.
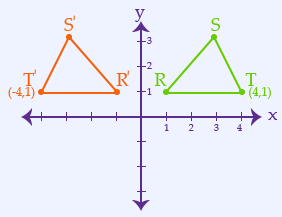
After the triangle is reflected across the $y$-axis (vertical axis), T’ will be located at $(-4,1)$.

Question 4 |
How many of the numbers between 20 and 40 are prime numbers?
$3$ | |
$4$ | |
$5$ | |
$6$ | |
$7$ |
Question 4 Explanation:
The correct answer is (B). A prime number is a number with no factors other than 1 and itself. Therefore, we can solve this problem by listing the numbers between 20 and 40 and eliminating those which are clearly divisible by some other number.
We only really need to list the odd numbers in this range, since the even numbers are obviously divisible by 2 and therefore not prime. 21, 23, 25, 27, 29, 31, 33, 35, 37, 39
Numbers divisible by 3: 21, 27, 33, 39
Numbers divisible by 5: 25, 35
The remaining numbers are 23, 29, 31, and 37. A quick check will tell us that none of these numbers are divisible by anything other than themselves and 1.
Therefore, 4 of the numbers between 20 and 40 are prime (Choice B).
We only really need to list the odd numbers in this range, since the even numbers are obviously divisible by 2 and therefore not prime. 21, 23, 25, 27, 29, 31, 33, 35, 37, 39
Numbers divisible by 3: 21, 27, 33, 39
Numbers divisible by 5: 25, 35
The remaining numbers are 23, 29, 31, and 37. A quick check will tell us that none of these numbers are divisible by anything other than themselves and 1.
Therefore, 4 of the numbers between 20 and 40 are prime (Choice B).
Question 5 |
If $\, a = −1$ and $\, b = 4$, what is the value of $\, a^3b +3b$?
$7$ | |
$16$ | |
$9$ | |
$8$ | |
$6$ |
Question 5 Explanation:
The correct answer is (D). Substitute the values for $a$ and $b$ into the expression:
$a^3b + 3b$
$(-1)^3(4) + 3(4)$
$(-1)(4) + 12$
$-4 + 12$
$= 8$
$a^3b + 3b$
$(-1)^3(4) + 3(4)$
$(-1)(4) + 12$
$-4 + 12$
$= 8$
Question 6 |
What is the least common multiple (the smallest integer that is divisible by all three numbers) of 3, 4, and 8?
$16$ | |
$12$ | |
$32$ | |
$96$ | |
$24$ |
Question 6 Explanation:
The correct answer is (E). The simplest approach is to make a list of the multiples of each of the three numbers, and then find the least multiple that appears in all three lists:
Multiples of 3:
3, 6, 9, 12, 15, 18, 21, 24, 27, 30
Multiples of 4:
4, 8, 12, 16, 20, 24, 28, 32, 36, 40
Multiples of 8:
8, 16, 24, 32, 40
The least common multiple is 24.
Multiples of 3:
3, 6, 9, 12, 15, 18, 21, 24, 27, 30
Multiples of 4:
4, 8, 12, 16, 20, 24, 28, 32, 36, 40
Multiples of 8:
8, 16, 24, 32, 40
The least common multiple is 24.
Question 7 |
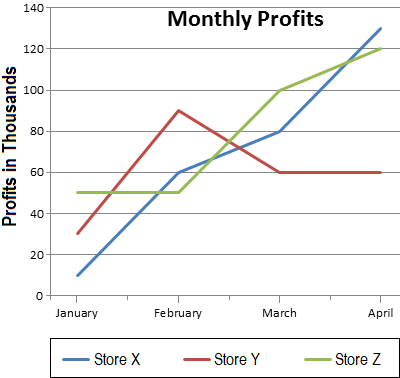
The chart above shows the monthly profits of 3 stores. What is the total profit generated by Store X and Store Z in the month of March?
$20{,}000$ | |
$80{,}000$ | |
$140{,}000$ | |
$180{,}000$ | |
$200{,}000$ |
Question 7 Explanation:
The correct answer is (D). From the chart we can see that Store X had 80 (thousand) in profits and Store Z had 100 (thousand) in profits. Combining these two, we arrive at 180 (thousand) in profits.
Question 8 |

The chart provided shows the monthly profits of 3 stores. By what amount did the profit of Store Y increase between January and February?
$\$30{,}000$ | |
$\$60{,}000$ | |
$\$90{,}000$ | |
$\$80{,}000$ | |
$\$40{,}000$ |
Question 8 Explanation:
The correct answer is (B). In January, Store Y made \$30,000. In February it made \$90,000.
The profit increased by \$60,000 (\$90,000 − \$30,000).
The profit increased by \$60,000 (\$90,000 − \$30,000).
Question 9 |
In order for the two triangles shown to be similar, what is the value of $x$ in inches?
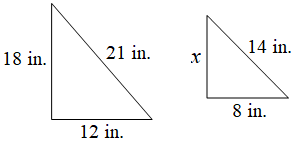
$12$ | |
$10$ | |
$14$ | |
$16$ | |
$15$ |
Question 9 Explanation:
The correct answer is (A). Problems involving similar triangles can be solved using equivalent proportions:
$\dfrac{x}{18} = \dfrac{8}{12}$
Cross multiply and solve:
$(x)(12) = (18)(8)$
$12x = 144$
$x = 12$
$\dfrac{x}{18} = \dfrac{8}{12}$
Cross multiply and solve:
$(x)(12) = (18)(8)$
$12x = 144$
$x = 12$
Question 10 |
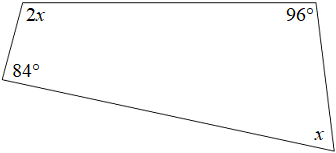
In quadrilateral WXYZ, what is the degree measurement of $x$? Recall that the sum of the interior angles of a quadrilateral is $360^°$.
$60^°$ | |
$75^°$ | |
$80^°$ | |
$90^°$ | |
$120^°$ |
Question 10 Explanation:
The correct answer is (A). The sum of the interior angles of a quadrilateral is 360°:
$84 + 96 + 2x + x = 360$
$180 + 3x = 360$
$3x = 180$
$x = 60$
$84 + 96 + 2x + x = 360$
$180 + 3x = 360$
$3x = 180$
$x = 60$
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 10 questions to complete.
|
List |
Next Practice Test:
ACT Math Practice Test 2 >>
More Practice Tests:
ACT Math – Main Menu >>
ACT Science Practice >>
ACT English Practice >>
ACT Reading Practice >>
