Difficulty Level – 1: Easy
Directions: Solve each problem and then click on the correct answer. You are permitted to use a calculator on this test.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
The graph provided corresponds with which linear equation?
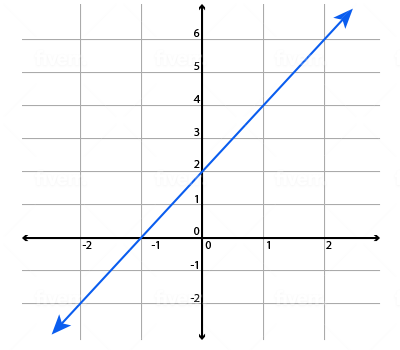
$y = 3x + 2$ | |
$y = 2x + 2$ | |
$y = 2x$ | |
$y = −2x − 2$ | |
$y = x + 2$ |
Question 1 Explanation:
The correct answer is (B). Recall the slope-intercept form of a line:
$y = mx + b$ where $m$ is the slope and $b$ is the y-intercept.
We can calculate the slope by finding the rise over the run from one point on the line to another. We can also use the formula:
$m=\dfrac{y_2-y_1}{x_2-x_1}$
It can be seen that the slope is equal to $\frac{2}{1}$. We can also see that the y-intercept is at y = 2. Only answer choice (B) has a slope of 2 and a y-intercept of 2.
$y = mx + b$ where $m$ is the slope and $b$ is the y-intercept.
We can calculate the slope by finding the rise over the run from one point on the line to another. We can also use the formula:
$m=\dfrac{y_2-y_1}{x_2-x_1}$
It can be seen that the slope is equal to $\frac{2}{1}$. We can also see that the y-intercept is at y = 2. Only answer choice (B) has a slope of 2 and a y-intercept of 2.
Question 2 |
What is the value of 251.293 + 112.98 + 12.023 rounded to the nearest hundredth?
$376.20$ | |
$376.29$ | |
$400.00$ | |
$376.00$ | |
$376.30$ |
Question 2 Explanation:
The correct answer is (E). It is not always helpful to use a calculator to answer ACT questions; however, this question and those similar in style are perfect for calculator use. Perform the required operation with your calculator to find 376.296 and because we are rounding to the nearest hundredth, and the thousandths place is a 6, we round up to 376.30.
Question 3 |
If $\, h(x) = 3x + 4$, what is $\, h(\frac{1}{2})?$
$\dfrac{3}{2}$ | |
$\dfrac{7}{2}$ | |
$\dfrac{9}{2}$ | |
$\dfrac{11}{2}$ | |
$\dfrac{5}{2}$ |
Question 3 Explanation:
The correct answer is (D).
To solve, we need to replace $x$ with $\frac{1}{2}$ in our function:
$h(x) = 3x + 4$
$h(\frac{1}{2}) = 3(\frac{1}{2}) + 4$
$h(\frac{1}{2}) = \frac{3}{2} + 4$
$h(\frac{1}{2}) = \frac{3}{2} + \frac{8}{2}$
$h(\frac{1}{2}) = \frac{11}{2}$
To solve, we need to replace $x$ with $\frac{1}{2}$ in our function:
$h(x) = 3x + 4$
$h(\frac{1}{2}) = 3(\frac{1}{2}) + 4$
$h(\frac{1}{2}) = \frac{3}{2} + 4$
$h(\frac{1}{2}) = \frac{3}{2} + \frac{8}{2}$
$h(\frac{1}{2}) = \frac{11}{2}$
Question 4 |
In the figure below, what is the length of altitude $y\,$?

$7$ $\text{cm}$ | |
$8$ $\text{cm}$ | |
$9$ $\text{cm}$ | |
$10$ $\text{cm}$ | |
$12$ $\text{cm}$ |
Question 4 Explanation:
The correct answer is (B).
Sometimes questions will provide unnecessary information, in this case the angle measurement of the top right angle. We can focus exclusively on the right triangle shown and use the Pythagorean Theorem (or the recognition of a Pythagorean triple) to find $y$:
Pythagorean Theorem: $a^2 + b^2 = c^2$
For our right triangle, we have:
$6^2 + y^2 = 10^2$
$36 + y^2 = 100$
$y^2 = 64$
$y = 8$
Sometimes questions will provide unnecessary information, in this case the angle measurement of the top right angle. We can focus exclusively on the right triangle shown and use the Pythagorean Theorem (or the recognition of a Pythagorean triple) to find $y$:
Pythagorean Theorem: $a^2 + b^2 = c^2$
For our right triangle, we have:
$6^2 + y^2 = 10^2$
$36 + y^2 = 100$
$y^2 = 64$
$y = 8$
Question 5 |
If $-\dfrac{5}{9}x = 10$, what is the value of $x$?
$−15$ | |
$10 \frac{5}{9}$ | |
$450$ | |
$16$ | |
$-18$ |
Question 5 Explanation:
The correct answer is (E).
$-\dfrac{5}{9}x = 10$
Multiply both sides by 9:
$9(-\frac{5}{9}x) = 9(10)$
$-5x = 90$
Divide both sides by −5:
$\dfrac{-5x}{-5} = \dfrac{90}{-5}$
$x = -18$
Note: You could also simply divide both sides by $-\frac{5}{9}$ if you have a calculator that handles fractions.
Keeping in mind that you can also work backwards from the answer choices until you find the one that works.
$-\dfrac{5}{9}x = 10$
Multiply both sides by 9:
$9(-\frac{5}{9}x) = 9(10)$
$-5x = 90$
Divide both sides by −5:
$\dfrac{-5x}{-5} = \dfrac{90}{-5}$
$x = -18$
Note: You could also simply divide both sides by $-\frac{5}{9}$ if you have a calculator that handles fractions.
Keeping in mind that you can also work backwards from the answer choices until you find the one that works.
Question 6 |
$\frac{1}{4}xy^2*16x^3y$
What is this expression equivalent to?
$8x^3y$ | |
$4x^4y^3$ | |
$4x^3y^4$ | |
$8x^3y^4$ | |
$16\frac{1}{4}x^4y^3$ |
Question 6 Explanation:
The correct answer is (B). To simplify this expression we will first multiply $\frac{1}{4}$ by 16. And then using the rules of exponent multiplication:
$x \ast x^3 = x^{1 + 3} = x^4$
$y^2 \ast y = y^{2 + 1} = y^3$
Combining these values:
$4x^4y^3$
$x \ast x^3 = x^{1 + 3} = x^4$
$y^2 \ast y = y^{2 + 1} = y^3$
Combining these values:
$4x^4y^3$
Question 7 |
Each term in a sequence of numbers is generated by multiplying the preceding term by 3, and then adding 2. If the first term is −3, what will the 6th term be?
$− 487$ | |
$− 165$ | |
$− 57$ | |
$57$ | |
$165$ |
Question 7 Explanation:
The correct answer is (A). Here is another question perfect for calculator use. Begin with –3 and follow the described procedure:
$−3 ∗ 3 + 2 = − 9 + 2 $ $ = −7 \,$ (2nd term)
$−7 ∗ 3 + 2 = −21 + 2 $ $ = −19 \,$ (3rd term)
$−19 ∗ 3 + 2 = −57 + 2 $ $ = −55 \,$ (4th term)
$−55 ∗ 3 + 2 = −165 + 2 $ $ = −163 \,$ (5th term)
$−163 ∗ 3 + 2 = −489 + 2 $ $ = −487 \,$ (6th term)
$−3 ∗ 3 + 2 = − 9 + 2 $ $ = −7 \,$ (2nd term)
$−7 ∗ 3 + 2 = −21 + 2 $ $ = −19 \,$ (3rd term)
$−19 ∗ 3 + 2 = −57 + 2 $ $ = −55 \,$ (4th term)
$−55 ∗ 3 + 2 = −165 + 2 $ $ = −163 \,$ (5th term)
$−163 ∗ 3 + 2 = −489 + 2 $ $ = −487 \,$ (6th term)
Question 8 |
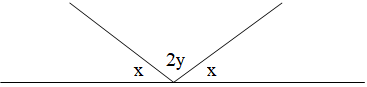
This figure shows a line broken into 3 adjacent angles.
If $2y = 120$, what is the value of $x$?
$30$ | |
$45$ | |
$60$ | |
$90$ | |
$120$ |
Question 8 Explanation:
The correct answer is (A). Begin by substituting the known value for 2$y$. Recall that a straight line is equal to 180°, so:
$x + x + 2y = 180$
$2x + 120 = 180$
$2x = 60$
$x = 30$
$x + x + 2y = 180$
$2x + 120 = 180$
$2x = 60$
$x = 30$
Question 9 |
A bag of marbles contains 3 green marbles, 7 red marbles, 2 white marbles, and 8 black marbles. If a marble is randomly chosen, what is the probability that the marble will NOT be green or white?
$25\%$ | |
$50\%$ | |
$60\%$ | |
$75\%$ | |
$80\%$ |
Question 9 Explanation:
The correct answer is (D). Recall that the probability of an event happening is:
$\frac{\text{Number of successful events}}{\text{Number of total events}}$
In this case, we are looking for the probability of selecting a marble that is neither green nor white:
$\frac{7 \text{ red} \, + \, 8 \text{ black}}{\text{Total Number of marbles}} $ $ =\frac{15}{20}= .75 = 75\%$
$\frac{\text{Number of successful events}}{\text{Number of total events}}$
In this case, we are looking for the probability of selecting a marble that is neither green nor white:
$\frac{7 \text{ red} \, + \, 8 \text{ black}}{\text{Total Number of marbles}} $ $ =\frac{15}{20}= .75 = 75\%$
Question 10 |
A family ordered 2 large pizzas for lunch. They ate $\frac{7}{8}$ of one pizza and $\frac{1}{4}$ of the other pizza. How much pizza was left for dinner?
$\dfrac{1}{8}$ | |
$\dfrac{3}{8}$ | |
$\dfrac{7}{8}$ | |
$1$ | |
$\dfrac{5}{4}$ |
Question 10 Explanation:
The correct answer is (C). When dealing with addition and subtraction involving fractions we must remember to always convert everything to a common denominator.
If the family consumed $\frac{7}{8}$ of one and $\frac{1}{4}$ or $\frac{2}{8}$ of the other pizza, they consumed a total of $\frac{9}{8}$ = $1\frac{1}{8}$.
We can now subtract the $\frac{1}{8}$ from the last remaining pizza to find $\frac{7}{8}$.
If the family consumed $\frac{7}{8}$ of one and $\frac{1}{4}$ or $\frac{2}{8}$ of the other pizza, they consumed a total of $\frac{9}{8}$ = $1\frac{1}{8}$.
We can now subtract the $\frac{1}{8}$ from the last remaining pizza to find $\frac{7}{8}$.
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 10 questions to complete.
|
List |
Next Practice Test:
ACT Math Practice Test 3 >>
More Practice Tests:
ACT Math – Main Menu >>
ACT Science Practice >>
ACT English Practice >>
ACT Reading Practice >>
