Difficulty Level – 3: Medium / Difficult
Directions: Solve each problem and then click on the correct answer. You are permitted to use a calculator on this test.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
A number, $x$, is decreased by 40% then increased by 25%. What is the final result in terms of $x$?
$0.55x$ | |
$0.575x$ | |
$0.65x$ | |
$0.7x$ | |
$0.75x$ |
Question 1 Explanation:
The correct answer is (E). To solve this, set $x$ = 100 and perform the operations. One hundred is a great number to choose here because 1% of 100 is 1.
$100 − 0.4 \ast 100 = 60$
$60 + 0.25 \ast 60 = 75$
Because $x$ = 100 was our initial value, we want to choose the answer choice that gives us 75 when we substitute 100 for $x$:
$ 0.75 \ast 100 = 75$
$100 − 0.4 \ast 100 = 60$
$60 + 0.25 \ast 60 = 75$
Because $x$ = 100 was our initial value, we want to choose the answer choice that gives us 75 when we substitute 100 for $x$:
$ 0.75 \ast 100 = 75$
Question 2 |
$\left(\dfrac{1}{3}y^\frac{1}{3}\right)^4*(2x^2y)^2=$
$\dfrac{4}{81}x^4y^\frac{10}{3}$ | |
$\dfrac{1}{81}x^2y^3$ | |
$\dfrac{4}{81}x^5y^\frac{9}{3}$ | |
$\dfrac{1}{81}x^2y^4$ | |
$\dfrac{4}{27}x^4y^\frac{8}{3}$ |
Question 2 Explanation:
The correct answer is (A). Evaluate the expression:
$\left(\dfrac{1}{3}y^{\frac{1}{3}}\right)^4 ⋅ \left(2x^2y\right)^2$
$\left(\dfrac{1}{3}\right)^4\left(y^{\frac{1}{3}}\right)^4 ⋅ (2)^2(x^2)^2(y)^2$
$\left(\dfrac{1}{81}\right)\left(y^{\frac{1}{3} ⋅ 4}\right)(4)(x^{2⋅2})(y^2)$
$\left(\dfrac{1}{81}\right)\left(y^{\frac{4}{3}}\right)(4)(x^4)(y^2)$
$\dfrac{4}{81}x^4y^{\frac{4}{3} + 2}$
$\dfrac{4}{81}x^4y^{\frac{4}{3} + \frac{6}{3}}$
$\dfrac{4}{81}x^4y^{\frac{10}{3}}$
$\left(\dfrac{1}{3}y^{\frac{1}{3}}\right)^4 ⋅ \left(2x^2y\right)^2$
$\left(\dfrac{1}{3}\right)^4\left(y^{\frac{1}{3}}\right)^4 ⋅ (2)^2(x^2)^2(y)^2$
$\left(\dfrac{1}{81}\right)\left(y^{\frac{1}{3} ⋅ 4}\right)(4)(x^{2⋅2})(y^2)$
$\left(\dfrac{1}{81}\right)\left(y^{\frac{4}{3}}\right)(4)(x^4)(y^2)$
$\dfrac{4}{81}x^4y^{\frac{4}{3} + 2}$
$\dfrac{4}{81}x^4y^{\frac{4}{3} + \frac{6}{3}}$
$\dfrac{4}{81}x^4y^{\frac{10}{3}}$
Question 3 |
The expression $(x + y) [z − (x − y)]$ is equivalent to which of the following?
$xz − x^2 + 2xy + y^2$ | |
$2xz + x^2 − yz + y^2$ | |
$xz − x^2 + yz + y^2$ | |
$xz + x^2 − yz − y^2$ | |
$xyz + y^2 − xy + yz + y^2$ |
Question 3 Explanation:
The correct answer is (C). Recall order of operations and the distributive property to answer this question.
$(x + y)[z - (x - y)]$
$(x + y)[z - x + y]$
$(x)(z) + (x)(-x) + (x)(y) $ $ + (y)(z) + (y)(-x) + (y)(y)$
$xz - x^2 + xy + yz - xy + y^2$
$xz - x^2 + yz + y^2$
$(x + y)[z - (x - y)]$
$(x + y)[z - x + y]$
$(x)(z) + (x)(-x) + (x)(y) $ $ + (y)(z) + (y)(-x) + (y)(y)$
$xz - x^2 + xy + yz - xy + y^2$
$xz - x^2 + yz + y^2$
Question 4 |
There are 32 marbles in a jar: 14 blue, 10 red, 5 green, and 3 yellow. Sally pulls one marble, randomly, from the jar. Without replacing the marble, she pulls another marble. What is the probability that both marbles will be red?
$\dfrac{40}{426}$ | |
$\dfrac{41}{456}$ | |
$\dfrac{43}{476}$ | |
$\dfrac{44}{476}$ | |
$\dfrac{45}{496}$ |
Question 4 Explanation:
The correct answer is (E). The probability of selecting a red marble on the first draw is $\frac{10}{32}$ because there are 10 red marbles and 32 total marbles.
After removing the first red marble there are now 9 red marbles and 31 total marbles left so $\frac{9}{31}$ chance of selecting the second red marble.
To find the probability of both events occurring, we multiply the probabilities:
$\left(\frac{10}{32}\right)\left(\frac{9}{31}\right) = \left(\frac{5}{16}\right)\left(\frac{9}{31}\right) $ $ = \frac{45}{496}$
After removing the first red marble there are now 9 red marbles and 31 total marbles left so $\frac{9}{31}$ chance of selecting the second red marble.
To find the probability of both events occurring, we multiply the probabilities:
$\left(\frac{10}{32}\right)\left(\frac{9}{31}\right) = \left(\frac{5}{16}\right)\left(\frac{9}{31}\right) $ $ = \frac{45}{496}$
Question 5 |
If $x+y=7$ $\text{and}$ $x-y=3$, what is $x^2-y^2= \; ?$
$9$ | |
$21$ | |
$25$ | |
$36$ | |
$40$ |
Question 5 Explanation:
The correct answer is (B). We can solve this problem using 2 different approaches:
Approach 1 – Solving a system of equations:
$x + y = 7$
$x - y = 3$
Using the "elimination" method, we have:
$ \begin{array}{lc} & x + y = 7 \\ + & x - y = 3 \\ \hline & 2x + 0 = 10 \\ \end{array} $
$2x = 10$
$x = 5$
Substituting $x = 5$ into one of the original equations:
$x + y = 7$
$5 + y = 7$
$y = 2$
Substituting $x = 5$ and $y = 2$ into $x^2 - y^2$:
$x^2 - y^2 = (5)^2 - (2)^2 = 25 - 4 = 21$
Approach 2 – Recognize that $x^2 - y^2 = (x + y)(x - y)$:
Since $x^2 - y^2$ is a difference of two squares, it can be factored as:
$x^2 - y^2 = (x + y)(x - y)$
We are given $x + y = 7$ and $x - y = 3$.
Substituting into our factored equation gives:
$x^2 - y^2 = (7)(3)$
$x^2 - y^2 = 21$
Approach 1 – Solving a system of equations:
$x + y = 7$
$x - y = 3$
Using the "elimination" method, we have:
$ \begin{array}{lc} & x + y = 7 \\ + & x - y = 3 \\ \hline & 2x + 0 = 10 \\ \end{array} $
$2x = 10$
$x = 5$
Substituting $x = 5$ into one of the original equations:
$x + y = 7$
$5 + y = 7$
$y = 2$
Substituting $x = 5$ and $y = 2$ into $x^2 - y^2$:
$x^2 - y^2 = (5)^2 - (2)^2 = 25 - 4 = 21$
Approach 2 – Recognize that $x^2 - y^2 = (x + y)(x - y)$:
Since $x^2 - y^2$ is a difference of two squares, it can be factored as:
$x^2 - y^2 = (x + y)(x - y)$
We are given $x + y = 7$ and $x - y = 3$.
Substituting into our factored equation gives:
$x^2 - y^2 = (7)(3)$
$x^2 - y^2 = 21$
Question 6 |
The circumference of a large wedding cake is 60 inches. If the cake is divided evenly into 12 slices, what is the length of the arc, in inches, made by 5 combined slices?
$12$ | |
$13$ | |
$15$ | |
$20$ | |
$25$ |
Question 6 Explanation:
The correct answer (E). Recall that the circumference is the distance around a circle. If the cake is divided into 12 equal slices, the arc length of each slice will be:
$\dfrac{60\text{ inches}}{12\text{ slices}} = 5 \dfrac{\text{inches}}{\text{slice}}$
Summing 5 of these slices, we have:
$5 \text{ slices } \ast 5 \dfrac{\text{inches}}{\text{slice}} = 25 \text{ inches}$
$\dfrac{60\text{ inches}}{12\text{ slices}} = 5 \dfrac{\text{inches}}{\text{slice}}$
Summing 5 of these slices, we have:
$5 \text{ slices } \ast 5 \dfrac{\text{inches}}{\text{slice}} = 25 \text{ inches}$
Question 7 |
A rectangle has an area of $507 \text{ cm}^2$. One side of the rectangle has a length of $39 \text{ cm}$. What is the length of the diagonal of the rectangle in cm (rounded to the nearest tenth)?
$50.9$ | |
$41.1$ | |
$49.0$ | |
$55.7$ | |
$34.8$ |
Question 7 Explanation:
The correct answer is (B). We know that the area of a rectangle is its length times its width:
$A_{\text{rect }} = \text{length } * \text{ width}$
$507 = 39 * \text{ width}$
(Note: It does not matter whether we treat the 39 cm as the length or the width in solving this problem.)
$\text{width} = 13 \text{cm}$
To find the length of the diagonal, we use the Pythagorean Theorem:
$\text{diagonal}^2 = \text{ length}^2 + \text{ width}^2$
$\text{diagonal}^2 = 39^2 + 13^2$
$\text{diagonal}^2 = 1690$
$\text{diagonal } = \sqrt{1690}$
$\text{diagonal } \approx41.1 \text{ cm}$
Notice that answer choice (E) is impossible since the diagonal of a rectangle is always greater than its length and its width.
$A_{\text{rect }} = \text{length } * \text{ width}$
$507 = 39 * \text{ width}$
(Note: It does not matter whether we treat the 39 cm as the length or the width in solving this problem.)
$\text{width} = 13 \text{cm}$
To find the length of the diagonal, we use the Pythagorean Theorem:
$\text{diagonal}^2 = \text{ length}^2 + \text{ width}^2$
$\text{diagonal}^2 = 39^2 + 13^2$
$\text{diagonal}^2 = 1690$
$\text{diagonal } = \sqrt{1690}$
$\text{diagonal } \approx41.1 \text{ cm}$
Notice that answer choice (E) is impossible since the diagonal of a rectangle is always greater than its length and its width.
Question 8 |
If $f(x) = x^2 + 2x + 2$, what is $f(x + h)?$
$2x^2 + 4hx + h^2 − 2x − 2h$ | |
$x + h^2 + 2xh + 2 + h$ | |
$x^2 + 2x + 2xh + 2h + h^2 + 2$ | |
$x^2 + 4xh + 4h^2 + 2x$ | |
$2x^2 + 2xh + 2h^2 + 2x + 2$ |
Question 8 Explanation:
The correct answer is (C). To solve this problem we will substitute $(x + h)$ for every $x$ in our function $f(x)$:
$f(x + h) = $ $ (x + h)^2 + 2(x +h) + 2$
$f(x + h) = $ $ (x + h)(x + h) $ $ + \, 2(x +h) + 2$
$f(x + h) = $ $ (x^2 + xh + xh + h^2) $ $ + \, (2x +2h) + 2$
$f(x + h) = $ $ x^2 + 2xh + h^2 $ $ + \, 2x + 2h + 2$
Rearranging, we have:
$f(x + h) = $ $ x^2 + 2x + 2xh $ $ + \, 2h + h^2 + 2$
$f(x + h) = $ $ (x + h)^2 + 2(x +h) + 2$
$f(x + h) = $ $ (x + h)(x + h) $ $ + \, 2(x +h) + 2$
$f(x + h) = $ $ (x^2 + xh + xh + h^2) $ $ + \, (2x +2h) + 2$
$f(x + h) = $ $ x^2 + 2xh + h^2 $ $ + \, 2x + 2h + 2$
Rearranging, we have:
$f(x + h) = $ $ x^2 + 2x + 2xh $ $ + \, 2h + h^2 + 2$
Question 9 |
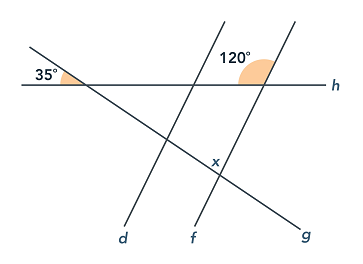
In the figure above, lines $d$ and $f$ are parallel and the angle measures are as given. What is the value of $x$?
$35^\text{o}$ | |
$60^\text{o}$ | |
$85^\text{o}$ | |
$100^\text{o}$ | |
$120^\text{o}$ |
Question 9 Explanation:
The correct answer is (C). Since vertical angles are congruent, the angle vertical to the 35-degree angle also has a measure of 35 degrees. The supplement of the 120-degree angle has a measure of 60 degrees, so we then have a triangle with angles measuring 35, 60, and $x$ degrees, as shown in the figure provided. Since the angles of a triangle add to 180 degrees:
$35 + 60 + x = 180$
$x = 180 − 35 − 60$
$x = 85^\text{o}$
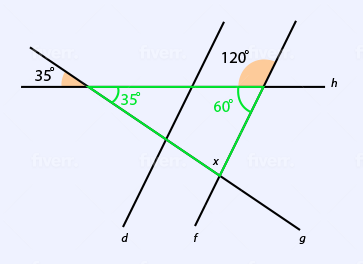
$35 + 60 + x = 180$
$x = 180 − 35 − 60$
$x = 85^\text{o}$

Question 10 |
Which of the following represents the equation of the line that passes through the point $(2, 3)$ with a slope of $−\frac{1}{3}$?
$y = 2x + 4$ | |
$y = 4x + 2$ | |
$y = −\dfrac{1}{3}x + \dfrac{11}{3}$ | |
$y = −3x + \dfrac{11}{3}$ | |
$y = −\dfrac{2}{3}x + \dfrac{11}{3}$ |
Question 10 Explanation:
The correct answer is (C). Recall that when provided with a point and the slope of a line, we can use point-slope formula to write an equation for the line. The point slope formula is $y − y_1 = m(x − x_1)$ where $(x_1, y_1)$ is the point provided and m is the slope. Plug in the point and slope provided and solve for $y$:
$y − 3 = −\dfrac{1}{3} (x − 2)$
$y - 3 = -\dfrac{1}{3}x + \dfrac{2}{3}$
$y = -\dfrac{1}{3}x + \dfrac{2}{3} + 3$
$y = -\dfrac{1}{3}x + \dfrac{2}{3} + \dfrac{9}{3}$
$y = −\dfrac{1}{3}x + \dfrac{11}{3}$
$y − 3 = −\dfrac{1}{3} (x − 2)$
$y - 3 = -\dfrac{1}{3}x + \dfrac{2}{3}$
$y = -\dfrac{1}{3}x + \dfrac{2}{3} + 3$
$y = -\dfrac{1}{3}x + \dfrac{2}{3} + \dfrac{9}{3}$
$y = −\dfrac{1}{3}x + \dfrac{11}{3}$
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 10 questions to complete.
|
List |
Next Practice Test:
ACT Math Practice Test 6 >>
More Practice Tests:
ACT Math – Main Menu >>
ACT Science Practice >>
ACT English Practice >>
ACT Reading Practice >>
