Here is Part A of our AP Calculus AB free response questions. This is the first FRQ section of our AP Calculus AB Practice Exam. After you write down your solutions you can check your answers here. A graphing calculator is required for both of these problems.
Question #1
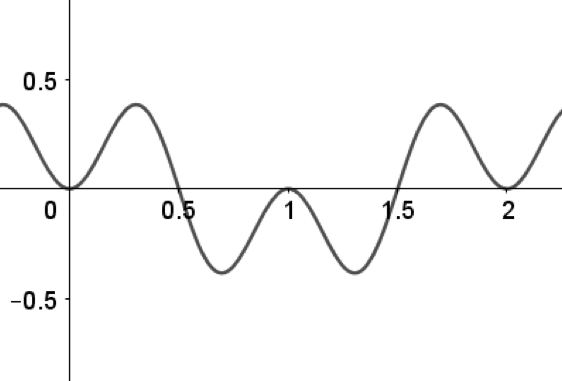
Above is the graph of $f'(x) = \sin^2(πx) \cos(πx).$
(a) Identify the function for $f(x)$.
(b) Identify $1$ local maximum and $1$ local minimum for $f(x)$. Give evidence for each extremum.
(c) Identify $1$ point of inflection with evidence on $0 ≤ x ≤ 2$.
(d) Identify where $f(x)$ is increasing and decreasing on $0 ≤ x ≤ 2$ with a reason for each answer.
Question #2
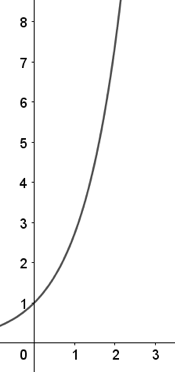
Above is the curve for $y = e^x$ restricted by the $y$-axis and $y = e^3$.
(a) Find the volume formed by revolving the curve around the y-axis.
(b) The revolved shape forms the shape of a canister used to store water. The volume calculated in part (a) is a measurement in gallons. Water flows into the canister at $2$ gallons per minute. What is the rate of change of the radius of the water in the canister when there are $217$ gallons in the canister?
Hint: $\displaystyle\int xe^x = xe^x − e^x + C$
