Here are the answers to Part A of our AP Calculus AB free response questions.
Question #1
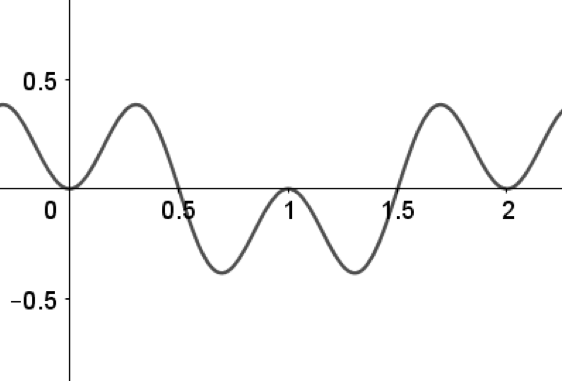
Above is the graph of $f'(x) = \sin^2(πx) \cos(πx).$
(a) Identify the function for $f(x)$.
(b) Identify $1$ local maximum and $1$ local minimum for $f(x)$. Give evidence for each extremum.
(c) Identify $1$ point of inflection with evidence on $0 ≤ x ≤ 2$.
(d) Identify where $f(x)$ is increasing and decreasing on $0 ≤ x ≤ 2$ with a reason for each answer.
Answer to Question #1:
(a)
$\displaystyle\int f'(x) dx = f(x)$
$\displaystyle\int \sin^2(πx)\cos(πx)dx = \dfrac{1}{3π} \sin^3(πx) + C$
$f(0) = \dfrac{1}{3π} \sin^3(0) + C = 1$,$C = 1$
$f(x) = \dfrac{1}{3π} \sin^3(πx) + 1$
(b)
Local Maximum: $(0.5, 0.106)$
$f'(x)$ changes from positive to negative about $x = 0.5$
Local Minimum: $(1.5,−0.106)$
$f'(x)$ changes from negative to positive about $x = 1.5$
(c)
Point of Inflection: $(0.304, 0.058)$, $(0.696, 0.058)$, $(1,0)$, $(1.304, −0.058)$, $(1.696, −0.058)$, or $(2, 0)$
$f'(x)$ has horizontal tangent lines at those points or $f”(x) = 0$ at specified $x$-value.
(d)
Increasing on $(0,0.5)U(1.5,2)$ as $f'(x)$ is positive on that domain.
Decreasing on $(0.5,1)U(1,1.5)$ as $f'(x)$ is negative on that domain.
Question #2
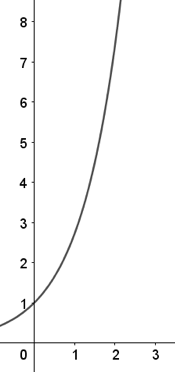
Above is the curve for $y = e^x$ restricted by the $y$-axis and $y = e^3$.
(a) Find the volume formed by revolving the curve around the y-axis.
(b) The revolved shape forms the shape of a canister used to store water. The volume calculated in part (a) is a measurement in gallons. Water flows into the canister at $2$ gallons per minute. What is the rate of change of the radius of the water in the canister when there are $217$ gallons in the canister?
Hint: $\displaystyle\int xe^x = xe^x − e^x + C$
Answer to Question #2:
(a)
$V = 2π\displaystyle\int_0^3 x(e^3 − e^x)dx$
$V = 5πe^3 – 2π ≈ 309.220$
(b)
$V = 2π \displaystyle\int_0^{x_1} x(e^3 − e^x)dx$
$\dfrac{dV}{dt}$ $= \dfrac{d(2π \displaystyle\int_0^{x_1} x(e^3 − e^x)dx)}{dt}$
$= 2πx_1 (e^3 − e^{x_1}) \cdot \dfrac{dx}{dt} = 2$
$V = 217 = 2π\displaystyle\int_0^{x_1}x(e^3 − e^x)dx$
$= πx_1^2 e^3 − 2πx_1 e^{x_1} + 2πe^{x_1} − 2π$
$x_1 = 2.109$
Radius $= x_1 = 2.109$
$\dfrac{dx}{dt}$ $= \dfrac{2}{2πx_1(e^3 − e^{x_1})}$ $= 0.013$ units/minute
