Here are the answers to Part B of our AP Calculus AB free response questions.
Question #3
Consider the differential equation $\dfrac{dy}{dx} = x^3 − 2y^2$.
(a) Sketch the slope field for the differential equation on the graph provided below.
(b) Find $\dfrac{d^2y}{dx^2}$ in terms of $x$ and $y$. Determine the concavity of the possible solution curves to the differential equation in the second quadrant based on your answer.
(c) Given the differential equation $\dfrac{dy}{dx} = 2x^3y^2$, solve for $y$ in terms of $x$.
Answer to Question #3:
(a)

(b)
$\dfrac{d^2 y}{dx^2}$ $= 3x^2 – 4y(x^3 – 2y^2)$
$= 3x^2 – 4x^3y + 8y^3$
In the second quadrant, $x < 0$, and $y > 0$. Therefore $3x^2 – 4x^3y + 8y^3 > 0$ in quadrant II. Solution curves are all concave up.
(c)
$\dfrac{1}{y^2}dy = 2x^3 dx$
$-y^{-1} = \dfrac{1}{2} x^4 + C$
$y = \dfrac{1}{-\frac{1}{2}x^4 + C}$
Question #4
Tim and John get in an argument over the limit below.
$\lim\limits_{x\to 0} \dfrac{2x}{\cos(x)}$
Tim says the limit exists while John says the limit does not exist.
(a) Identify derivative of $x^2$ using the limit definition.
(b) Identify the derivative of $\sin(x)$ using the limit definition.
(c) Identify $\lim\limits_{x\to 0} \dfrac{2x}{\sin(x)}$
(d) Who is correct? Give a reason with your answer.
Answer to Question #4:
(a)
$\dfrac{d(x^2)}{dx}$ $= \lim\limits_{∆h\to 0} \dfrac{(x + ∆h)^2 − x^2}{∆h}$
$= \lim\limits_{∆h\to 0} \dfrac{2x∆h + ∆h^2}{∆h}$
$= \lim\limits_{∆h\to 0} 2x + ∆h = 2x$
(b)
$\dfrac{d(\sin(x))}{dx}$ $= \lim\limits_{∆h\to 0} \dfrac{\sin(x + ∆h) − \sin(x)}{∆h}$
$= \lim\limits_{∆h\to 0} \dfrac{\sin(x)\cos(∆h) + \cos(x)\sin(∆h) − \sin(x)}{∆h}$
$= \lim\limits_{∆h\to 0} (−\sin(x))\left(\dfrac{1 − cos(∆h)}{∆h}\right)$ $+ \lim\limits_{∆h\to 0} \cos(x) \left(\dfrac{\sin(∆h)}{∆h}\right)$
$= \lim\limits_{∆h\to 0} \dfrac{1 − \cos(∆h)}{∆h}$ $= 0,\lim\limits_{∆h\to 0} \dfrac{\sin(∆h)}{∆h}$ $= 1$
$\dfrac{d(\sin(x))}{dx} = \cos(x)$
(c)
$\lim\limits_{x\to 0} \dfrac{x^2}{\sin(x)} \to \dfrac{0}{0}$
$\lim\limits_{x\to 0} \dfrac{2x}{\cos(x)}$ $= \dfrac{0}{1} = 0$
(d)
Tim is correct, as the limit is equal to $0$.
Question #5
A particle moves along the $x$-axis over time, $t$, in seconds by the equation below. $t ≥ 0$
$s(t) = t^3 − 6t^2 + 9t − 18$
(a) Find the velocity and acceleration functions for the particle.
(b) When is the particle at rest?
(c) When is the particle moving in the forward direction?
(d) When is the particle increasing in speed?
(e) When is the particle moving the fastest in the backwards direction?
(f) Find the total distance travelled by the particle after $5$ seconds.
Answer to Question #5:
(a)
$v(t) = 3t^2 − 12t + 9$
$a(t) = 6t – 12 = 6(t − 2)$
(b)
$v(t) = 0 = 3(t − 3)(t − 1)$
$t = 3$, $t = 1$
(c)
$v(t)$ is positive when particle moves forward
$0 ≤ t< 1$, $3 < t < \infty$
(d)
Both $v(t)$ and $a(t)$ must have same sign.
$1 < t < 2$ Both negative
$3 < t < \infty$ Both positive
(e)
$a(t) = v'(t)$
$a(t) = 0$,$t = 2$ Critical Point
$a(t)$ changes from negative to positive about $t = 2$, therefore $t = 2$ is a local minimum on $v(t)$.
(f)
Distance $= \displaystyle\int_0^5 |v(t)|dt$
$\displaystyle\int_0^5 v(t)dt − 2\displaystyle\int_1^3v(t)dt = 28$ units
Question #6
Use the table below to answer all parts of the question. Assume that $f(x)$ is continuous and differentiable on all $x$. $f'(x) = 0$ only at one value for all $x$.
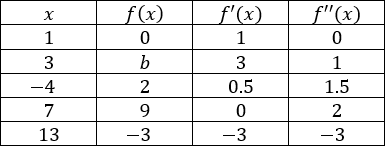
(a) Identify the critical point(s) and point(s) of inflection for $f(x)$. Give a reason for each answer.
(b) Identify any local extrema for $f(x)$, stating reasons for each extremum identified.
(c) Using a tangent line approximation from $f(1)$, identify an appropriate approximation for b.
(d) How many roots does $f(x)$ have on $−4 ≤ x ≤ 13$? State a reason for your answer.
Answer to Question #6:
(a)
Critical Point: $(7,9)$
$f'(7) = 0$
Point of Inflection: $(1,0)$
$f”(1) = 0$
(b)
Local maximum at $x = 7$ as $f'(x)$ changes from positive to negative about $x = 7$.
(c)
$f'(1) = 1$, $f(1) = 0$
$y − 0 = (1)(x − 1)$
$y ≈ (3 − 1) = 2$
$b ≈ 2$
(d)
$f(x)$ has at least two roots on $−4 ≤ x ≤ 13$ due to intermediate value theorem, which guarantees the existence of one root between $x = 7$ and $x = 13$ as $f(x)$ is continuous on the domain and $f(x)$ changes from positive to negative. $x = 1$ is a root as well, as $f(1) = 0$.
