This is Part A of the multiple choice section of our free AP Calculus AB practice exam. There are a total of 30 test questions which must be answered within 60 minutes. A calculator may not be used on this part of the AP Calculus multiple choice test.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
Evaluate the derivative of the following function.
$f(x) = \ln(2x) + 6$
$f'(x) = \dfrac{1}{2x}$ | |
$f'(x) = \dfrac{1}{x} + 6x$ | |
$f'(x) = \dfrac{1}{x}$ | |
$f'(x) = \ln(2x)$ |
Question 1 Explanation:
The correct answer is (C). Recall the derivative rule for natural log functions.
$\dfrac{d}{du} \ln(u) = \dfrac{1}{u} \cdot du$
Then, the derivative of the function is as follows.
$f(x) = \dfrac{1}{x}$
$\dfrac{d}{du} \ln(u) = \dfrac{1}{u} \cdot du$
Then, the derivative of the function is as follows.
$f(x) = \dfrac{1}{x}$
Question 2 |
Identify the equation of the line tangent to the point at $x = 0$ for the function below.
$f(x) = 4\arctan(2x)$
$y − \dfrac{π}{4} = 8x$ | |
$y = 8x$ | |
$y − \dfrac{π}{2} = 4x$ | |
$y = 4x$ |
Question 2 Explanation:
The correct answer is (B). We must first identify the slope of the tangent line at $x = 0$. This slope is equivalent to the value of the derivative at $x = 0$. Don’t forget the rules for derivation of inverse trigonometric functions.
$f'(x) = 4(\dfrac{1}{1 + (2x)^2})\cdot 2$ $= \dfrac{8}{1 + (2x)^2}$
$f'(0) = \dfrac{8}{1+(0)^2} = 8$
It is important not to forget that the equation for the tangent line in point slope form takes the general form below, where $(x_1, y_1 )$ is a given or known point on the function and $m$ is the slope of the line.
$y − y_1 = m(x − x_1)$
Thus, we need a point on the function. However, for the tangent line, we need more than just any point on the function, but actually the specific point on the function that the line is tangent to. We know that the tangent line at $x = 0$ is tangent to only the point on the function where $x = 0$. Therefore, we must identify the point on the function where $x = 0$ to find the known point for the point-slope formula. We can identify the function value at $x = 0$ by plugging in this value of $x$.
$f(0) = 4 \arctan(0)$ $= 4(0) = 0$
Therefore, the point $(0, 0)$ is on the tangent line. Thus, the equation of the tangent line is of the form below.
$y − 0 = 8(x − 0)$
$y = 8x$
$f'(x) = 4(\dfrac{1}{1 + (2x)^2})\cdot 2$ $= \dfrac{8}{1 + (2x)^2}$
$f'(0) = \dfrac{8}{1+(0)^2} = 8$
It is important not to forget that the equation for the tangent line in point slope form takes the general form below, where $(x_1, y_1 )$ is a given or known point on the function and $m$ is the slope of the line.
$y − y_1 = m(x − x_1)$
Thus, we need a point on the function. However, for the tangent line, we need more than just any point on the function, but actually the specific point on the function that the line is tangent to. We know that the tangent line at $x = 0$ is tangent to only the point on the function where $x = 0$. Therefore, we must identify the point on the function where $x = 0$ to find the known point for the point-slope formula. We can identify the function value at $x = 0$ by plugging in this value of $x$.
$f(0) = 4 \arctan(0)$ $= 4(0) = 0$
Therefore, the point $(0, 0)$ is on the tangent line. Thus, the equation of the tangent line is of the form below.
$y − 0 = 8(x − 0)$
$y = 8x$
Question 3 |
$\displaystyle\int [\tan(x) + sec^2(x)]dx =$
$− \ln |\cos(x)| − \tan(x) + C$ | |
$\ln |\sec(x)| − \tan(x) + C$ | |
$\ln |\sec(x)| + \tan(x) + C$ | |
$−\ln |\cos(x)| + \tan(x) + C$ |
Question 3 Explanation:
The correct answer is (D). The anti-derivative of $\tan(x)$ is $−\ln|\cos(x)| + C$.
The anti-derivative of $\sec^2(x)$ is $\tan(x) + C$.
The sum of these two integrals is $−\ln|\cos(x)| + \tan(x) + C$.
The anti-derivative of $\sec^2(x)$ is $\tan(x) + C$.
The sum of these two integrals is $−\ln|\cos(x)| + \tan(x) + C$.
Question 4 |
$\displaystyle\int_0^1 \dfrac{4}{1 + x^2}dx =$
$0$ | |
$1$ | |
$\dfrac{π}{2}$ | |
$π$ |
Question 4 Explanation:
The correct answer is (D). Factoring out the $4$ from the numerator, we see that the integral is in the form $\frac{du}{a^2 + u^2}$. Ignoring the constant of integration, the anti-derivative is:
$4\arctan(x)$
Using the first fundamental theorem to evaluate the definite integral:
$4\arctan(1) − 4\arctan(0)$ $= 4\left(\dfrac{π}{4}\right) − 4(0) = π$
$4\arctan(x)$
Using the first fundamental theorem to evaluate the definite integral:
$4\arctan(1) − 4\arctan(0)$ $= 4\left(\dfrac{π}{4}\right) − 4(0) = π$
Question 5 |
Identify the time where the position function below reaches its minimum velocity, $t ≥ 0$.
$s(t) = t^4 − 3t^3 − 6t^2 + 27t$
$t = 2$ | |
$t = \dfrac{9}{4}$ | |
$t = 3$ | |
$t = −\dfrac{1}{2}$ |
Question 5 Explanation:
The correct answer is (A). To find the minimum velocity, it will first be beneficial to find the velocity function.
$v(t )= s'(t) =$ $4t^3 − 9t^2 − 12t + 27$
Then, we know that we can find the extrema of functions by finding their critical points. Thus, we must find the critical points of the velocity function. To do this, we must take the derivative of the velocity function.
$v'(t) = 12t^2 − 18t − 12$
We can then set this equation equal to zero to determine the critical points.
$12t^2 − 18t − 12 = 0$
$t = 2$, $t = −\dfrac{1}{2}$
However, we were given that $t ≥ 0$, which implies that $t = 2$ is the only critical point. We can then determine what type of extrema exists at this critical point using the first derivative test.
We can then create a sign pattern for $v'(t)$ to determine the type of extrema.
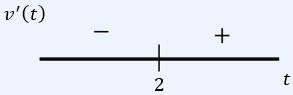
It is clear from the sign pattern that $t = 2$ is a relative minimum for the velocity function.
$v(t )= s'(t) =$ $4t^3 − 9t^2 − 12t + 27$
Then, we know that we can find the extrema of functions by finding their critical points. Thus, we must find the critical points of the velocity function. To do this, we must take the derivative of the velocity function.
$v'(t) = 12t^2 − 18t − 12$
We can then set this equation equal to zero to determine the critical points.
$12t^2 − 18t − 12 = 0$
$t = 2$, $t = −\dfrac{1}{2}$
However, we were given that $t ≥ 0$, which implies that $t = 2$ is the only critical point. We can then determine what type of extrema exists at this critical point using the first derivative test.
We can then create a sign pattern for $v'(t)$ to determine the type of extrema.
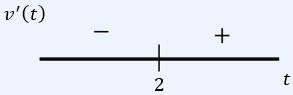
It is clear from the sign pattern that $t = 2$ is a relative minimum for the velocity function.
Question 6 |
A plane in horizontal (level) flight is travelling at a speed of 500 feet
per second. The plane passes 100 feet directly above the eyes of a boy who
watches the plane as it flies away from him.
At what rate is the angle of the boy's eyes changing when the plane has travelled 100 feet horizontally from the point where it passed directly overhead?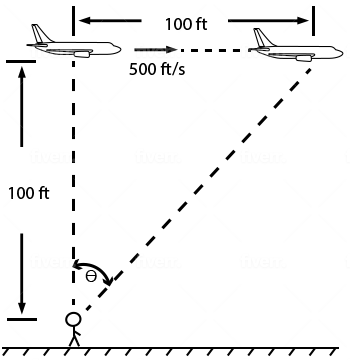
At what rate is the angle of the boy's eyes changing when the plane has travelled 100 feet horizontally from the point where it passed directly overhead?

$\dfrac{1}{26}$ $\text{radians}$ $\text{per}$ $\text{second}$ | |
$\dfrac{5}{2}$ $\text{radians}$ $\text{per}$ $\text{second}$ | |
$\dfrac{1}{200}$ $\text{radians}$ $\text{per}$ $\text{second}$ | |
$\dfrac{50,000}{(20,000)^{\frac{1}{2}}}$ $\text{feet}$ $\text{per}$ $\text{second}$ |
Question 6 Explanation:
The correct answer is (B). We shall first construct a diagram of the described event to aid in solving the problem.
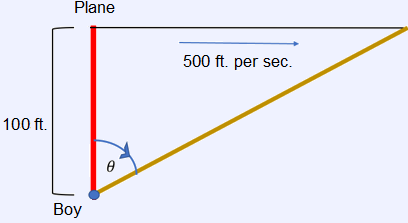
It is clear from the diagram that the relationship for this problem is related to triangle properties. We can relate the angle of the boy’s eyes with the plane through trigonometric functions. Let $t$ represent the time that the boy has been watching the plane since it passed over his head.
$\tan(θ) = \dfrac{500t}{100}$
We can then derive this relationship to relate the planes rate of travel with the change in angle.
$sec^2(θ) \cdot \dfrac{dθ}{dt}$ $= 5 \dfrac{dt}{dt} = 5$
Then, we can find $θ$, as it is given the plane is $100$ feet away from him. This means that $\frac{1}{5}$ of a second has passed.
$tan(θ) = \dfrac{100}{100} = 1$
$θ = tan^{−1}(1) = \dfrac{π}{4}$
Then, we can plug this value into the derived equation to find the rate of change of the angle.
$\sec^2 \left(\dfrac{π}{4}\right) \cdot \dfrac{dθ}{dt} = 5$
$\dfrac{dθ}{dt} = \dfrac{5}{sec^2 \left(\frac{π}{4}\right)}$ $ = \dfrac{5}{\left(\frac{2}{\sqrt{2}}\right)^2} = \dfrac{5}{2}$ $\text{radians}$ $\text{per}$ $\text{second}$
Don’t forget to add units. Be careful about the units of the angle, as it must be in radians, not degrees.

It is clear from the diagram that the relationship for this problem is related to triangle properties. We can relate the angle of the boy’s eyes with the plane through trigonometric functions. Let $t$ represent the time that the boy has been watching the plane since it passed over his head.
$\tan(θ) = \dfrac{500t}{100}$
We can then derive this relationship to relate the planes rate of travel with the change in angle.
$sec^2(θ) \cdot \dfrac{dθ}{dt}$ $= 5 \dfrac{dt}{dt} = 5$
Then, we can find $θ$, as it is given the plane is $100$ feet away from him. This means that $\frac{1}{5}$ of a second has passed.
$tan(θ) = \dfrac{100}{100} = 1$
$θ = tan^{−1}(1) = \dfrac{π}{4}$
Then, we can plug this value into the derived equation to find the rate of change of the angle.
$\sec^2 \left(\dfrac{π}{4}\right) \cdot \dfrac{dθ}{dt} = 5$
$\dfrac{dθ}{dt} = \dfrac{5}{sec^2 \left(\frac{π}{4}\right)}$ $ = \dfrac{5}{\left(\frac{2}{\sqrt{2}}\right)^2} = \dfrac{5}{2}$ $\text{radians}$ $\text{per}$ $\text{second}$
Don’t forget to add units. Be careful about the units of the angle, as it must be in radians, not degrees.
Question 7 |
$\dfrac{d}{dx} \left[\displaystyle\int_0^{x^2 + 7x} \sin(t) \cos(t)dt\right] =$
$\sin(x^2 + 7x) \cdot \cos(x^2 + 7x)$ | |
$\dfrac{1}{2}\sin(x^2 + 7x)$ | |
$\dfrac{1}{2}\sin(2x^2 + 14x) \cdot (2x + 7)$ | |
$\dfrac{1}{2}\sin(2x^2 + 14x) \cdot \left(\dfrac{1}{3}x^3 + \dfrac{7}{2}x^2\right)$ |
Question 7 Explanation:
The correct answer is (C). The derivative of the upper bound is $2x + 7$. Applying the second fundamental theorem gives:
$(2x + 7)\sin(x^2 + 7x)\cos(x^2 + 7x)$
Using the double angle identity gives
$\dfrac{1}{2} (2x + 7) \sin(2x^2 + 14x)$.
$(2x + 7)\sin(x^2 + 7x)\cos(x^2 + 7x)$
Using the double angle identity gives
$\dfrac{1}{2} (2x + 7) \sin(2x^2 + 14x)$.
Question 8 |
$\lim\limits_{x\to \infty} \dfrac{x^3}{\ln(x)} =$
$− \infty$ | |
$3x^3$ | |
$3$ | |
$\text{DNE}$ |
Question 8 Explanation:
The correct answer is (D). The limit evaluates to $\frac{\infty}{\infty}$ through direct substitution, which is one of the indeterminate forms which justifies the use of L’Hôpital’s rule.
$\lim\limits_{x\to \infty} \dfrac{x^3}{\ln(x)}$ $= \lim\limits_{x\to \infty} \dfrac{3x^2}{\frac{1}{x}}$ $= \lim\limits_{x\to \infty} 3x^3 = \infty$
Therefore, the limit does not exist.
$\lim\limits_{x\to \infty} \dfrac{x^3}{\ln(x)}$ $= \lim\limits_{x\to \infty} \dfrac{3x^2}{\frac{1}{x}}$ $= \lim\limits_{x\to \infty} 3x^3 = \infty$
Therefore, the limit does not exist.
Question 9 |
$\displaystyle\int \dfrac{2 + 2x}{1 − x^2}dx =$
$− 2\ln |2 + x| + C$ | |
$2\ln |1 − x| + C$ | |
$− 2\ln |1 − x| + C$ | |
$2\ln |2 + x| + C$ |
Question 9 Explanation:
The correct answer is (C). Factoring the numerator and denominator of the integrand gives:
$\displaystyle\int \dfrac{2(1 + x)}{(1 + x)(1 − x)} dx$
Canceling like terms:
$\displaystyle\int \dfrac{2}{1 − x}dx$
Taking the $2$ out of the integral and multiplying by $−1$ gives:
$−2 \displaystyle\int \dfrac{−1}{(1 −x)} dx$
This is an integral in the form $\frac{u'}{u}$. So, the following is the correct evaluation:
$−2 \ln|1 − x| + C$
$\displaystyle\int \dfrac{2(1 + x)}{(1 + x)(1 − x)} dx$
Canceling like terms:
$\displaystyle\int \dfrac{2}{1 − x}dx$
Taking the $2$ out of the integral and multiplying by $−1$ gives:
$−2 \displaystyle\int \dfrac{−1}{(1 −x)} dx$
This is an integral in the form $\frac{u'}{u}$. So, the following is the correct evaluation:
$−2 \ln|1 − x| + C$
Question 10 |
Use the following table to calculate the trapezoidal sum of the area under the curve on the interval $[0, 4], (Δx = 1)$.
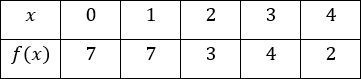

$\dfrac{37}{4}$ | |
$16$ | |
$\dfrac{37}{2}$ | |
$21$ |
Question 10 Explanation:
The correct answer is (C). Applying the formula for the trapezoidal sum:
$\dfrac{1}{2}[7 + 2(7) + 2(3) + 2(4) + 2]$
$= \dfrac{1}{2}(37) = \dfrac{37}{2}$
$\dfrac{1}{2}[7 + 2(7) + 2(3) + 2(4) + 2]$
$= \dfrac{1}{2}(37) = \dfrac{37}{2}$
Question 11 |
Which of the following answer choices is a solution to the differential equation below?
$y''' − 6y'' + 11y' − 6y = 0$
$y = e^{−x}$ | |
$y = e^{4x}$ | |
$y = e^{−3x}$ | |
$y = e^{3x}$ |
Question 11 Explanation:
The correct answer is (D). The first three derivatives of $e^{3x}$ are:
$y = e^{3x}$
$y' = 3e^{3x}$
$y'' = 9e^{3x}$
$y''' = 27e^{3x}$
Plugging in the values above into the differential equation:
$27e^{3x} − 6(9e^{3x}) + 11(3e^{3x}) − 6(e^{3x})$
$= e^{3x} (27 − 54 + 33 − 6)$
$= 0(e^{3x}) = 0$
Since the result is $0$, $y = e^{3x}$ is a valid solution to the differential equation.
$y = e^{3x}$
$y' = 3e^{3x}$
$y'' = 9e^{3x}$
$y''' = 27e^{3x}$
Plugging in the values above into the differential equation:
$27e^{3x} − 6(9e^{3x}) + 11(3e^{3x}) − 6(e^{3x})$
$= e^{3x} (27 − 54 + 33 − 6)$
$= 0(e^{3x}) = 0$
Since the result is $0$, $y = e^{3x}$ is a valid solution to the differential equation.
Question 12 |
Determine the average value under the function
$f(x) = 3\cos(x)$ on the interval $\left[0, \dfrac{π}{6}\right]$.
$−\dfrac{3}{π}$ | |
$\dfrac{3}{π}$ | |
$\dfrac{9}{π}$ | |
$\dfrac{−9}{π}$ |
Question 12 Explanation:
The correct answer is (C). The integral to be evaluated is:
$\dfrac{1}{\frac{π}{6} − 0} \displaystyle\int_0^{\frac{π}{6}} 3\cos(x)dx$
$\dfrac{6}{π} (3 \sin(x))$
Applying the first fundamental theorem using the bounds given:
$\dfrac{6}{π} \left(3 \sin \left(\dfrac{π}{6}\right) − 3 \sin(0)\right)$
$\dfrac{6}{π} \left(\dfrac{3}{2} − 0\right) = \dfrac{9}{π}$
$\dfrac{1}{\frac{π}{6} − 0} \displaystyle\int_0^{\frac{π}{6}} 3\cos(x)dx$
$\dfrac{6}{π} (3 \sin(x))$
Applying the first fundamental theorem using the bounds given:
$\dfrac{6}{π} \left(3 \sin \left(\dfrac{π}{6}\right) − 3 \sin(0)\right)$
$\dfrac{6}{π} \left(\dfrac{3}{2} − 0\right) = \dfrac{9}{π}$
Question 13 |
$\displaystyle\int \sin^7(x) \cot(x)dx =$
$\dfrac{1}{7}\cos^7(x) + C$ | |
$\dfrac{1}{7}\sin^7(x) + C$ | |
$\dfrac{1}{8}\sin^8(x) + C$ | |
$\dfrac{1}{8}\cos^8(x) + C$ |
Question 13 Explanation:
The correct answer is (B). Since $\cot(x) = \dfrac{\cos(x)}{\sin(x)}$:
$\sin^7(x) \dfrac{\cos(x)}{\sin(x)} = \sin^6(x)\cos(x)$
Thus, the integral to evaluate is:
$\displaystyle\int \sin^6(x) \cos(x)dx$
Using $u = \sin(x)$, $du = \cos(x)dx$
$\displaystyle\int u^6 du$
$\dfrac{1}{7} u^7 + C$
Substituting the value of $u$:
$\dfrac{1}{7} \sin^7(x) + C$
$\sin^7(x) \dfrac{\cos(x)}{\sin(x)} = \sin^6(x)\cos(x)$
Thus, the integral to evaluate is:
$\displaystyle\int \sin^6(x) \cos(x)dx$
Using $u = \sin(x)$, $du = \cos(x)dx$
$\displaystyle\int u^6 du$
$\dfrac{1}{7} u^7 + C$
Substituting the value of $u$:
$\dfrac{1}{7} \sin^7(x) + C$
Question 14 |
$\displaystyle\int_2^3 x^2\sqrt{x^3 − 7}dx =$
$\frac{2}{9}(20)^{\frac{3}{2}} − \frac{2}{9}$ | |
$\frac{2}{9}(1)^{\frac{3}{2}} − \frac{2}{9}$ | |
$\frac{2}{9}(37)^{\frac{3}{2}} − \frac{2}{9}$ | |
$\frac{2}{9}(2)^{\frac{3}{2}} − \frac{2}{9}$ |
Question 14 Explanation:
The correct answer is (A). Let $u = x^3 − 7$, $du = 3x^2dx$, $\frac{1}{3} du = x^2dx$. The integral then becomes:
$\dfrac{1}{3} \displaystyle\int \sqrt{u}$ $du = \dfrac{2}{9} u^{\frac{3}{2}}$
Using $u = x^3 − 7$:
$\dfrac{2}{9} (x^3 − 7)^{\frac{3}{2}}$
Applying the first fundamental theorem using the given bounds:
$\dfrac{2}{9}(20)^{\frac{3}{2}} − \dfrac{2}{9}(1)^{\frac{3}{2}}$
$\dfrac{2}{9}(20)^{\frac{3}{2}} − \dfrac{2}{9}$
$\dfrac{1}{3} \displaystyle\int \sqrt{u}$ $du = \dfrac{2}{9} u^{\frac{3}{2}}$
Using $u = x^3 − 7$:
$\dfrac{2}{9} (x^3 − 7)^{\frac{3}{2}}$
Applying the first fundamental theorem using the given bounds:
$\dfrac{2}{9}(20)^{\frac{3}{2}} − \dfrac{2}{9}(1)^{\frac{3}{2}}$
$\dfrac{2}{9}(20)^{\frac{3}{2}} − \dfrac{2}{9}$
Question 15 |
Identify extrema for the following function.
$f(x) = 3x^3 + \dfrac{45}{2}x^2 + 54x + 3$
$\text{Relative}$ $\text{Maximum}$ $\text{at}$ $x = − 3,$
$\text{Relative}$ $\text{Minimum}$ $\text{at}$ $x = −2$ | |
$\text{Relative}$ $\text{Minimum}$ $\text{at}$ $x = − 3,$
$\text{Relative}$ $\text{Maximum}$ $\text{at}$ $x = −2$ | |
$\text{Absolute}$ $\text{Maximum}$ $\text{at}$ $x = − 3,$
$\text{Absolute}$ $\text{Minimum}$ $\text{at}$ $x = −2$ | |
$\text{Absolute}$ $\text{Minimum}$ $\text{at}$ $x = − 3,$
$\text{Absolute}$ $\text{Maximum}$ $\text{at}$ $x = −2$ |
Question 15 Explanation:
The correct answer is (A). It is known that we can find the extrema of a function by finding its critical points. Therefore, we must find the derivative of the function and set is equal to zero to determine its critical points.
$f'(x) = 9x^2 + 45x + 54 = 0$
$x = −3$, $x = −2$
We can then use a sign pattern to determine the types of extrema that exist at each of the $x$-values.

It is clear from the sign pattern that a relative maximum exists at $x = −3$ and a relative minimum exists at $x = −2$.
Now, to determine if these extrema are absolute extrema, we must identify the end behavior of the function.
$\lim\limits_{x\to −\infty} = − \infty$ $\lim\limits_{x\to \infty} = \infty$
It is clear that the extrema found from the first derivative test are not absolute extrema, as the function ranges over all reals. Therefore, there is a relative maximum at $x = −3$ and a relative minimum at $x = −2$.
$f'(x) = 9x^2 + 45x + 54 = 0$
$x = −3$, $x = −2$
We can then use a sign pattern to determine the types of extrema that exist at each of the $x$-values.

It is clear from the sign pattern that a relative maximum exists at $x = −3$ and a relative minimum exists at $x = −2$.
Now, to determine if these extrema are absolute extrema, we must identify the end behavior of the function.
$\lim\limits_{x\to −\infty} = − \infty$ $\lim\limits_{x\to \infty} = \infty$
It is clear that the extrema found from the first derivative test are not absolute extrema, as the function ranges over all reals. Therefore, there is a relative maximum at $x = −3$ and a relative minimum at $x = −2$.
Question 16 |
Which value of $c$ below satisfies the Mean Value Theorem for the function below on $[3, 5]$?
$f(x) = x^2 − 6x + 15$
$4$ | |
$3$ | |
$0$ | |
$\dfrac{10}{3}$ |
Question 16 Explanation:
The correct answer is (A). It is important to identify that the function given does satisfy the conditions for mean value theorem, as it is continuous and differentiable on the given domain. Therefore, we can identify the slope of the secant line by finding the endpoints.
$f(3) = (3)^2 − 6(3) + 15 = 6$
$f(5) = (5)^2 − 6(5) + 15 = 10$
Therefore, the slope of the secant line is as follows.
$f'(c) = \dfrac{10 − 6}{5 − 3} = \dfrac{4}{2} = 2$
Therefore, we must find a value $x = c$ such that the derivative at $c$ is equal to $2$. Therefore, we must find the derivative of the function and set is equal to $2$ to solve for $c$.
$f'(x) = 2x − 6$
$f'(c) = 2c − 6 = 2$
$c = 4$
$f(3) = (3)^2 − 6(3) + 15 = 6$
$f(5) = (5)^2 − 6(5) + 15 = 10$
Therefore, the slope of the secant line is as follows.
$f'(c) = \dfrac{10 − 6}{5 − 3} = \dfrac{4}{2} = 2$
Therefore, we must find a value $x = c$ such that the derivative at $c$ is equal to $2$. Therefore, we must find the derivative of the function and set is equal to $2$ to solve for $c$.
$f'(x) = 2x − 6$
$f'(c) = 2c − 6 = 2$
$c = 4$
Question 17 |
$\displaystyle\int \dfrac{2x}{\sqrt{16 − x^4}}dx =$
$\arctan \left(\dfrac{x^2}{4}\right) + C$ | |
$\text{arcsec}$ $\left(\dfrac{x^2}{2}\right) + C$ | |
$\arccos \left(\dfrac{x^2}{4}\right) + C$ | |
$\arcsin \left(\dfrac{x^2}{4}\right) + C$ |
Question 17 Explanation:
The correct answer is (D). Let $u = \frac{x^2}{4}$, $dx = \frac{2}{x} du$. Substituting gives
$\displaystyle\int \dfrac{4}{\sqrt{16 − 16u^2}}du$
Simplifying gives the following:
$= \displaystyle\int \dfrac{1}{\sqrt{1 − u^2}}du$
This is in the form of the derivative of $\arcsin(x)$. Thus, the integral is equal to
$\arcsin(u) + C$
Substituting in the value of $u$ gives:
$\arcsin \left(\dfrac{x^2}{4}\right) + C$
$\displaystyle\int \dfrac{4}{\sqrt{16 − 16u^2}}du$
Simplifying gives the following:
$= \displaystyle\int \dfrac{1}{\sqrt{1 − u^2}}du$
This is in the form of the derivative of $\arcsin(x)$. Thus, the integral is equal to
$\arcsin(u) + C$
Substituting in the value of $u$ gives:
$\arcsin \left(\dfrac{x^2}{4}\right) + C$
Question 18 |
Solve the following differential equation given the initial value.
$\dfrac{dy}{dx} = \tan(x), \quad$ $y(0) = 1$
$y = \ln |\cos(x)| + 1$ | |
$y = \ln |\cos(x)|$ | |
$y = −\ln |\cos(x)| + 1$ | |
$y = −\ln |\cos(x)| − 1$ |
Question 18 Explanation:
The correct answer is (C). Start by separating the variables:
$dy = \tan(x) dx$
Integrating both sides to solve for $y$:
$y = −\ln |\cos(x)| + C$
Using the initial value given:
$1 = −\ln |\cos(0)| + C$
$1 = −\ln |1| + C$
$C = 1$
Thus, the answer to the differential equation is:
$y = −\ln |\cos(x)| + 1$
$dy = \tan(x) dx$
Integrating both sides to solve for $y$:
$y = −\ln |\cos(x)| + C$
Using the initial value given:
$1 = −\ln |\cos(0)| + C$
$1 = −\ln |1| + C$
$C = 1$
Thus, the answer to the differential equation is:
$y = −\ln |\cos(x)| + 1$
Question 19 |
If $f(x) = \sqrt{x}$ and $g(x) = x^2 + 3$, identify the following limit.
$\lim\limits_{x\to −4} f(g(x))$
$ \text{DNE}$ | |
$38$ | |
$−1$ | |
$\sqrt{19}$ |
Question 19 Explanation:
The correct answer is (D). We can identify the following limit by first identifying the composite function.
$f(g(x)) = f(x^2 + 3) = \sqrt{x^2 + 3}$
Then, the limit can be identified by substituting the composite function above.
$\lim\limits_{x\to −4} f(g(x))$ $= \lim\limits_{x\to −4} \sqrt{x^2 + 3}$ $= \sqrt{(−4)^2 + 3}$ $= \sqrt{19}$
The limit evaluates to $\sqrt{19}$ by direct substitution.
$f(g(x)) = f(x^2 + 3) = \sqrt{x^2 + 3}$
Then, the limit can be identified by substituting the composite function above.
$\lim\limits_{x\to −4} f(g(x))$ $= \lim\limits_{x\to −4} \sqrt{x^2 + 3}$ $= \sqrt{(−4)^2 + 3}$ $= \sqrt{19}$
The limit evaluates to $\sqrt{19}$ by direct substitution.
Question 20 |
Which of the following properly identifies the tangent line to the curve $f(x) = \sec(2x)$ at $x = \frac{π}{8}$?
$y = 2^{\frac{3}{2}} \cdot x$ | |
$y − \sqrt{2} = \sqrt{2} \left(x − \dfrac{π}{8}\right)$ | |
$y − \sqrt{2} = 2^{\frac{3}{2}} \cdot \left(x − \dfrac{π}{8}\right)$ | |
$y − \dfrac{π}{8} = 2^{\frac{3}{2}} \cdot \left(x − \sqrt{2}\right)$ |
Question 20 Explanation:
The correct answer is (C). We must first identify the slope of the tangent line by identifying the derivative of the function.
$f'(x) = 2 \sec(2x) \tan(2x)$
Then, the slope of the tangent line at $x = \frac{π}{8}$ can be determined by substituting this value into the derivative.
$f' \left(\dfrac{π}{8}\right)$ $= 2\sec \left(\dfrac{2π}{8}\right) \tan \left(\dfrac{2π}{8}\right) $ $= 2\sqrt{2} = 2^{\frac{3}{2}}$
It is important not to forget that the equation for the tangent line in point slope form takes the general form below, where $(x_1, y_1)$ is a given or known point on the function and $m$ is the slope of the line.
$y − y_1 = m(x − x_1)$
Thus, we need a point on the function. However, for the tangent line, we need more than just any point on the function, but actually the specific point on the function that the line is tangent to. We know that the tangent line at $x = \frac{π}{8}$ is tangent to only the point on the function where $x = \frac{π}{8}$. Therefore, we must identify the point on the function where $x = \frac{π}{8}$ to find the known point for the point-slope formula. We can identify the point of tangency by identifying the function value at $x = \frac{π}{8}$.
$f \left(\dfrac{π}{8}\right) = \sec \left(\dfrac{2π}{8}\right)$ $= \dfrac{2}{\sqrt{2}} = \sqrt{2}$
Therefore, the point slope equation for the line tangent to the function at $x = \frac{π}{8}$ is of the form below.
$y − \sqrt{2} = 2^{\frac{3}{2}} \left(x − \dfrac{π}{8}\right)$
$f'(x) = 2 \sec(2x) \tan(2x)$
Then, the slope of the tangent line at $x = \frac{π}{8}$ can be determined by substituting this value into the derivative.
$f' \left(\dfrac{π}{8}\right)$ $= 2\sec \left(\dfrac{2π}{8}\right) \tan \left(\dfrac{2π}{8}\right) $ $= 2\sqrt{2} = 2^{\frac{3}{2}}$
It is important not to forget that the equation for the tangent line in point slope form takes the general form below, where $(x_1, y_1)$ is a given or known point on the function and $m$ is the slope of the line.
$y − y_1 = m(x − x_1)$
Thus, we need a point on the function. However, for the tangent line, we need more than just any point on the function, but actually the specific point on the function that the line is tangent to. We know that the tangent line at $x = \frac{π}{8}$ is tangent to only the point on the function where $x = \frac{π}{8}$. Therefore, we must identify the point on the function where $x = \frac{π}{8}$ to find the known point for the point-slope formula. We can identify the point of tangency by identifying the function value at $x = \frac{π}{8}$.
$f \left(\dfrac{π}{8}\right) = \sec \left(\dfrac{2π}{8}\right)$ $= \dfrac{2}{\sqrt{2}} = \sqrt{2}$
Therefore, the point slope equation for the line tangent to the function at $x = \frac{π}{8}$ is of the form below.
$y − \sqrt{2} = 2^{\frac{3}{2}} \left(x − \dfrac{π}{8}\right)$
Question 21 |
$\displaystyle\int x^2\cos(x^3)dx =$
$\dfrac{1}{3}\sin(x^3) + C$ | |
$\dfrac{1}{3}\sin(x) + C$ | |
$\dfrac{1}{3}\cos(x^3) + C$ | |
$3\sin(x^3) + C$ |
Question 21 Explanation:
The correct answer is (A). Let $u = x^3$, $du = 3x^2 dx$, $\frac{1}{3} du = x^2 dx$
$\dfrac{1}{3} \displaystyle\int \cos(u)du$
$= \dfrac{1}{3} \sin(u) + C$
Substituting in the value of $u$:
$= \dfrac{1}{3}\sin(x^3) + C$
$\dfrac{1}{3} \displaystyle\int \cos(u)du$
$= \dfrac{1}{3} \sin(u) + C$
Substituting in the value of $u$:
$= \dfrac{1}{3}\sin(x^3) + C$
Question 22 |
Which of the following integrals properly identifies the volume of the solid formed by the revolution of the area between the curves $y = x^3$ and $y = x$ around the $x$-axis?
$$π \displaystyle\int_0^1 ((x^3)^2 − (x)^2)dx$$ | |
$$π \displaystyle\int_0^1 (x^3 − x^2)dx$$ | |
$$π \displaystyle\int_0^1 ((x)^2 − (x^3)^2)dx$$ | |
$$2π \displaystyle\int_0^1 ((x^3)^2 − (x)^2)dx$$ |
Question 22 Explanation:
The correct answer is (C). Recall that the formula for finding the area between curves is of the form below, where $f(x)$ is the upper curve and $g(x)$ is the lower curve.
$V = π\displaystyle\int_a^b((f(x))^2 − (g(x))^2 )dx$
It is possible to use intuition to determine which curve is above and which one is below, but we will identify these curves using the graph.
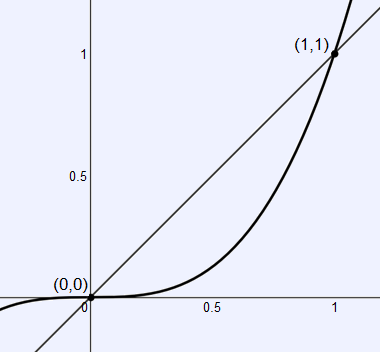
It is clear from the graph that $y = x$ is the upper curve and $y = x^3$ is the lower curve. We can also see from the graph that the functions intersect to form a closed area at $(0, 0)$ and $(1, 1)$. These intersections could also be found algebraically.
Then, by substitution into this formula, we arrive at the integral below.
$V = π \displaystyle\int_0^1 ((x)^2 − (x^3)^2)dx$
$V = π\displaystyle\int_a^b((f(x))^2 − (g(x))^2 )dx$
It is possible to use intuition to determine which curve is above and which one is below, but we will identify these curves using the graph.

It is clear from the graph that $y = x$ is the upper curve and $y = x^3$ is the lower curve. We can also see from the graph that the functions intersect to form a closed area at $(0, 0)$ and $(1, 1)$. These intersections could also be found algebraically.
Then, by substitution into this formula, we arrive at the integral below.
$V = π \displaystyle\int_0^1 ((x)^2 − (x^3)^2)dx$
Question 23 |
$xy = 2x^2 + 3y$.
Solve for $\dfrac{dy}{dx}$
$\dfrac{4x − y + 3}{x}$ | |
$\dfrac{y − 3x}{3}$ | |
$\dfrac{4x − y}{x − 3}$ | |
$\dfrac{x − y}{4x − 3}$ |
Question 23 Explanation:
The correct answer is (C). We shall identify the derivative using implicit differentiation. Be careful about implicit differentiation, as product rule and other rules will apply when they might normally not in traditional differentiation. Be sure to differentiate both sides of the equation.
$x \cdot \dfrac{dy}{dx} + y \cdot \dfrac{dx}{dx}$ $= 4x \cdot \dfrac{dx}{dx} + 3 \cdot \dfrac{dy}{dx}$
We must then isolate for $\dfrac{dy}{dx}$.
$x \cdot \dfrac{dy}{dx} − 3 \cdot \dfrac{dy}{dx}$ $= 4x − y$
$\dfrac{dy}{dx} (x − 3) = 4x − y$
$\dfrac{dy}{dx} = \dfrac{4x − y}{x − 3}$
$x \cdot \dfrac{dy}{dx} + y \cdot \dfrac{dx}{dx}$ $= 4x \cdot \dfrac{dx}{dx} + 3 \cdot \dfrac{dy}{dx}$
We must then isolate for $\dfrac{dy}{dx}$.
$x \cdot \dfrac{dy}{dx} − 3 \cdot \dfrac{dy}{dx}$ $= 4x − y$
$\dfrac{dy}{dx} (x − 3) = 4x − y$
$\dfrac{dy}{dx} = \dfrac{4x − y}{x − 3}$
Question 24 |
Solve for $x$.
$\ln(x^3) − \ln(\sqrt{x}) = 4$
$e^{10}$ | |
$e^{\frac{8}{5}}$ | |
$e^{8}$ | |
$10^{\frac{8}{5}}$ |
Question 24 Explanation:
The correct answer is (B). Recall the log property of subtraction.
$\ln(a) − \ln(b) = \ln \left( \dfrac{a}{b} \right)$
Therefore, we can use this property to simplify.
$\ln(x^3) − \ln(\sqrt{x})$ $= \ln (\frac{x^3}{\sqrt{x}}) $ $= \ln (x^{\frac{5}{2}}) $
Then, recall that there also exists an exponent property for logarithms.
$\ln(a)^b = b \cdot \ln(a)$
Therefore, we can use this property to solve.
$\ln (x^{\frac{5}{2}}) $ $= \dfrac{5}{2} \ln(x)$ $= 4$
$\ln(x) = \dfrac{8}{5}$
$x = e^{\frac{8}{5}}$
$\ln(a) − \ln(b) = \ln \left( \dfrac{a}{b} \right)$
Therefore, we can use this property to simplify.
$\ln(x^3) − \ln(\sqrt{x})$ $= \ln (\frac{x^3}{\sqrt{x}}) $ $= \ln (x^{\frac{5}{2}}) $
Then, recall that there also exists an exponent property for logarithms.
$\ln(a)^b = b \cdot \ln(a)$
Therefore, we can use this property to solve.
$\ln (x^{\frac{5}{2}}) $ $= \dfrac{5}{2} \ln(x)$ $= 4$
$\ln(x) = \dfrac{8}{5}$
$x = e^{\frac{8}{5}}$
Question 25 |
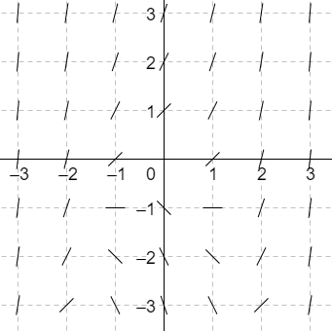 The slope field above is of which of the following differential equations?
The slope field above is of which of the following differential equations?
$\dfrac{dy}{dx} = x + y$ | |
$\dfrac{dy}{dx} = x^2 + y$ | |
$\dfrac{dy}{dx} = x + y^2$ | |
$\dfrac{dy}{dx} = x^2 + y^2$ |
Question 25 Explanation:
The correct answer is (B). Assuming that $x^2 + y$ is the slope of the field, we can test out some points to see if the answer is valid. At $(0, 0)$, the slope will be $0$. At $(0, 1)$, the slope will be $1$. At $(−1, 0)$, the slope will be $1$. Testing out a few more points shows that the slope field given is that of $\frac{dy}{dx} = x^2 + y$.
Question 26 |
Identify the $x$-values where critical points exist for the function below on $0 ≤ x ≤ \sqrt{π}$
$f(x) = \cos(3x^2)$
$0$, $\sqrt{\dfrac{π}{3}}$, $\sqrt{\dfrac{2π}{3}}$, $\sqrt{\dfrac{3π}{3}}$ | |
$\text{No}$ $\text{critical}$ $\text{points}$ $\text{exist}$ $\text{on}$ $\text{the}$ $\text{given}$ $\text{domain}.$ | |
$0, π$ | |
$\sqrt{\dfrac{π}{6}}$, $\sqrt{\dfrac{2π}{6}}$, $\sqrt{\dfrac{3π}{6}}$, $\sqrt{\dfrac{4π}{6}}$ |
Question 26 Explanation:
The correct answer is (A). We must identify the derivative of the function and set it equal to zero to identify the function’s critical points.
$f'(x) = −6x \cdot \sin(3x^2) = 0$
Solving for $x$, we can identify that the solutions are as follows. We shall split solving into two parts.
$−6x = 0$
$x = 0$
$\sin(3x^2) = 0$
$3x^2 = \sin^{−1}(0) = ± πk$
We have written the solution set above in terms of some integer $k$, because we do not want to lose any potential solutions that result from isolating $x$. We will worry about the domain restriction after $x$ has been isolated.
$x^2 = ±$ $\dfrac{πk}{3}$
$x = ±$ $\sqrt{\dfrac{πk}{3}}$
Then, given the domain restrictions, the total solution set is as follows.
$0$, $\sqrt{\dfrac{π}{3}}$, $\sqrt{\dfrac{2π}{3}}$, $\sqrt{\dfrac{3π}{3}}$
$f'(x) = −6x \cdot \sin(3x^2) = 0$
Solving for $x$, we can identify that the solutions are as follows. We shall split solving into two parts.
$−6x = 0$
$x = 0$
$\sin(3x^2) = 0$
$3x^2 = \sin^{−1}(0) = ± πk$
We have written the solution set above in terms of some integer $k$, because we do not want to lose any potential solutions that result from isolating $x$. We will worry about the domain restriction after $x$ has been isolated.
$x^2 = ±$ $\dfrac{πk}{3}$
$x = ±$ $\sqrt{\dfrac{πk}{3}}$
Then, given the domain restrictions, the total solution set is as follows.
$0$, $\sqrt{\dfrac{π}{3}}$, $\sqrt{\dfrac{2π}{3}}$, $\sqrt{\dfrac{3π}{3}}$
Question 27 |
Identify the total distance traveled by a particle that moves according to the function $s(x) = \cos(x)$ from $t = 0$ to $t = π$
$1$ | |
$0$ | |
$\dfrac{1}{2}$ | |
$2$ |
Question 27 Explanation:
The correct answer is (D). Recall that the distance traveled can be found by the integral below.
Distance $= \displaystyle\int_a^b |v(t)|dt$
We must first find the velocity function for the particle.
$s'(x) = v(x) = −\sin(x)$
Then, we can plug this into the formula to find total distance. Notice that the integral must be split into two parts because of the absolute value. The $|−sin(x)|$ is equal to the piece-wise function below.
$|−\sin(x)| =$ $\begin{cases} \sin(x), & 0 ≤ x ≤ \frac{π}{2} \\[2ex] −\sin(x), & \frac{π}{2} < x ≤ π \end{cases}$
$\displaystyle\int_0^π |−sin(x)| dx$ $= \displaystyle\int_0^{\frac{π}{2}} sin(x)dx + \displaystyle\int_{\frac{π}{2}}^π −sin(x)dx$ $= [−\cos(x)]_0^{\frac{π}{2}} + [\cos(x)]_{\frac{π}{2}}^\pi$ $= 2$
Distance $= \displaystyle\int_a^b |v(t)|dt$
We must first find the velocity function for the particle.
$s'(x) = v(x) = −\sin(x)$
Then, we can plug this into the formula to find total distance. Notice that the integral must be split into two parts because of the absolute value. The $|−sin(x)|$ is equal to the piece-wise function below.
$|−\sin(x)| =$ $\begin{cases} \sin(x), & 0 ≤ x ≤ \frac{π}{2} \\[2ex] −\sin(x), & \frac{π}{2} < x ≤ π \end{cases}$
$\displaystyle\int_0^π |−sin(x)| dx$ $= \displaystyle\int_0^{\frac{π}{2}} sin(x)dx + \displaystyle\int_{\frac{π}{2}}^π −sin(x)dx$ $= [−\cos(x)]_0^{\frac{π}{2}} + [\cos(x)]_{\frac{π}{2}}^\pi$ $= 2$
Question 28 |
Which of the following is the value of the derivative of the inverse of the function $f(x) = x^2$ at the mirror point to $(8, 64)$?
$\dfrac{1}{128}$ | |
$64$ | |
$\dfrac{1}{16}$ | |
$\dfrac{1}{2(\sqrt{8})}$ |
Question 28 Explanation:
The correct answer is (C). We shall just use the formula to find the answer. Recall that the formula is as follows, where $g(x)$ is the inverse function of $f(x)$.
$g'(x) = \dfrac{1}{f'(g(x))}$
It was given that $(8, 64)$ was a point on the original function, which has a mirror point of $(64, 8)$ for the inverse function. Thus, the derivative is as follows.
$g'(64) = \dfrac{1}{f'(g(64))}$ $= \dfrac{1}{(f'(8)}$
We can identify the derivative for the function at $x = 8$.
$f'(x) = 2x$
$f'(8) = 16$
Therefore, the derivative of the function’s inverse at $(64, 8)$ is as follows.
$g'(64) = \dfrac{1}{16}$
$g'(x) = \dfrac{1}{f'(g(x))}$
It was given that $(8, 64)$ was a point on the original function, which has a mirror point of $(64, 8)$ for the inverse function. Thus, the derivative is as follows.
$g'(64) = \dfrac{1}{f'(g(64))}$ $= \dfrac{1}{(f'(8)}$
We can identify the derivative for the function at $x = 8$.
$f'(x) = 2x$
$f'(8) = 16$
Therefore, the derivative of the function’s inverse at $(64, 8)$ is as follows.
$g'(64) = \dfrac{1}{16}$
Question 29 |
Which of the following properly identifies the correct acceleration function to the position function below?
$s(t) = \ln(\cos(x^2))$
$a(t) =$ $\dfrac{−2x \cdot \sin(x^2)}{\cos(x^2)}$ | |
$a(t) =$ $−2 \tan(x^2) − 2x \cdot \sec^2(x^2)$ | |
$a(t) =$ $−2 \tan(x^2) − 4x^2 \cdot \sec(x^2) \tan(x^2)$ | |
$a(t) =$ $−2 \tan(x^2) − 4x^2 \cdot \sec^2(x^2)$ |
Question 29 Explanation:
The correct answer is (D). To find the acceleration function, we must take the derivative of the position function twice.
$s'(t) = v(t)$
$= \dfrac{1}{\cos(x^2 )} \cdot −2x \cdot \sin(x^2 )$
$= −2x \cdot \tan(x^2)$
$s''(t) = v'(t) = a(t)$
$= −2x(2x \cdot \sec^2(x^2)) −2\tan(x^2 )$
$= −2 \tan(x^2 ) − 4x^2 sec^2(x^2 )$
$s'(t) = v(t)$
$= \dfrac{1}{\cos(x^2 )} \cdot −2x \cdot \sin(x^2 )$
$= −2x \cdot \tan(x^2)$
$s''(t) = v'(t) = a(t)$
$= −2x(2x \cdot \sec^2(x^2)) −2\tan(x^2 )$
$= −2 \tan(x^2 ) − 4x^2 sec^2(x^2 )$
Question 30 |
$\displaystyle\int \tan^5(x)dx =$
$\frac{1}{4}\sec^4(x) − \frac{1}{2} \sec^2(x) + \ln|\cos(x)| + C$ | |
$\frac{1}{6}\sec^6(x) + C$ | |
$\frac{1}{4}\sec^4(x) − \frac{1}{3} \sec^2(x) + \ln|\cos(x)| + C$ | |
$\frac{1}{4}\sec^4(x) − \sec^2(x) − \ln|\cos(x)| + C$ |
Question 30 Explanation:
The correct answer is (D). Rewrite the integral as follows:
$\displaystyle\int (\tan^2(x))^2 \tan(x)dx$
Since $ \tan^2(x) = \sec^2(x) − 1$:
$\displaystyle\int(\sec^2(x) − 1)^2 \tan(x)dx$
$\displaystyle\int[\sec^4 \text{tan} (x) − 2 \sec^2(x) \tan(x) + \tan(x)]dx$
Separating into three separate integral and evaluating using $u = \sec(x)$ gives
$\dfrac{1}{4}\sec^4(x) − \sec^2(x) − \ln|\cos(x)| + C$
$\displaystyle\int (\tan^2(x))^2 \tan(x)dx$
Since $ \tan^2(x) = \sec^2(x) − 1$:
$\displaystyle\int(\sec^2(x) − 1)^2 \tan(x)dx$
$\displaystyle\int[\sec^4 \text{tan} (x) − 2 \sec^2(x) \tan(x) + \tan(x)]dx$
Separating into three separate integral and evaluating using $u = \sec(x)$ gives
$\dfrac{1}{4}\sec^4(x) − \sec^2(x) − \ln|\cos(x)| + C$
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 30 questions to complete.
|
List |
Next Practice Test:
Multiple Choice Part B >>
AP Calculus Menu >>
