This unit 6 AP Physics C Mechanics practice test reviews a basic understanding of simple harmonic motion and methods of how to solve such systems for various kinematical quantities (like angular frequency) using force and (or) energy considerations in different physical situations. Also, a simple pendulum is dealt with as an example of oscillations.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
A simple pendulum oscillates with an amplitude of $5 \ cm$ and has a phase angle of $10°$. Which of the below options possibly shows the equation of motion for the simple pendulum?
$x(t)=2.5 \ \cos(ωt+10°)$ | |
$x(t)=5 \ \tan(ωt+10°)$ | |
$x(t)=5 \ \sin(ωt)$ | |
$x(t)=2.5 \ \cos(ωt+5°)$ | |
$x(t)=5 \ \sin(ωt+10°)$ |
Question 1 Explanation:
Option A $→$ It is incorrect because, amplitude should be $5 \ cm$ and not $2.5 \ cm$
Option B $→$ It is incorrect because, $\tan \ x$ should be a $\cos \ x$ or $\sin \ x$
Option C $→$ It is incorrect because, phase angle should be $10°$ and not $0°$
Option D $→$ It is incorrect because, amplitude should be $5 \ cm$ and not $2.5 \ cm$
Option E $→$ It is correct because, $x(t)$ is of the form $A \sin (ωt+ϕ)$ where $A$ is the amplitude and $ϕ$ is the phase angle
Option B $→$ It is incorrect because, $\tan \ x$ should be a $\cos \ x$ or $\sin \ x$
Option C $→$ It is incorrect because, phase angle should be $10°$ and not $0°$
Option D $→$ It is incorrect because, amplitude should be $5 \ cm$ and not $2.5 \ cm$
Option E $→$ It is correct because, $x(t)$ is of the form $A \sin (ωt+ϕ)$ where $A$ is the amplitude and $ϕ$ is the phase angle
Question 2 |
A spring-mass system is set into motion by stretching the spring to the right of its equilibrium position and then released.
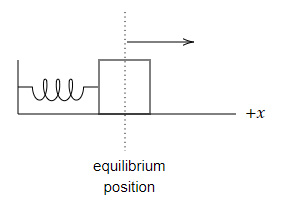
Which of the below graphs shows the correct velocity-time graphs for the system after it is released?
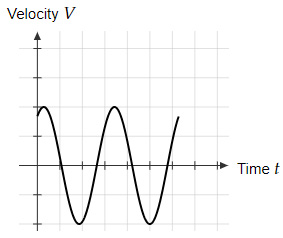 | |
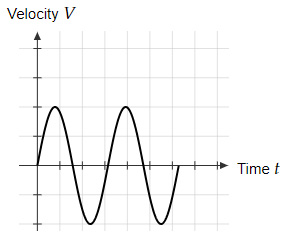 | |
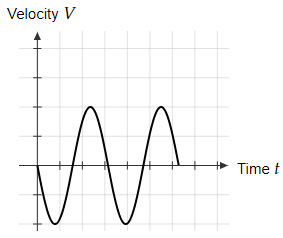 | |
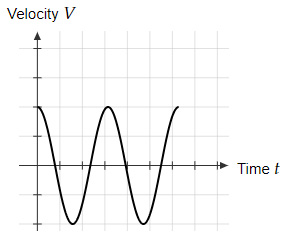 | |
 |
Question 2 Explanation:
After stretching the spring-mass system to the right and then released the position time function should be of the form
$x=A \cos ωt$
And so, the velocity time function should be of the form
$v=-Aω \sin ωt$
Option C represents the function $-Aω \ \sin \ ωt$
$x=A \cos ωt$
And so, the velocity time function should be of the form
$v=-Aω \sin ωt$
Option C represents the function $-Aω \ \sin \ ωt$
Question 3 |
A simple harmonic oscillator moves according to the equation $y(t)=7 \cos\left(\dfrac{πt}{4} + \dfrac{π}{6}\right)$.
When will the oscillator be $2$ units away from the starting position after it starts oscillating from $t=0$?
$0.62$ | |
$0.43$ | |
$0.70$ | |
$0.54$ | |
$0.38$ |
Question 3 Explanation:
Starting position of the oscillator
$=y(t=0)$
$= 7 \cos \left(\dfrac{π}{6}\right)$
$=6.06$
Position of oscillator when it is $2$ units away from the starting position
$=6.06 - 2$
$=4.06$
$7 \ cos \left(\dfrac{πt}{4} + \dfrac{π}{6}\right)=4.06$
Solving for t,
$\dfrac{πt}{4} + \dfrac{π}{6}= \cos^{-1}0.58$
$t=0.54 $
$=y(t=0)$
$= 7 \cos \left(\dfrac{π}{6}\right)$
$=6.06$
Position of oscillator when it is $2$ units away from the starting position
$=6.06 - 2$
$=4.06$
$7 \ cos \left(\dfrac{πt}{4} + \dfrac{π}{6}\right)=4.06$
Solving for t,
$\dfrac{πt}{4} + \dfrac{π}{6}= \cos^{-1}0.58$
$t=0.54 $
Question 4 |
A block of mass $2.5 \ kg$ is attached to a spring of constant $20 \ N/m$. The system is then set into Simple Harmonic Motion by compressing the spring by $4 \ cm$. What is the maximum velocity that the block can have during its motion?
$0.44 \ m/s$ | |
$0.28 \ m/s$ | |
$0.35 \ m/s$ | |
$0.11 \ m/s$ | |
$0.23 \ m/s$ |
Question 4 Explanation:
Potential energy stored in the spring
$=\dfrac{1}{2} kA^2$
$=\dfrac{1}{2}×20×0.04^2$
$=10×0.0016$
$=0.016 \ J $
Maximum kinetic energy of the block
$=\dfrac{1}{2} mv_{max}^2 $
$=0.016 \ J $
Solving for $v_{max}$ gives,
$v_{max}=\sqrt{√2×\dfrac{0.016}{2.5}}=0.11 \ m/s$
$=\dfrac{1}{2} kA^2$
$=\dfrac{1}{2}×20×0.04^2$
$=10×0.0016$
$=0.016 \ J $
Maximum kinetic energy of the block
$=\dfrac{1}{2} mv_{max}^2 $
$=0.016 \ J $
Solving for $v_{max}$ gives,
$v_{max}=\sqrt{√2×\dfrac{0.016}{2.5}}=0.11 \ m/s$
Question 5 |
Look at the position-time graph for a simple pendulum
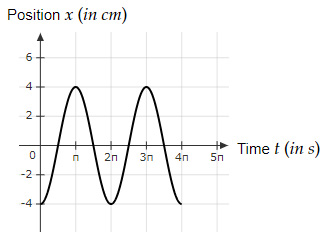
Find the value of time $t$ when the velocity of the simple pendulum reverses its direction for the $1st$ time.
$0 \ sec$ | |
$π/2 \sec $ | |
$π \ sec$ | |
$3π/2 \ sec$ | |
$2π \ sec$ |
Question 5 Explanation:
From time $t=0 \ s$ to $t=π \ s$ the pendulum moved from $x=-4$ to $x=4$
(in the $+x$ direction)
And from time $t=π \ s$ to $t=2π \ s$ the pendulum moved from $x=4$ to $x=-4$
(in the $-x$ direction)
Thus, the velocity of the pendulum changed at time $t=π \ s$
(in the $+x$ direction)
And from time $t=π \ s$ to $t=2π \ s$ the pendulum moved from $x=4$ to $x=-4$
(in the $-x$ direction)
Thus, the velocity of the pendulum changed at time $t=π \ s$
Question 6 |
The equation of motion for a simple harmonic oscillator is given by the relationship,
$x(t)=x_o \sin(ωt+ϕ)$
Derive an expression for the time-dependent acceleration $a(t)$ of the simple harmonic oscillator and thus work out the acceleration at time $t = π/ω$.
$x_o ω^2 \sinϕ$ | |
$x_o ω^2$ | |
$x_o ω^2 \cosϕ$ | |
$x_o ω^2 \sin \dfrac{ϕ}{2}$ | |
$x_o ω^2 \tanϕ$ |
Question 6 Explanation:
$x(t)=x_o \ \sin (ωt+ϕ)$
$v(t)=\dfrac{dx}{dt}=x_o ω \ \cos (ωt+ϕ)$
$a(t)=\dfrac{d^2 x}{dt^2}=-x_o ω^2 \ \sin (ωt+ϕ)$
For $t=\dfrac{π}{ω}$
$a\left(\dfrac{π}{ω}\right)=-x_o ω^2 \sin(ω π/ω+ϕ)$
$=-x_o ω^2 \sin(π+ϕ)$
$=x_o ω^2 \sinϕ $
$v(t)=\dfrac{dx}{dt}=x_o ω \ \cos (ωt+ϕ)$
$a(t)=\dfrac{d^2 x}{dt^2}=-x_o ω^2 \ \sin (ωt+ϕ)$
For $t=\dfrac{π}{ω}$
$a\left(\dfrac{π}{ω}\right)=-x_o ω^2 \sin(ω π/ω+ϕ)$
$=-x_o ω^2 \sin(π+ϕ)$
$=x_o ω^2 \sinϕ $
Question 7 |
Look at the below spring-mass system.
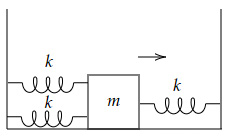
If the spring is displaced slightly to the right, as shown above, then what is the angular frequency $ω$ of the system?
$\sqrt{\dfrac{9k}{m}}$ | |
$\sqrt{\dfrac{3k}{m}}$ | |
$\sqrt{\dfrac{k}{3m}}$ | |
$\sqrt{\dfrac{k}{m}}$ | |
$\sqrt{\dfrac{k}{9m}}$ |
Question 7 Explanation:
Let the displacement of the mass be $x$
Net force acting on the mass $=-3kx$
Thus, $ma=-3kx$
$m \dfrac{d^2 x}{dt^2}=-3kx$
On rearranging, $\dfrac{d^2 x}{dt^2} + \dfrac{3k}{m} x=0$
Thus, $ω^2=\dfrac{3k}{m}→ω=\sqrt{\dfrac{3k}{m}}$
Net force acting on the mass $=-3kx$
Thus, $ma=-3kx$
$m \dfrac{d^2 x}{dt^2}=-3kx$
On rearranging, $\dfrac{d^2 x}{dt^2} + \dfrac{3k}{m} x=0$
Thus, $ω^2=\dfrac{3k}{m}→ω=\sqrt{\dfrac{3k}{m}}$
Question 8 |
The graph represents the potential energy PE of a system as a function of its position $x$.
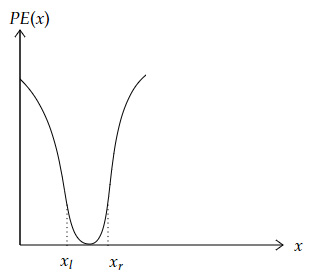
When the system is displaced slightly from its equilibrium position $(x_l ≤ x ≤ x_r)$, it oscillates approximately as a simple harmonic oscillator. Which of the below statements is true regarding the system?
The potential energy of the system is approximately a parabola for $x_l ≤ x ≤ x_r $ | |
The system could perform simple harmonic oscillations for $x ≥ x_r$ | |
The kinetic energy of the system is maximum when it is at $x_r$ or $x_l$ | |
The potential energy of the system has an unstable equilibrium between $x_l$ and $x_r $ | |
The kinetic energy of the system would be independent of the potential energy |
Question 8 Explanation:
Option A $→$ True, as the system performs simple harmonic oscillations for $x∈(x_l,x_r)$
Option B $→$ False, as the potential energy of the system deviates from a parabola for large $x$
Option C $→$ False, as the system is performing simple harmonic motion, the minimum kinetic energy is at its end points ($x_r$ or $x_l$)
Option D $→$ False, the system has a stable equilibrium for $x∈(x_l,x_r)$
Option E $→$ False, the total energy of a simple harmonic oscillator is a constant and so the kinetic energy and potential energy are dependent on each other
Option B $→$ False, as the potential energy of the system deviates from a parabola for large $x$
Option C $→$ False, as the system is performing simple harmonic motion, the minimum kinetic energy is at its end points ($x_r$ or $x_l$)
Option D $→$ False, the system has a stable equilibrium for $x∈(x_l,x_r)$
Option E $→$ False, the total energy of a simple harmonic oscillator is a constant and so the kinetic energy and potential energy are dependent on each other
Question 9 |
The differential equation of a rotating system is given as:
$m \dfrac{d^2 θ}{dt^2} = -j^2 \ θ$
Where m is the mass of the system, $θ$ is the angle of rotation, and $j$ is a positive constant. What is the frequency of the rotating system?
$f=\dfrac{1}{2π} \sqrt{\dfrac{j^2}{m}}$ | |
$=4π \sqrt{\dfrac{j^2}{m}}$ | |
$f=\dfrac{1}{2π} \dfrac{m}{j}$ | |
$f=\dfrac{1}{2π} \dfrac{ \sqrt{m}}{j}$ | |
$f=\dfrac{1}{π} \dfrac{ \sqrt{m}}{j}$ |
Question 9 Explanation:
$m \dfrac{d^2 \ θ}{dt^2}=-j^2 \ θ$
$\dfrac{d^2 \ θ}{dt^2}=-\dfrac{j^2}{m} \ θ$
Or$ \dfrac{d^2 \ θ}{dt^2} + \dfrac{j^2}{m} \ θ=0 $
$\dfrac{d^2 θ}{dt^2}+ω^2 \ θ=0$
Here $ω=\sqrt{\dfrac{j^2}{m}}=2πf$
Thus, $ f=\dfrac{1}{2π} \ \sqrt{ \dfrac{j^2}{m}}$
$\dfrac{d^2 \ θ}{dt^2}=-\dfrac{j^2}{m} \ θ$
Or$ \dfrac{d^2 \ θ}{dt^2} + \dfrac{j^2}{m} \ θ=0 $
$\dfrac{d^2 θ}{dt^2}+ω^2 \ θ=0$
Here $ω=\sqrt{\dfrac{j^2}{m}}=2πf$
Thus, $ f=\dfrac{1}{2π} \ \sqrt{ \dfrac{j^2}{m}}$
Question 10 |
A spring-block system is shown below.
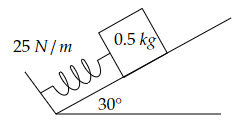
When this system is in equilibrium, the spring is compressed from its natural length. The spring is then compressed by another $4 \ cm$ and then released. What is the velocity of the block when it passes through its equilibrium position?
$0.45 \ m/s$ | |
$0.39 \ m/s$ | |
$0.36 \ m/s$ | |
$0.28 \ m/s$ | |
$0.22 \ m/s$ |
Question 10 Explanation:
Let initial compression be $x_1$ and equilibrium compression be $x_2$
$x_2=\dfrac{mg \ \sinθ}{k}$
$x_2=\dfrac{0.5×10× \sin30°}{25}=0.1 \ m$
Thus, $x_1=0.1+0.04=0.14 \ m$
Initial energy $=\dfrac{1}{2} \ kx_1^2$
$=\dfrac{1}{2}×25×0.14^2 $ $=0.245 \ J$
$h=0.04×\sin30°=0.02 \ m$
Final energy $=mgh+\dfrac{1}{2} \ kx_2^2+\dfrac{1}{2} \ mv^2$
$=0.5×10×0.02+\dfrac{1}{2}×25×0.1^2+\dfrac{1}{2}×0.5×v^2 $ $=0.225+0.25v^2$
Thus, $v^2=\dfrac{0.245-0.225}{0.25=0.08}$
$→v=0.28 \ m/s$
$x_2=\dfrac{mg \ \sinθ}{k}$
$x_2=\dfrac{0.5×10× \sin30°}{25}=0.1 \ m$
Thus, $x_1=0.1+0.04=0.14 \ m$
Initial energy $=\dfrac{1}{2} \ kx_1^2$
$=\dfrac{1}{2}×25×0.14^2 $ $=0.245 \ J$
$h=0.04×\sin30°=0.02 \ m$
Final energy $=mgh+\dfrac{1}{2} \ kx_2^2+\dfrac{1}{2} \ mv^2$
$=0.5×10×0.02+\dfrac{1}{2}×25×0.1^2+\dfrac{1}{2}×0.5×v^2 $ $=0.225+0.25v^2$
Thus, $v^2=\dfrac{0.245-0.225}{0.25=0.08}$
$→v=0.28 \ m/s$
Question 11 |
A simple pendulum satisfies the differential equation $\dfrac{d^2 x}{dt^2} = -\dfrac{g}{l} \ x$. The graph below shows the variation of the time period squared with the length of the pendulum.
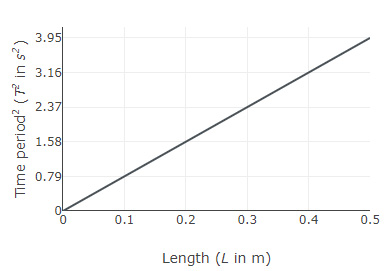
What is the value of $g$ in $m/s^2$?
$4.4 \ m/s^2$ | |
$7.3 \ m/s^2$ | |
$6.5 \ m/s^2$ | |
$9.8 \ m/s^2$ | |
$5.0 \ m/s^2$ |
Question 11 Explanation:
$\dfrac{d^2 x}{dt^2}=-\dfrac{g}{l} x$
$→ω^2=\dfrac{g}{l}$ OR $ω=\sqrt{\dfrac{g}{l}}$
Using $ω=\dfrac{2π}{T}$ and solving for $T^2$ gives,
$T^2=\dfrac{4π^2}{g} \ l$
Slope of the line $=\dfrac{4π^2}{g}=7.9$
$g=\dfrac{4π^2}{7.9}≈5 \ m/s^2$
$→ω^2=\dfrac{g}{l}$ OR $ω=\sqrt{\dfrac{g}{l}}$
Using $ω=\dfrac{2π}{T}$ and solving for $T^2$ gives,
$T^2=\dfrac{4π^2}{g} \ l$
Slope of the line $=\dfrac{4π^2}{g}=7.9$
$g=\dfrac{4π^2}{7.9}≈5 \ m/s^2$
Question 12 |
If $v(t)=-v_o \sin \dfrac{2πt}{T}$ for a simple harmonic oscillator starting from $x(t=0) = \dfrac{v_o \ T}{2π}$ (where v_o>0, and $T$ is the time period of the oscillator), then what is the total distance traveled by the oscillator from time $t=0$ to $t=\dfrac{4T}{3}$?
$3.55 \ \dfrac{v_o \ T}{2π}$ | |
$4.87 \ \dfrac{v_o \ T}{2π}$ | |
$5.50 \ \dfrac{v_o \ T}{2π}$ | |
$4.00 \ \dfrac{v_o \ T}{2π}$ | |
$6.25 \ \dfrac{v_o \ T}{2π}$ |
Question 12 Explanation:
$x=\int v(t) \ dt$
$=\int -v_o \ \sin\dfrac{2πt}{T} dt$
$=C+\dfrac{v_o T}{2π} \ \cos \dfrac{2πt}{T}$
For $t=0, x=\dfrac{v_o \ T}{2π}$
$C+\dfrac{v_o \ T}{2π}= \dfrac{v_o \ T}{2π}→C=0$
$x=\dfrac{v_o T}{2π} \ \cos \dfrac{2πt}{T}$
In one complete period $T$, the distance traveled by the oscillator is $4 \dfrac{v_o \ T}{2π}$
While the distance traveled in time $\dfrac{T}{3}$ is given by,
$|x(T/3)-x(0) |= | \dfrac{v_o \ T}{2π} \ \cos \left( \dfrac{2π}{T} \dfrac{T}{3}\right) - \dfrac{v_o \ T}{2π}|=$
$1.5 \dfrac{v_o \ T}{2π}$
Total distance traveled in time
$\dfrac{4T}{3}=4 \dfrac{v_o \ T}{2π}+1.5 \dfrac{v_o \ T}{2π}=5.5 \dfrac{v_o \ T}{2π}$
$=\int -v_o \ \sin\dfrac{2πt}{T} dt$
$=C+\dfrac{v_o T}{2π} \ \cos \dfrac{2πt}{T}$
For $t=0, x=\dfrac{v_o \ T}{2π}$
$C+\dfrac{v_o \ T}{2π}= \dfrac{v_o \ T}{2π}→C=0$
$x=\dfrac{v_o T}{2π} \ \cos \dfrac{2πt}{T}$
In one complete period $T$, the distance traveled by the oscillator is $4 \dfrac{v_o \ T}{2π}$
While the distance traveled in time $\dfrac{T}{3}$ is given by,
$|x(T/3)-x(0) |= | \dfrac{v_o \ T}{2π} \ \cos \left( \dfrac{2π}{T} \dfrac{T}{3}\right) - \dfrac{v_o \ T}{2π}|=$
$1.5 \dfrac{v_o \ T}{2π}$
Total distance traveled in time
$\dfrac{4T}{3}=4 \dfrac{v_o \ T}{2π}+1.5 \dfrac{v_o \ T}{2π}=5.5 \dfrac{v_o \ T}{2π}$
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 12 questions to complete.
|
List |
Next Practice Test:
Unit 7: Gravitation >>
AP Physics C Mechanics Main Menu >>
