Our AP Physics C Mechanics unit 7 practice test covers gravitation. To answer these questions you should be familiar with Newton’s laws of Gravitation and their applications to different systems. Also, the motion of satellites, variation of gravitational acceleration with height, gravitational potential energy, and Kepler’s laws are included topics.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
Find the force of gravity between two-point particles of mass $2.5 \ kg$ and $3.0 \ kg$ which are at a distance of $10 \ cm$ from each other.
$50.03×10^{-9} \ N$ | |
$50.03×10^{-11} \ N$ | |
$0.50×10^{-8} \ N$ | |
$5.03×10^{-9} \ N$ | |
$0.05×10^{-10} \ N$ |
Question 1 Explanation:
$F_g=\dfrac{Gm_1 m_2}{r^2}$
Using $G=6.67×10^{-11}, \ m_1=2.5 \ kg,m_2=3.0 \ kg$ and $r=0.1 \ m$ in the above equation gives,
$F_g=\dfrac{6.67×10^{-11}×2.5×3}{0.1^2} = 50.03×10^{-9} \ N$
Using $G=6.67×10^{-11}, \ m_1=2.5 \ kg,m_2=3.0 \ kg$ and $r=0.1 \ m$ in the above equation gives,
$F_g=\dfrac{6.67×10^{-11}×2.5×3}{0.1^2} = 50.03×10^{-9} \ N$
Question 2 |
Three stars in the Milky Way were found in the following symmetrical arrangement.
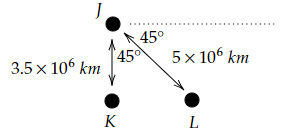
What is the net force acting on star J due to the other two stars?
(The mass of each star is equal to $6 × 10^{28} \ kg$ and the $XY$ axis is in standard orientation)
$(9.68 \skew{2.3}\hat{i} - 29.20 \skew{4.5}\hat{j} )×10^{24} \ N$ | |
$(9.60 \skew{2.3}\hat{i} + 29.25 \skew{4.5}\hat{j} )×10^{25} \ N$ | |
$(29.20\skew{2.3}\hat{i} + 9.60 \skew{4.5}\hat{j} )×10^{27} \ N$ | |
$(6.78 \skew{2.3}\hat{i} - 26.38 \skew{4.5}\hat{j} )×10^{27} \ N$ | |
$(19.45 \skew{2.3}\hat{i} - 9.20 \skew{4.5}\hat{j} )×10^{26} \ N$ |
Question 2 Explanation:
Force on $J$ due to $K =\dfrac{Gm^2}{r^2}$
$=\dfrac{6.67×10^{-11}×36×10^{56}}{12.25×10^{18} }$
$=19.6×10^{27} \ N$ (along $-\skew{5}\hat{j}$)
Force on $J$ due to $L=\dfrac{Gm^2}{r^2}$
$=\dfrac{6.67×10^{-11}×36×10^{56}}{25×10^{18}}$
$=9.60×10^{27} \ N$ (along $\left(\dfrac{\skew{2}\hat{i}}{\sqrt{2}}-\dfrac{\skew{5}\hat{j}}{\sqrt{2}}\right)$)
Net force $=(6.78\skew{2}\hat{i}-26.38\skew{5}\hat{j} )×10^{27} \ N$
$=\dfrac{6.67×10^{-11}×36×10^{56}}{12.25×10^{18} }$
$=19.6×10^{27} \ N$ (along $-\skew{5}\hat{j}$)
Force on $J$ due to $L=\dfrac{Gm^2}{r^2}$
$=\dfrac{6.67×10^{-11}×36×10^{56}}{25×10^{18}}$
$=9.60×10^{27} \ N$ (along $\left(\dfrac{\skew{2}\hat{i}}{\sqrt{2}}-\dfrac{\skew{5}\hat{j}}{\sqrt{2}}\right)$)
Net force $=(6.78\skew{2}\hat{i}-26.38\skew{5}\hat{j} )×10^{27} \ N$
Question 3 |
A satellite is moving in a circular orbit at a fixed distance of $1,000 \ km$ from the surface of the Earth. What is the time period of this satellite?
$(M_e=6×10^{24} \ kg, \ R_e=6400 \ km)$
$2.05 \ hr$ | |
$1.52 \ hr$ | |
$1.75 \ hr$ | |
$1.88 \ hr$ | |
$2.15 \ hr$ |
Question 3 Explanation:
For a satellite moving in a circular orbit,
$\dfrac{m_s v^2}{r} = \dfrac{GM_e m_s}{r^2}$
$v_s=\sqrt{\dfrac{GM_e}{r}}$
Here $r=R_e+1,000 \ km$
Using $r=7.4×10^6 m$ and $M_e=6×10^{24} \ kg$
$v_s=\sqrt{\dfrac{6.67×10^{-11}×6×10^{24}}{7.4×10^6 }}=7,348 \ m/s$
Using $ T=\dfrac{2πr}{v_s}$ gives $T=6327.6 \ s=1.75 hr $
$\dfrac{m_s v^2}{r} = \dfrac{GM_e m_s}{r^2}$
$v_s=\sqrt{\dfrac{GM_e}{r}}$
Here $r=R_e+1,000 \ km$
Using $r=7.4×10^6 m$ and $M_e=6×10^{24} \ kg$
$v_s=\sqrt{\dfrac{6.67×10^{-11}×6×10^{24}}{7.4×10^6 }}=7,348 \ m/s$
Using $ T=\dfrac{2πr}{v_s}$ gives $T=6327.6 \ s=1.75 hr $
Question 4 |
Alex drops one object from points A and B each. He then finds the ratio of acceleration due to gravity for those objects.
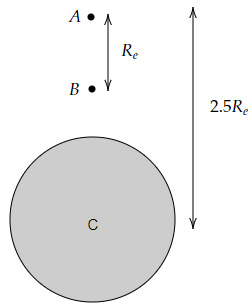
Which of the below options shows the ratio obtained by Alex?
$0.54 ∶ 1$ | |
$0.49 ∶ 1$ | |
$0.45 ∶ 1$ | |
$0.60 ∶ 1$ | |
$0.36 ∶ 1$ |
Question 4 Explanation:
If $h$= Distance from the surface of the Earth then,
$g(h)=\dfrac{GM_e}{(R_e+h)^2}$
For point $A, h=2.5R_e-R_e=1.5R_e$
$g(h)=\dfrac{GM_e}{(R_e+1.5R_e )^2} =\dfrac{GM_e}{6.25R_e^2}$
For point $B, h=1.5R_e-R_e=0.5R_e$
$g(h)=\dfrac{GM_e}{(R_e+0.5R_e )^2} =\dfrac{GM_e}{2.25R_e^2}$
Ratio of acceleration $=\dfrac{GM_e}{6.25R_e^2 }×\dfrac{2.25R_e^2}{GM_e}=0.36 ∶ 1$
$g(h)=\dfrac{GM_e}{(R_e+h)^2}$
For point $A, h=2.5R_e-R_e=1.5R_e$
$g(h)=\dfrac{GM_e}{(R_e+1.5R_e )^2} =\dfrac{GM_e}{6.25R_e^2}$
For point $B, h=1.5R_e-R_e=0.5R_e$
$g(h)=\dfrac{GM_e}{(R_e+0.5R_e )^2} =\dfrac{GM_e}{2.25R_e^2}$
Ratio of acceleration $=\dfrac{GM_e}{6.25R_e^2 }×\dfrac{2.25R_e^2}{GM_e}=0.36 ∶ 1$
Question 5 |
A satellite is launched from the surface of a planet such that it escapes the gravitational field and travels with a speed of $10 \ km/s$ thereafter. Determine the velocity with which the satellite must be launched. (Take the mass of the planet as $3×10^{26} \ kg$ and the radius as $8×10^7 \ m$.)
$22.8 \ km/s$ | |
$24.4 \ km/s$ | |
$26.9 \ km/s$ | |
$29.5 \ km/s$ | |
$21.6 \ km/s$ |
Question 5 Explanation:
Total energy of the satellite far away from the planet $=\dfrac{1}{2} mv_{away}^2$
Total energy of the satellite on the surface of the planet $=\dfrac{1}{2} mv_{esc}^2 - \dfrac{GM_p m}{R_p}$
Equating the two equations gives,
$\dfrac{1}{2} mv_{away}^2=\dfrac{1}{2} mv_{esc}^2 - \dfrac{GM_p m}{R_p}$
$v_{away}^2=v_{esc}^2-\dfrac{2GM_p}{R_p}$
Using $v_{away}=10^4 \ m/s, M_p=3×10^{26} \ kg$ and $R_p=8×10^7 m$ gives,
$v_{esc}^2=v_{away}^2+\dfrac{2GM_p}{R_p}$
$v_{esc}^2=(10^4 )^2+\dfrac{2×6.67×10^{-11}×3×10^{26}}{8×10^7}$
$v_{esc}^2=10^8+5.00×10^8$
$v_{esc}^2=6.00×10^8$
$v_{esc}=2.44×10^4 \ m/s$
$v_{esc}=24.4 \ km/s$
Total energy of the satellite on the surface of the planet $=\dfrac{1}{2} mv_{esc}^2 - \dfrac{GM_p m}{R_p}$
Equating the two equations gives,
$\dfrac{1}{2} mv_{away}^2=\dfrac{1}{2} mv_{esc}^2 - \dfrac{GM_p m}{R_p}$
$v_{away}^2=v_{esc}^2-\dfrac{2GM_p}{R_p}$
Using $v_{away}=10^4 \ m/s, M_p=3×10^{26} \ kg$ and $R_p=8×10^7 m$ gives,
$v_{esc}^2=v_{away}^2+\dfrac{2GM_p}{R_p}$
$v_{esc}^2=(10^4 )^2+\dfrac{2×6.67×10^{-11}×3×10^{26}}{8×10^7}$
$v_{esc}^2=10^8+5.00×10^8$
$v_{esc}^2=6.00×10^8$
$v_{esc}=2.44×10^4 \ m/s$
$v_{esc}=24.4 \ km/s$
Question 6 |
The figure below shows the motion of a planet around the Sun.
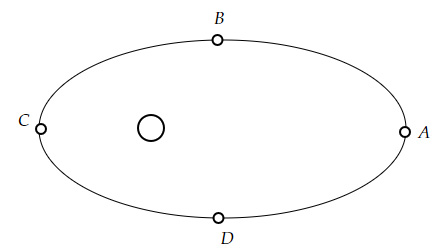
In which position does the planet travel with the fastest speed around the Sun?
$D$ | |
$C$ | |
$B$ | |
$A$ | |
None of the above |
Question 6 Explanation:
Since, the Sun-Planet system is isolated the total mechanical energy is conserved
And total energy at any point on the trajectory is given by the expression,
$TE=\dfrac{1}{2} mv^2 - \dfrac{GMm}{r} $
For the speed (or kinetic energy) to be maximum, the term $\dfrac{GMm}{r}$ should be as large as possible (so that the difference remains a constant)
$\dfrac{GMm}{r}$ is maximum when $r$ is small
Thus, the planet has the highest speed at point $C$
And total energy at any point on the trajectory is given by the expression,
$TE=\dfrac{1}{2} mv^2 - \dfrac{GMm}{r} $
For the speed (or kinetic energy) to be maximum, the term $\dfrac{GMm}{r}$ should be as large as possible (so that the difference remains a constant)
$\dfrac{GMm}{r}$ is maximum when $r$ is small
Thus, the planet has the highest speed at point $C$
Question 7 |
What is the total mechanical energy of a satellite that is orbiting a planet at a distance of $1.5 × 10^{10} \ m$ from the center of the planet?
(Assume the mass of the planet to be 5×10^25 kg and the mass of the satellite to be 1.2 × 10^2 \kg)
$-16.24 × 10^6 \ J$ | |
$-10.17 × 10^6 \ J$ | |
$-11.02 × 10^6 \ J$ | |
$-15.82 × 10^6 \ J$ | |
$-13.34 × 10^6 \ J$ |
Question 7 Explanation:
For a satellite moving about a planet in a circular orbit,
$v=\sqrt{\dfrac{GM_p}{r}}→KE=\dfrac{1}{2} \dfrac{ GM_p m_s}{r} $
$PE=-\dfrac{GM_p m_s}{r}$
$TE=PE+KE$
$TE=-\dfrac{1}{2} \dfrac{GM_p m_s}{r} $
Using $M_p=5×10^{25} \ kg, r=1.5×10^{10} \ m, m_s=1.2×10^2 \ kg$
$TE=-\dfrac{1}{2} \dfrac{6.67×10^{-11}×5×10^{25}×1.2×10^2}{1.5×10^{10}}$
$TE=-13.34×10^6 \ J $
$v=\sqrt{\dfrac{GM_p}{r}}→KE=\dfrac{1}{2} \dfrac{ GM_p m_s}{r} $
$PE=-\dfrac{GM_p m_s}{r}$
$TE=PE+KE$
$TE=-\dfrac{1}{2} \dfrac{GM_p m_s}{r} $
Using $M_p=5×10^{25} \ kg, r=1.5×10^{10} \ m, m_s=1.2×10^2 \ kg$
$TE=-\dfrac{1}{2} \dfrac{6.67×10^{-11}×5×10^{25}×1.2×10^2}{1.5×10^{10}}$
$TE=-13.34×10^6 \ J $
Question 8 |
The time period of two satellites, $LI$ and $MBII$, moving around the Earth is $24 \ hours$ and $2.5 \ hours$, respectively. The distance of the satellite $LI$ is approximately $36,000 \ km$ from the center of the Earth. What is the distance between $MBII$ satellite from the center of the Earth?
$6,324 \ km$ | |
$7,204 \ km$ | |
$8,122 \ km$ | |
$7,964 \ km$ | |
$7,684 \ km$ |
Question 8 Explanation:
According to Kepler’s 3rd law,
$T^2∝r^3$
Thus,
$\left(\dfrac{T_{MBII}}{T_{LI}} \right)^2=\left( \dfrac{r_{MBII}}{r_{LI}} \right)^3$
$\left(\dfrac{2.5}{24}\right)^2= \left(\dfrac{r_{MBII}}{36,000}\right)^3$
$\left( \dfrac{r_{MBII}}{36,000}\right)^3=\dfrac{1}{92.16}$
Solving for $r_{MBII}$ gives,
$r_{MBII}=\dfrac{36,000}{4.52}=7,964 \ km$
$T^2∝r^3$
Thus,
$\left(\dfrac{T_{MBII}}{T_{LI}} \right)^2=\left( \dfrac{r_{MBII}}{r_{LI}} \right)^3$
$\left(\dfrac{2.5}{24}\right)^2= \left(\dfrac{r_{MBII}}{36,000}\right)^3$
$\left( \dfrac{r_{MBII}}{36,000}\right)^3=\dfrac{1}{92.16}$
Solving for $r_{MBII}$ gives,
$r_{MBII}=\dfrac{36,000}{4.52}=7,964 \ km$
Question 9 |
The acceleration due to gravity varies at large distances from the surface of the Earth. If an object is dropped at a distance of $h$ from the surface of the Earth, then what is the velocity of the object $v$ as a function of its displacement $x$?
(Hint: You might find the relation $ \dfrac{dv}{dt} = v \dfrac{dv}{dx}$ helpful)
$v(x)=2 \sqrt{ \dfrac{GM}{R_e+h-x} - \dfrac{GM}{R_e+h}}$ | |
$v(x)=2 \sqrt{ \dfrac{GM}{R_e+h+x}}$ | |
$v(x)=2 \sqrt{ \dfrac{GM}{R_e+h-x}}$ | |
$v(x)=2 \sqrt{ \dfrac{GM}{R_e+h} - \dfrac{GM}{R_e+h+x}}$ | |
$v(x)=2 \sqrt{ \dfrac{GM}{R_e+h} + \dfrac{GM}{R_e+h+x}}$ |
Question 9 Explanation:
$\dfrac{dv}{dt} = \dfrac{GM}{r^2}$
Using the differential equation from the question gives,
$v \dfrac{dv}{dx} = \dfrac{GM}{r^2}$
Note: $r=R_e+(h-x)$
Solving the differential equation gives,
$\dfrac{v^2}{2}=C + \dfrac{GM}{R_e+h-x}$
At $x=0, \ v=0$ which implies $C= - \dfrac{GM}{R_e+h}$
$v(x)=2 \sqrt{ \dfrac{GM}{R_e+h-x} - \dfrac{GM}{R_e+h}}$
Using the differential equation from the question gives,
$v \dfrac{dv}{dx} = \dfrac{GM}{r^2}$
Note: $r=R_e+(h-x)$
Solving the differential equation gives,
$\dfrac{v^2}{2}=C + \dfrac{GM}{R_e+h-x}$
At $x=0, \ v=0$ which implies $C= - \dfrac{GM}{R_e+h}$
$v(x)=2 \sqrt{ \dfrac{GM}{R_e+h-x} - \dfrac{GM}{R_e+h}}$
Question 10 |
Two planets are aligned in such a way that they always face each other while moving in their respective orbits. A small rover is to be launched from planet $A$ to planet $B$.
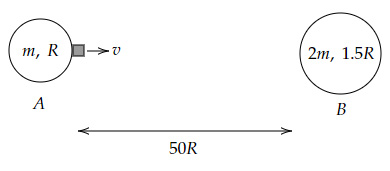
What should be the speed v of the rover with which it should be launched from planet $A$ so that it reaches planet $B$ with a speed of $u = \sqrt{ \dfrac{4Gm}{R}}$?
(Note: The values inside the circles shows the mass and the radius of the planet respectively.)
$\sqrt{\dfrac{1.66Gm}{R}}$ | |
$\sqrt{\dfrac{2.41Gm}{R}}$ | |
$\sqrt{\dfrac{3.38Gm}{R}}$ | |
$\sqrt{\dfrac{2.02Gm}{R}}$ | |
$\sqrt{\dfrac{4.56Gm}{R}}$ |
Question 10 Explanation:
Total energy of rover on planet
$A=\dfrac{1}{2} m_r v^2 - \dfrac{Gmm_r}{R} - \dfrac{2Gmm_r}{51.5R}$
$=\dfrac{1}{2} m_r v^2-1.04 \dfrac{Gmm_r}{R}$
Total energy of rover on planet
$B=\dfrac{1}{2} m_r \left(\dfrac{4Gm}{R}\right)-\dfrac{Gmm_r}{51R} - \dfrac{2Gmm_r}{1.5R}$
$=2 \dfrac{Gmm_r}{R-1.35} \dfrac{Gmm_r}{R}$
$=0.65 \dfrac{Gmm_r}{R}$
Since the total mechanical energy of the rover is a constant
$\dfrac{1}{2} m_r v^2-1.04 \dfrac{Gmm_r}{R}=0.65 \dfrac{Gmm_r}{R}$
$\dfrac{1}{2} m_r v^2=1.69 \dfrac{Gmm_r}{R}$
$v^2=\dfrac{3.38Gm}{R}$
$v=\sqrt{ \dfrac{3.38Gm}{R}} $
$A=\dfrac{1}{2} m_r v^2 - \dfrac{Gmm_r}{R} - \dfrac{2Gmm_r}{51.5R}$
$=\dfrac{1}{2} m_r v^2-1.04 \dfrac{Gmm_r}{R}$
Total energy of rover on planet
$B=\dfrac{1}{2} m_r \left(\dfrac{4Gm}{R}\right)-\dfrac{Gmm_r}{51R} - \dfrac{2Gmm_r}{1.5R}$
$=2 \dfrac{Gmm_r}{R-1.35} \dfrac{Gmm_r}{R}$
$=0.65 \dfrac{Gmm_r}{R}$
Since the total mechanical energy of the rover is a constant
$\dfrac{1}{2} m_r v^2-1.04 \dfrac{Gmm_r}{R}=0.65 \dfrac{Gmm_r}{R}$
$\dfrac{1}{2} m_r v^2=1.69 \dfrac{Gmm_r}{R}$
$v^2=\dfrac{3.38Gm}{R}$
$v=\sqrt{ \dfrac{3.38Gm}{R}} $
Question 11 |
Which of the below statements is TRUE regarding Kepler’s 2nd law?
The area swept per unit time by a planet changes at every point on the orbit | |
The time taken to complete an orbit is proportional to the $1.5th$ power of the radius of the orbit | |
Kepler’s 2nd law is a consequence of the conservation of angular momentum in central forces | |
The angular momentum of the planet changes at every point on the orbit | |
Kepler’s 2nd law is true only for circular orbits |
Question 11 Explanation:
Option A $→$ False, because the area swept per unit time is a constant
Option B $→$ False, because the 2nd law of Kepler is based on rate of change of area
Option C $→$ True, because the 2nd law of Kepler can be derived using law of conservation of angular momentum
Option D $→$ False, because the angular momentum of the planet is a constant
Option E $→$ False, because it is true for circular and elliptical orbits
Option B $→$ False, because the 2nd law of Kepler is based on rate of change of area
Option C $→$ True, because the 2nd law of Kepler can be derived using law of conservation of angular momentum
Option D $→$ False, because the angular momentum of the planet is a constant
Option E $→$ False, because it is true for circular and elliptical orbits
Question 12 |
Look at the figure below.
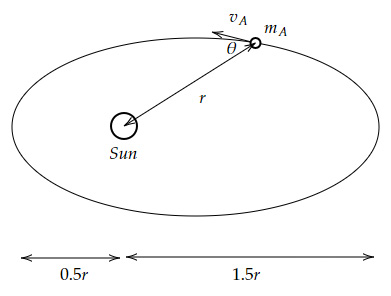
What should be the perihelion speed of planet $A$?
$1.5v_A \ \cos θ$ | |
$0.5v_A \ \sin θ$ | |
$2v_A \ \cos θ$ | |
$2v_A \ \sin θ$ | |
$3.5v_A \ \tan θ$ |
Question 12 Explanation:
At point shown,
Angular momentum
$L=m_A v_A r \ \sin (π-θ)$
$=m_A v_A r \ \sin θ$
Perihelion speed is when the planet is closest to the Sun
At perihelion,
Angular momentum
$L=m_A v_A' \ (0.5r) \ \sin 90° $
$=0.5m_A v_A' r $
Thus, $v_A'=2v_A \ \sin θ$
Angular momentum
$L=m_A v_A r \ \sin (π-θ)$
$=m_A v_A r \ \sin θ$
Perihelion speed is when the planet is closest to the Sun
At perihelion,
Angular momentum
$L=m_A v_A' \ (0.5r) \ \sin 90° $
$=0.5m_A v_A' r $
Thus, $v_A'=2v_A \ \sin θ$
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 12 questions to complete.
|
List |
More Practice Tests:
AP Physics C Mechanics Main Menu >>
