This free AP Physics C unit 5 practice test on rotation consists of rotational analogs of linear quantities like angular displacement, angular velocity, and similar kinematical relations. Also, concepts of moment of inertia for discrete and continuous systems, rotational stability, and the law of conservation of angular momentum are considered.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
A small disk is rotating about an axis perpendicular to the plane of the disc and passing through its center $C$. The disk changed its angular speed from $7 \ rad/s$ to $12 \ rad/s$ in $3 \ s$. What is the angular displacement of the disk in this time period?
$24.3 \ rad$ | |
$30.2 \ rad$ | |
$28.5 \ rad$ | |
$20.7 \ rad$ | |
$19.2 \ rad$ |
Question 1 Explanation:
Angular acceleration $α=\dfrac{12-7}{3}=1.67 \ rad/s^2$
Using $α=1.67 \ rad/s^2, ω_o=7 \ rad/s, \ t=3 s$ in the equation $Δθ=ω_o t+\dfrac{1}{2} αt^2$
$ Δθ=7×3+\dfrac{1}{2}×1.67×3^2=28.5 \ rad$
Using $α=1.67 \ rad/s^2, ω_o=7 \ rad/s, \ t=3 s$ in the equation $Δθ=ω_o t+\dfrac{1}{2} αt^2$
$ Δθ=7×3+\dfrac{1}{2}×1.67×3^2=28.5 \ rad$
Question 2 |
The below rod is in mechanical equilibrium.

$C$ represents the center of the rod, and it has a length of $20 \ cm$. Find the magnitude $F$ and the direction $θ$ for the force applied on the right edge.
$F=25 \ N$ and $θ=53.1°$ | |
$F=20 \ N$ and $θ=40.2°$ | |
$F=30 \ N$ and $θ=30.6°$ | |
$F=34 \ N$ and $θ=53.1°$ | |
$F=25 \ N$ and $θ=60.0$° |
Question 2 Explanation:
Resolve the force acting on the right edge as follows:
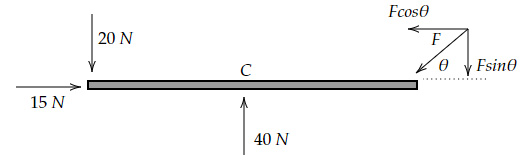
For translational equilibrium,
$F \cos θ=15$ and $20+F \sin θ=40$
For rotational equilibrium,
$-20×10+F \sinθ×10=0$
$→ F \sin θ=20 \ N$ and $F \cos θ=15 \ N$
$F=\sqrt{20^2+15^2}=25 \ N$
And, $\tan θ=\dfrac{20}{15}=1.33$
Or $θ≈53.1°$

For translational equilibrium,
$F \cos θ=15$ and $20+F \sin θ=40$
For rotational equilibrium,
$-20×10+F \sinθ×10=0$
$→ F \sin θ=20 \ N$ and $F \cos θ=15 \ N$
$F=\sqrt{20^2+15^2}=25 \ N$
And, $\tan θ=\dfrac{20}{15}=1.33$
Or $θ≈53.1°$
Question 3 |
Two hard spheres of mass $2 \ kg$ each are $1 \ m$ apart. When the distance between the two spheres is increased to $1.5 \ m$, the moment of inertia of the system of two spheres increases to,
(The axis of rotation passes through the midpoint of the line joining the two spheres)
$2.50 \ kgm^2$ | |
$3.00 \ kgm^2$ | |
$4.00 \ kgm^2$ | |
$3.50 \ kgm^2$ | |
$2.25 \ kgm^2$ |
Question 3 Explanation:
Distance of each sphere from the midpoint of the line joining the two spheres
$=\dfrac{1.5}{2}$
$=0.75 \ m$
Moment of inertia
$=∑mr^2$
$=2×0.75^2+2×0.75^2$
$=2.25 \ kgm^2$
$=\dfrac{1.5}{2}$
$=0.75 \ m$
Moment of inertia
$=∑mr^2$
$=2×0.75^2+2×0.75^2$
$=2.25 \ kgm^2$
Question 4 |
The angular displacement of a body is given by the formula,
$θ(t)=2t(1+t^3 )$
where $θ$ is in $rad$ and $t$ is in $s$. Which graph best represents the angular acceleration of the body?
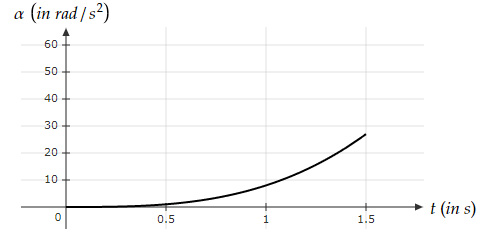 | |
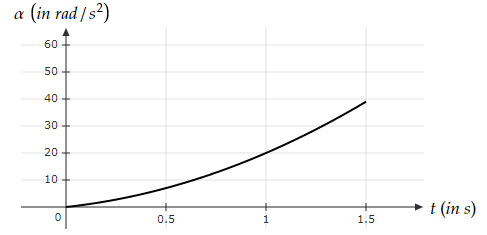 | |
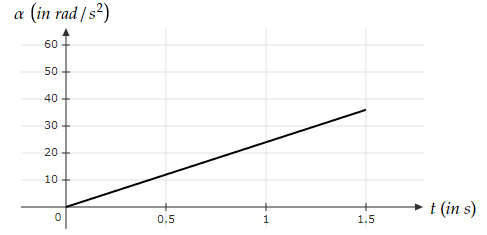 | |
 | |
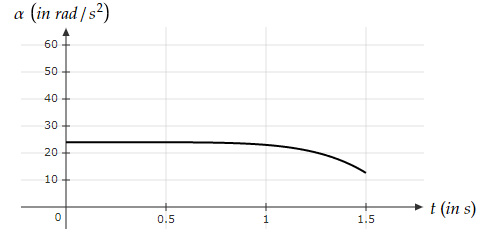 |
Question 4 Explanation:
$θ(t)=2t(1+t^3 )=2t+2t^4 $
$ω=\dfrac{d}{dt} θ(t)=2+8t^3 $
$α=\dfrac{d}{dt} ω(t)=24t^2 $
Option D has all these values approximately true
$ω=\dfrac{d}{dt} θ(t)=2+8t^3 $
$α=\dfrac{d}{dt} ω(t)=24t^2 $
| $α$ | $0$ | $6$ | $24$ | $54$ |
| $t$ | $0$ | $0.5$ | $1$ | $1.5$ |
Question 5 |
A wheel of radius $4 \ cm$ is rolling on a surface without slipping with an angular velocity of $2 \ rad/s$, as shown in the figure below.
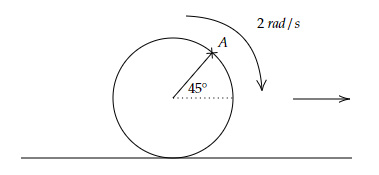
It is known that the net velocity of point A is the vector sum of the velocity of the center of mass and the (rotational) velocity of point A about the center of mass. What is the magnitude of the net velocity of point $A$?
(Hint: Velocity of Center of Mass for motion without slipping is $ω × r$)
$13.5 \ cm/s$ | |
$14.8 \ cm/s$ | |
$18.0 \ cm/s$ | |
$12.5 \ cm/s$ | |
$15.7 \ cm/s$ |
Question 5 Explanation:
Velocity of any point on the wheel is equal to the vector sum of the translational and rotational velocity
Velocity of the center of mass $=ω×r=8 \ cm/s$ (along $\skew{2}\hat{i}$)
For point A, Rotational velocity $=ω×r=8 \ cm/s$
And its direction is along the tangent to the circle at point A,
That is along $(\cos45° \skew{2}\hat{i} - \sin 45° \skew{5}\hat{j})=\dfrac{1}{\sqrt{2}} (\skew{2}\hat{i} - \skew{5}\hat{j})$
Net velocity $=\left(8\skew{2}\hat{i} + \dfrac{8}{\sqrt{2}} (\skew{2}\hat{i} - \skew{5}\hat{j} )\right)=(8+4\sqrt{2}) \skew{2}\hat{i} -4\sqrt{2} \skew{5}\hat{j} \ cm/s$
Magnitude of linear velocity $=\sqrt{13.65^2+5.65^2 } = 14.77 \ cm/s $
Velocity of the center of mass $=ω×r=8 \ cm/s$ (along $\skew{2}\hat{i}$)
For point A, Rotational velocity $=ω×r=8 \ cm/s$
And its direction is along the tangent to the circle at point A,
That is along $(\cos45° \skew{2}\hat{i} - \sin 45° \skew{5}\hat{j})=\dfrac{1}{\sqrt{2}} (\skew{2}\hat{i} - \skew{5}\hat{j})$
Net velocity $=\left(8\skew{2}\hat{i} + \dfrac{8}{\sqrt{2}} (\skew{2}\hat{i} - \skew{5}\hat{j} )\right)=(8+4\sqrt{2}) \skew{2}\hat{i} -4\sqrt{2} \skew{5}\hat{j} \ cm/s$
Magnitude of linear velocity $=\sqrt{13.65^2+5.65^2 } = 14.77 \ cm/s $
Question 6 |
A body of moment of inertia $I$ undergoes rotational motion (starting from rest) due to constant torque $τ$ acting on it. If the angular displacement of the body is equal to $2πN$ (where $N$ is the number of revolutions of the body), find the average time period of the body.
$\sqrt{\dfrac{4I}{Nτ}}$ | |
$\sqrt{\dfrac{2πI}{Nτ}}$ | |
$\sqrt{\dfrac{πI}{Nτ}}$ | |
$\sqrt{\dfrac{8πI}{Nτ}}$ | |
$\sqrt{\dfrac{4πI}{Nτ}}$ |
Question 6 Explanation:
Angular acceleration $α=\dfrac{τ}{I}$
Using $α=\dfrac{τ}{I}, Δθ=2πN$ and $ω_o=0$ in $Δθ=ω_o t+\dfrac{1}{2} \ αt^2$
$2πN=\dfrac{1}{2} \dfrac{τ}{I} \ t^2$
$t=\sqrt{\dfrac{4πNI}{τ}}$
For one revolution,
$\dfrac{t}{N}=\sqrt{\dfrac{4πI}{Nτ}}$
Using $α=\dfrac{τ}{I}, Δθ=2πN$ and $ω_o=0$ in $Δθ=ω_o t+\dfrac{1}{2} \ αt^2$
$2πN=\dfrac{1}{2} \dfrac{τ}{I} \ t^2$
$t=\sqrt{\dfrac{4πNI}{τ}}$
For one revolution,
$\dfrac{t}{N}=\sqrt{\dfrac{4πI}{Nτ}}$
Question 7 |
Four particles of mass m each are placed at the corners of a rectangle of length $a$ and width $b$. What is the moment of inertia of the system about an axis passing through one of the corners and perpendicular to the plane of the rectangle?
$2m(a^2+b^2 )$ | |
$m(a^2+b^2 )$ | |
$2m(2a^2+b^2 )$ | |
$2m(a^2+2b^2 )$ | |
$3m(a^2+b^2 )$ |
Question 7 Explanation:
The system described in the question is shown below:
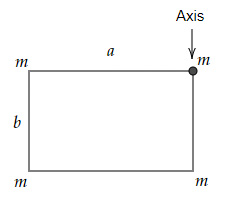
The distance of mass m to the left of the axis $=a$
The distance of mass m to the bottom of the axis $=b$
The distance of mass m on the diagonally opposite corner $=\sqrt{a^2+b^2}$
Moment of inertia $I=∑mr^2$
$=m(0)+m(a^2 )+m(b^2 )+m(a^2+b^2 )$
$=2m(a^2+b^2 )$

The distance of mass m to the left of the axis $=a$
The distance of mass m to the bottom of the axis $=b$
The distance of mass m on the diagonally opposite corner $=\sqrt{a^2+b^2}$
Moment of inertia $I=∑mr^2$
$=m(0)+m(a^2 )+m(b^2 )+m(a^2+b^2 )$
$=2m(a^2+b^2 )$
Question 8 |
Find the angular acceleration of the pulley having a moment of inertia of 0.1 kgm^2 in the figure below.
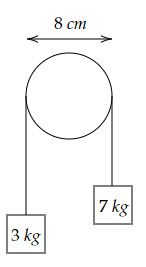
(Assume the rope does not slip on the pulley.)

(Assume the rope does not slip on the pulley.)
$11.8 \ rad/s^2$ | |
$12.5 \ rad/s^2$ | |
$13.7 \ rad/s^2$ | |
$9.8 \ rad/s^2$ | |
$8.7 \ rad/s^2 $ |
Question 8 Explanation:
From the free body diagrams of the system,
$T_1-3g=3a … (1)$
$7g-T_2=7a … (2)$
$(T_2-T_1 )×0.04=0.1α … (3)$
$a=0.04α … (4)$
Using $(1), (2)$ and $(3)$
$(7g-7a)-(3g+3a)=2.5α$
Using $(4)$ and simplifying gives,
$4g-0.4α=2.5α$
$α=13.7 \ rad/s^2$
$T_1-3g=3a … (1)$
$7g-T_2=7a … (2)$
$(T_2-T_1 )×0.04=0.1α … (3)$
$a=0.04α … (4)$
Using $(1), (2)$ and $(3)$
$(7g-7a)-(3g+3a)=2.5α$
Using $(4)$ and simplifying gives,
$4g-0.4α=2.5α$
$α=13.7 \ rad/s^2$
Question 9 |
A solid cylinder of mass $2.4 \ kg$ and radius $0.5 \ m$ is rolling on a horizontal surface without slipping. The angular velocity of the cylinder is $4 \ rad/s$. What is the total kinetic energy of the cylinder?
$8.3 \ J$ | |
$7.9 \ J$ | |
$7.2 \ J$ | |
$5.4 \ J$ | |
$6.6 \ J$ |
Question 9 Explanation:
Total $KE=\dfrac{1}{2} MV_{center}^2+\dfrac{1}{2} I_{cylinder} ω^2$
Using $V_{center}=ωR$ and $I_{cylinder}=\dfrac{1}{2} MR^2$ in the above equation gives,
Total $KE=\dfrac{1}{2} Mω^2 R^2+\dfrac{1}{4} Mω^2 R^2=\dfrac{3}{4} Mω^2 R^2$
Using $M=2.4 \ kg, ω=4 \ rad/s$ and $R=0.5 \ m$ gives,
Total $KE=\dfrac{3}{4}×2.4×4^2×(0.5)^2=7.2 \ J$
Using $V_{center}=ωR$ and $I_{cylinder}=\dfrac{1}{2} MR^2$ in the above equation gives,
Total $KE=\dfrac{1}{2} Mω^2 R^2+\dfrac{1}{4} Mω^2 R^2=\dfrac{3}{4} Mω^2 R^2$
Using $M=2.4 \ kg, ω=4 \ rad/s$ and $R=0.5 \ m$ gives,
Total $KE=\dfrac{3}{4}×2.4×4^2×(0.5)^2=7.2 \ J$
Question 10 |
A non-uniform rod of mass density $ρ(x)=2Ax \ g/cm$ can rotate about point $Y$, as shown below.
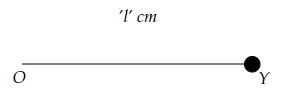
What is the moment of inertia of the rod about point $Y$?
(Here, $x$ is the distance from the origin $O$, and $A$ is a positive constant)
$\dfrac{Al^3}{2}$ | |
$\dfrac{Al^4}{6}$ | |
$\dfrac{5Al^4}{6}$ | |
$\dfrac{Al^2}{12}$ | |
$\dfrac{Al^4}{4}$ |
Question 10 Explanation:
$I=\int r^2 \ dm$
Using $dm=ρ(x)dx $ and $ r=(l-x)$ gives,
$I=\int_0^l ρ(x) (l-x)^2 \ dx$
$=\int_0^l 2Ax(l-x)^2 \ dx$
$=2A\int_0^l x(l^2-2xl+x^2 ) \ dx$
$=2A\int_0^l (l^2 x-2x^2 l+x^3 ) \ dx$
$=2A \left( \dfrac{l^2 x^2}{2}-\dfrac{2}{3} x^3 l+ \ \dfrac{x^4}{4} \right) |_0^l$
$=2A \left( \dfrac{l^4}{2} - \dfrac{2l^4}{3}+\dfrac{l^4}{4}\right)$
$=\dfrac{Al^4}{6}$
Using $dm=ρ(x)dx $ and $ r=(l-x)$ gives,
$I=\int_0^l ρ(x) (l-x)^2 \ dx$
$=\int_0^l 2Ax(l-x)^2 \ dx$
$=2A\int_0^l x(l^2-2xl+x^2 ) \ dx$
$=2A\int_0^l (l^2 x-2x^2 l+x^3 ) \ dx$
$=2A \left( \dfrac{l^2 x^2}{2}-\dfrac{2}{3} x^3 l+ \ \dfrac{x^4}{4} \right) |_0^l$
$=2A \left( \dfrac{l^4}{2} - \dfrac{2l^4}{3}+\dfrac{l^4}{4}\right)$
$=\dfrac{Al^4}{6}$
Question 11 |
The moment of inertia of a solid sphere of mass $M$ and radius $R$ about an axis passing through its center is equal to $ \dfrac{2}{5} \ MR^2$. What would be the moment of inertia for an axis tangent to the sphere?
$\dfrac{2}{5} \ MR^2$ | |
$\dfrac{3}{5} \ MR^2$ | |
$\dfrac{4}{5} \ MR^2$ | |
$\dfrac{7}{5} \ MR^2$ | |
$\dfrac{8}{5} \ MR^2$ |
Question 11 Explanation:
From parallel axis theorem,
$I_{tan}=I_{cm}+Md^2$
Using $I_{cm}=\dfrac{2}{5} \ MR^2$ and $d=R$
$I_{tan}=\dfrac{2}{5} \ MR^2+MR^2=\dfrac{7}{5} \ MR^2$
$I_{tan}=I_{cm}+Md^2$
Using $I_{cm}=\dfrac{2}{5} \ MR^2$ and $d=R$
$I_{tan}=\dfrac{2}{5} \ MR^2+MR^2=\dfrac{7}{5} \ MR^2$
Question 12 |
The diagram below shows the directions in which two particles of mass $m$ each move in an $x-y$ plane.
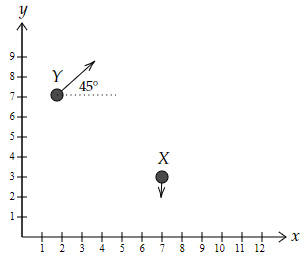
The magnitude of the velocities of the two particles, $X$ and $Y$, are $5 \ m/s$ and $6 \ m/s$, respectively. Determine the angular momentum of $X$ with respect to $Y$. (Hint: What is the velocity of $X$ with respect to $Y$?)
$(-34.96m) k ̂ \ m/s$ | |
$(-69.62m) k ̂ \ m/s$ | |
$(-39.42m) k ̂ \ m/s$ | |
$(-36.63m) k ̂ \ m/s$ | |
$(-63.16m) k ̂ \ m/s$ |
Question 12 Explanation:
Velocity of $X=-5\skew{5}\hat{j} \ m/s$
Velocity of $Y=6(\cos 45° \skew{2}\hat{i} + \sin 45° \skew{5}\hat{j} )=3\sqrt{2} (\skew{2}\hat{i}+j ̂ ) \ m/s$
Velocity of $X$ with respect to $Y=-5\skew{5}\hat{j}-3\sqrt{2} (\skew{2}\hat{i}+\skew{5}\hat{j})=-(4.24\skew{2}\hat{i}+9.24\skew{5}\hat{j} ) \ m/s$
Position of $X$ with respect to $Y =(7\skew{2}\hat{i}+3\skew{5}\hat{j} )-(2\skew{2}\hat{i}+7\skew{5}\hat{j} )=(5\skew{2}\hat{i}-4\skew{5}\hat{j} ) \ m/s$
Angular momentum $\overrightarrow{L}=m(\overrightarrow{r}×\overrightarrow{v})$
$=-m(5×9.24+4×4.24) k ̂ $
$=m(-63.16) k ̂ \ m/s$
Velocity of $Y=6(\cos 45° \skew{2}\hat{i} + \sin 45° \skew{5}\hat{j} )=3\sqrt{2} (\skew{2}\hat{i}+j ̂ ) \ m/s$
Velocity of $X$ with respect to $Y=-5\skew{5}\hat{j}-3\sqrt{2} (\skew{2}\hat{i}+\skew{5}\hat{j})=-(4.24\skew{2}\hat{i}+9.24\skew{5}\hat{j} ) \ m/s$
Position of $X$ with respect to $Y =(7\skew{2}\hat{i}+3\skew{5}\hat{j} )-(2\skew{2}\hat{i}+7\skew{5}\hat{j} )=(5\skew{2}\hat{i}-4\skew{5}\hat{j} ) \ m/s$
Angular momentum $\overrightarrow{L}=m(\overrightarrow{r}×\overrightarrow{v})$
$=-m(5×9.24+4×4.24) k ̂ $
$=m(-63.16) k ̂ \ m/s$
Question 13 |
Questions 13 and 14 are based on the below information:
A torque $τ(t) = 6t^2$ acts on a thin disc of moment of inertia $3 \ kgm^2$. The disc moves about an axis, passing through its center of mass and perpendicular to the plane of the disc.
What is the change in the angular momentum of the disc when it moves from time $t=2 \ s$ to $t=5 \ s$?
$207 \ kgm^2/s$ | |
$216 \ kgm^2/s$ | |
$234 \ kgm^2/s$ | |
$125 \ kgm^2/s$ | |
$192 \ kgm^2/s$ |
Question 13 Explanation:
$ΔL=\intτ(t)dt$
Thus,
$ΔL=\int_2^5 6t^2 \ dt$
$=6\int_2^5 t^2 \ dt$
$=6 \dfrac{t^3}{3} |_2^5$
$=2 (5^3-2^3 )$
$=234 \ kgm^2/s $
Thus,
$ΔL=\int_2^5 6t^2 \ dt$
$=6\int_2^5 t^2 \ dt$
$=6 \dfrac{t^3}{3} |_2^5$
$=2 (5^3-2^3 )$
$=234 \ kgm^2/s $
Question 14 |
A torque $τ(t) = 6t^2$ acts on a thin disc of moment of inertia $3 \ kgm^2$. The disc moves about an axis, passing through its center of mass and perpendicular to the plane of the disc.
If the disc was momentarily at rest at time $t=2 \ s$, what is the angular displacement of the disc in the time interval $t=2 \ s$ to $t=5 \ s$?
$92.5 \ rad$ | |
$85.5 \ rad$ | |
$99.8 \ rad$ | |
$82.7 \ rad$ | |
$88.2 \ rad$ |
Question 14 Explanation:
$α(t)=\dfrac{τ(t)}{I}= 2t ^2$
$ω(t)=\int 2t^2 \ dt$
$=\dfrac{2}{3} t^3+C$
Using $ω(2)=0 \ rad/s$ gives $C=-\dfrac{16}{3} $
$θ(t)=\int \dfrac{2}{3} t^3-\dfrac{16}{3} \ dt $
$=\dfrac{1}{6} t^4- \dfrac{16}{3} t+C'$
$Δθ=θ(5)-θ(2)=\dfrac{1}{6} (5^4-2^4 )-\dfrac{16}{3}(5-2)$
$=85.5 \ rad $
$ω(t)=\int 2t^2 \ dt$
$=\dfrac{2}{3} t^3+C$
Using $ω(2)=0 \ rad/s$ gives $C=-\dfrac{16}{3} $
$θ(t)=\int \dfrac{2}{3} t^3-\dfrac{16}{3} \ dt $
$=\dfrac{1}{6} t^4- \dfrac{16}{3} t+C'$
$Δθ=θ(5)-θ(2)=\dfrac{1}{6} (5^4-2^4 )-\dfrac{16}{3}(5-2)$
$=85.5 \ rad $
Question 15 |
Two solid discs are rotating about a common axis of rotation at speeds $8.5 \ rad/s$ and $-12.5 \ rad/s$. The masses of the discs are $4 \ kg$ and $3 \ kg$, respectively. The radius of both the discs is the same and is equal to $20 \ cm$.
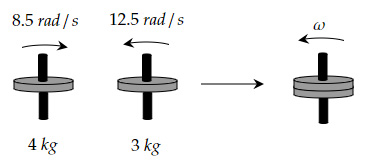
If the two discs are combined to rotate together as shown in the diagram above, then what is the common angular velocity of the two discs?
(Hint: No external torque is needed to achieve this)
$-0.50 \ rad/s$ | |
$3.20 \ rad/s$ | |
$0.25 \ rad/s$ | |
$1.75 \ rad/s$ | |
$-1.35 \ rad/s$ |
Question 15 Explanation:
Before the discs are combined,
Net Angular Momentum $=I_1 ω_1+I_2 ω_2$
$=\dfrac{1}{2} \ m_1 r^2 ω_1+\dfrac{1}{2} \ m_2 r^2 ω_2$
$=\dfrac{1}{2} \ r^2 (m_1 ω_1+m_2 ω_2 )$
$=\dfrac{1}{2} \ (0.2^2 )(4×8.5-3×12.5)$
$=-0.07 \ kgm^2/s$
After the discs are combined,
Net Angular Momentum $=Iω$
$=\dfrac{1}{2} \ mr^2 \ ω $
$=\dfrac{1}{2} (7)(0.2^2)ω$
$=0.14ω$
$=-0.07$
Thus, $ω=-0.50 \ rad/s$ ($-$ sign shows the velocity is anticlockwise)
Net Angular Momentum $=I_1 ω_1+I_2 ω_2$
$=\dfrac{1}{2} \ m_1 r^2 ω_1+\dfrac{1}{2} \ m_2 r^2 ω_2$
$=\dfrac{1}{2} \ r^2 (m_1 ω_1+m_2 ω_2 )$
$=\dfrac{1}{2} \ (0.2^2 )(4×8.5-3×12.5)$
$=-0.07 \ kgm^2/s$
After the discs are combined,
Net Angular Momentum $=Iω$
$=\dfrac{1}{2} \ mr^2 \ ω $
$=\dfrac{1}{2} (7)(0.2^2)ω$
$=0.14ω$
$=-0.07$
Thus, $ω=-0.50 \ rad/s$ ($-$ sign shows the velocity is anticlockwise)
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 15 questions to complete.
|
List |
Next Practice Test:
Unit 6: Oscillations >>
AP Physics C Mechanics Main Menu >>
