Our unit 4 practice test for AP Physics C Mechanics reviews the concepts of center of mass for discrete and continuous systems, kinematical quantities like position, velocity, and acceleration related to the center of mass of a system, the conservation of linear momentum for a system of particles and types of collisions.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
Three masses, $m, 2m,$ and $3m$ are at coordinates $(a,0), (4a,0),$ and $(-a,0)$, respectively. What are the coordinates of the center of mass of the system?
$(a,0)$ | |
$(0,a)$ | |
$(2a,0)$ | |
$(3a,0)$ | |
$(-2a,0)$ |
Question 1 Explanation:
x coordinate of the center of mass
$=\dfrac{∑mx}{∑m} $
$=\dfrac{m×a+2m×4a+3m×-a}{m+2m+3m}$
$=\dfrac{6ma}{6m}$
$=a$
Since the y coordinate for each mass is $0$
The coordinates of the center of mass of the system are $(a,0)$
$=\dfrac{∑mx}{∑m} $
$=\dfrac{m×a+2m×4a+3m×-a}{m+2m+3m}$
$=\dfrac{6ma}{6m}$
$=a$
Since the y coordinate for each mass is $0$
The coordinates of the center of mass of the system are $(a,0)$
Question 2 |
A system of three identical particles of mass $1 \ kg$ each are moving, as shown in the diagram below.
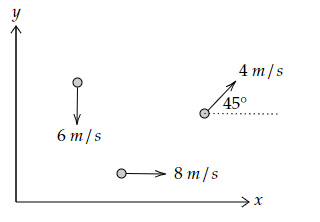
What is the net momentum of the system of these three particles?
$(10.00 \skew{2.3}\hat{i} -4.00\skew{4.5}\hat{j} ) \ kgm/s$ | |
$(10.83 \skew{2.3}\hat{i} -6.00\skew{4.5}\hat{j} ) \ kgm/s$ | |
$(12.33 \skew{2.3}\hat{i} +4.29\skew{4.5}\hat{j} ) \ kgm/s$ | |
$(10.83 \skew{2.3}\hat{i} -3.17\skew{4.5}\hat{j} ) \ kgm/s$ | |
$(11.22\skew{2.3}\hat{i} -3.17\skew{4.5}\hat{j} ) \ kgm/s$ |
Question 2 Explanation:
Velocities of the three particles are as shown below:
$\overrightarrow{v}_1=-6\skew{5}\hat{j} \ m/s, \overrightarrow{v}_2=8\skew{2}\hat{i} \ m/s$ and
$\overrightarrow{v}_3=(4 \cos45° \skew{2}\hat{i} + 4 \sin45° \skew{5}\hat{j} ) \ m/s$
Simplifying $\overrightarrow{v}_3$ gives $(2√2 \skew{2}\hat{i} +2√2 \skew{5}\hat{j} ) \ m/s$
Momentum of each particle is equal to its velocity as $m=1 \ kg$
Net momentum $=\overrightarrow{p}_1+\overrightarrow{p}_2+\overrightarrow{p}_3$
$=(-6\skew{5}\hat{j}+8\skew{2}\hat{i}+2 \sqrt{2}
\skew{2}\hat{i}+2 \sqrt{2} \skew{5}\hat{j} ) \ kgm/s$
$=(10.83\skew{2}\hat{i}-3.17\skew{5}\hat{j} ) \ kgm/s $
$\overrightarrow{v}_1=-6\skew{5}\hat{j} \ m/s, \overrightarrow{v}_2=8\skew{2}\hat{i} \ m/s$ and
$\overrightarrow{v}_3=(4 \cos45° \skew{2}\hat{i} + 4 \sin45° \skew{5}\hat{j} ) \ m/s$
Simplifying $\overrightarrow{v}_3$ gives $(2√2 \skew{2}\hat{i} +2√2 \skew{5}\hat{j} ) \ m/s$
Momentum of each particle is equal to its velocity as $m=1 \ kg$
Net momentum $=\overrightarrow{p}_1+\overrightarrow{p}_2+\overrightarrow{p}_3$
$=(-6\skew{5}\hat{j}+8\skew{2}\hat{i}+2 \sqrt{2}
\skew{2}\hat{i}+2 \sqrt{2} \skew{5}\hat{j} ) \ kgm/s$
$=(10.83\skew{2}\hat{i}-3.17\skew{5}\hat{j} ) \ kgm/s $
Question 3 |
A sphere of mass $2 \ kg$ is dropped from a height of $2 \ m$. On collision with the floor, the sphere rebounds with a speed of $3 \ m/s$. The magnitude of change in the momentum of the sphere is,
$9.32 \ kgm/s$ | |
$18.64 \ kgm/s$ | |
$15.24 \ kgm/s$ | |
$22.78 \ kgm/s$ | |
$20.13 \ kgm/s$ |
Question 3 Explanation:
Using $u=0 \ m/s$ in the equation $v^2=u^2+2gh$ gives the velocity of the sphere before collision as,
$v_b=\sqrt{2gh}$
$=\sqrt{2×10×2}$
$=6.32 m/s$ (downward)
Velocity after collision $v_a=3 \ m/s$ (upward)
Change in the velocity $=\overrightarrow{v}_a-\overrightarrow{v} b$
$=3-(-6.32)$
$=9.32 \ m/s$ (upward)
Magnitude of change in the momentum of the sphere $=2×9.32=18.64 \ kgm/s$
$v_b=\sqrt{2gh}$
$=\sqrt{2×10×2}$
$=6.32 m/s$ (downward)
Velocity after collision $v_a=3 \ m/s$ (upward)
Change in the velocity $=\overrightarrow{v}_a-\overrightarrow{v} b$
$=3-(-6.32)$
$=9.32 \ m/s$ (upward)
Magnitude of change in the momentum of the sphere $=2×9.32=18.64 \ kgm/s$
Question 4 |
Two particles of masses 1.5 kg and 1.25 kg are moving along different directions, as shown below.
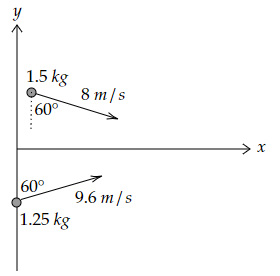
After the collision, they combine and move with velocity $\overrightarrow{V}$. Find the magnitude of $\overrightarrow{V}$.
$4.34 \ m/s$ | |
$3.67 \ m/s$ | |
$11.10 \ m/s$ | |
$8.22 \ m/s$ | |
$7.55 \ m/s$ |
Question 4 Explanation:
Momentum of particle of mass $1.5 \ kg$ before collision
$=1.5(8 \sin 60° \skew{2}\hat{i} -8 \cos 60° \skew{5}\hat{j} )$
$=12(\dfrac{\sqrt{3}}{2} \skew{2}\hat{i} - \dfrac{1}{2} \skew{5}\hat{j} ) \ kgm/s$
Momentum of particle of mass $1.25 \ kg$ before collision
$=1.25(9.6 \sin60° \skew{2}\hat{i} +9.6 \cos 60° \skew{5}\hat{j} )$
$=12(\dfrac{\sqrt{3}}{2} \skew{2}\hat{i} +\dfrac{1}{2} \skew{5}\hat{j} ) \ kgm/s$
Total momentum before collision
$=12\sqrt{3} \skew{2}\hat{i} \ kgm/s$
Total momentum after collision
$=2.75 \overrightarrow{V} kgm/s$
Thus, $2.75 \overrightarrow{V}=12 \sqrt{3} \skew{2}\hat{i}$
$\overrightarrow{V} =7.55\skew{2}\hat{i} \ m/s $
Speed $=V=7.55 \ m/s$
$=1.5(8 \sin 60° \skew{2}\hat{i} -8 \cos 60° \skew{5}\hat{j} )$
$=12(\dfrac{\sqrt{3}}{2} \skew{2}\hat{i} - \dfrac{1}{2} \skew{5}\hat{j} ) \ kgm/s$
Momentum of particle of mass $1.25 \ kg$ before collision
$=1.25(9.6 \sin60° \skew{2}\hat{i} +9.6 \cos 60° \skew{5}\hat{j} )$
$=12(\dfrac{\sqrt{3}}{2} \skew{2}\hat{i} +\dfrac{1}{2} \skew{5}\hat{j} ) \ kgm/s$
Total momentum before collision
$=12\sqrt{3} \skew{2}\hat{i} \ kgm/s$
Total momentum after collision
$=2.75 \overrightarrow{V} kgm/s$
Thus, $2.75 \overrightarrow{V}=12 \sqrt{3} \skew{2}\hat{i}$
$\overrightarrow{V} =7.55\skew{2}\hat{i} \ m/s $
Speed $=V=7.55 \ m/s$
Question 5 |
The net force acting on a system of interacting particles is $0 \ N$. Which of the below statements is TRUE regarding the system?
The velocity of the center of mass of the system changes with time | |
The force between any two particles within the system is also zero | |
The center of mass of the system can move but its time average must be zero | |
The sum of all internal forces must be 0 N irrespective of the external forces | |
The momentum of each individual particle is conserved |
Question 5 Explanation:
Option A → Velocity cannot change with time if net force is $0 \ N$
Option B → The force between any two particles may or may not be zero
Option C → The center of mass of the system can move with a fixed speed and so time average cannot be zero
Option D → The internal forces cancel in pairs and so the net internal force is $0 \ N$ and is independent of the external force(s)
Option E → The momentum of the system of particles is conserved and not for each individual particle
Option B → The force between any two particles may or may not be zero
Option C → The center of mass of the system can move with a fixed speed and so time average cannot be zero
Option D → The internal forces cancel in pairs and so the net internal force is $0 \ N$ and is independent of the external force(s)
Option E → The momentum of the system of particles is conserved and not for each individual particle
Question 6 |
An object moves due to force f(t) acting on it. Calculate the impulse on the object from time $t=0 \ s$ to $t=2 \ s$ if $f(t)=2e^{-t}$.
$2.84 \ kgm/s$ | |
$1.72 \ kgm/s$ | |
$2.46 \ kgm/s$ | |
$2.10 \ kgm/s$ | |
$1.32 \ kgm/s$ |
Question 6 Explanation:
$J=\int f(t) \ dt$
$=\int _0^2 2e^{-t} \ dt$
$=-2 (e^{-t}) |_0^2$
$=-2(e^{-2}-1)$
$=1.72 \ kgm/s $
$=\int _0^2 2e^{-t} \ dt$
$=-2 (e^{-t}) |_0^2$
$=-2(e^{-2}-1)$
$=1.72 \ kgm/s $
Question 7 |
A projectile of mass $4 \ kg$ falling vertically down explodes in mid-air. The projectile breaks into three parts, as shown below.
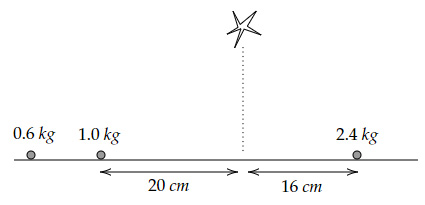
How far from the original line of motion does the $0.6 \ kg$ part fall?
$30.67 \ cm$ | |
$24.77 \ cm$ | |
$29.18 \ cm$ | |
$33.23 \ cm$ | |
$38.11 \ cm$ |
Question 7 Explanation:
The center of mass of the projectile falls straight down irrespective of the explosion (which is due to internal forces)
Assume the projectile is falling vertically down along the line $x=0$
$0=1×(-20)+0.6×d+2.4×16$
$0=-20+38.4+0.6d $
$d=-30.67 \ cm$
($-$ sign shows that it is on the left of the original line of motion)
Assume the projectile is falling vertically down along the line $x=0$
$0=1×(-20)+0.6×d+2.4×16$
$0=-20+38.4+0.6d $
$d=-30.67 \ cm$
($-$ sign shows that it is on the left of the original line of motion)
Question 8 |
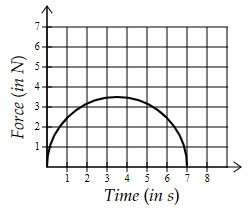
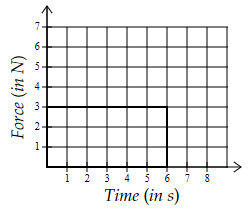
Which force-time graph shows the largest momentum change?
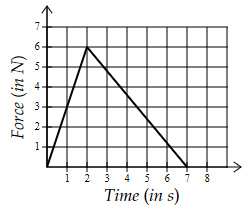 | |
 | |
 | |
 | |
 |
Question 8 Explanation:
Area under the curve is equal to the momentum change
Option A $→$ Area $=\dfrac{1}{2}×7×6=21 \ Ns$
Option B $→$ Area $=\dfrac{1}{2}×π×3.5^2=19.24 \ Ns$
Option C $→$ Area $=3×6=18 \ Ns$
Option D $→$ Area $=\dfrac{1}{2}×3×1+1×4+\dfrac{1}{2}×1×3=7 \ Ns$
Option E $→$ Area $=\dfrac{1}{2}×(1+6)×4+1×6+\dfrac{1}{2}×6×1=23 \ Ns$
Largest momentum change is for graph E
Option A $→$ Area $=\dfrac{1}{2}×7×6=21 \ Ns$
Option B $→$ Area $=\dfrac{1}{2}×π×3.5^2=19.24 \ Ns$
Option C $→$ Area $=3×6=18 \ Ns$
Option D $→$ Area $=\dfrac{1}{2}×3×1+1×4+\dfrac{1}{2}×1×3=7 \ Ns$
Option E $→$ Area $=\dfrac{1}{2}×(1+6)×4+1×6+\dfrac{1}{2}×6×1=23 \ Ns$
Largest momentum change is for graph E
Question 9 |
A non-uniform rod of linear density $ρ(x) = Ax^2$ (where $A$ is a positive constant) extends from $x=0$ to $x=L$. Find the center of mass of the rod.
$\dfrac{6}{7} \ L$ | |
$\dfrac{3}{5} \ L$ | |
$\dfrac{2}{5} \ L$ | |
$\dfrac{2}{3} \ L$ | |
$\dfrac{3}{4} \ L$ |
Question 9 Explanation:
Total mass $M=∫ρ(x)dx$
$=∫_0^L Ax^2 \ dx$
$=\dfrac{A}{3} (x^3) |_0^L$
$=\dfrac{A}{3} L^3$
Center of mass of the rod
$x_{cm}=\dfrac{1}{M} \int xdm$
$=\dfrac{1}{M} \int _0^L xρ(x)dx$
$=\dfrac{3}{AL^3} \int _0^L Ax^3 \ dx$
$=\dfrac{3}{AL^3} \dfrac{Ax^4}{4} |_0^L$
$=\dfrac{3}{4} \ L$
$=∫_0^L Ax^2 \ dx$
$=\dfrac{A}{3} (x^3) |_0^L$
$=\dfrac{A}{3} L^3$
Center of mass of the rod
$x_{cm}=\dfrac{1}{M} \int xdm$
$=\dfrac{1}{M} \int _0^L xρ(x)dx$
$=\dfrac{3}{AL^3} \int _0^L Ax^3 \ dx$
$=\dfrac{3}{AL^3} \dfrac{Ax^4}{4} |_0^L$
$=\dfrac{3}{4} \ L$
Question 10 |
Two balls of mass $m$ and $2m$, moving towards each other, suffer a head-on elastic collision. The velocities of the two balls before the collision are $-u$ and $3u$, respectively. What is the velocity of ball of mass $m$ after the collision if $2m$ continues to move in the same direction as before?
$\dfrac{4u}{3}$ | |
$\dfrac{6u}{5}$ | |
$\dfrac{13u}{3}$ | |
$-\dfrac{u}{3}$ | |
$\dfrac{5u}{3}$ |
Question 10 Explanation:
Assume ball of mass m goes to the left and $2m$ goes to the right
Total momentum before collision $=-mu+6mu=5mu$
Total kinetic energy before collision $=\dfrac{1}{2} \ mu^2+\dfrac{1}{2} \ 18mu^2=\dfrac{1}{2} \ 19mu^2$
Let the velocity of m be equal to v after the collision Speed of 2m after collision $=\dfrac{1}{2} (5u-v)$
Kinetic energy of 2m after the collision $=\dfrac{1}{8} \ 2m(5u-v)^2$
But from conservation of energy,
Kinetic energy of 2m after the collision $=\dfrac{1}{2} \ 19mu^2-\dfrac{1}{2} \ mv^2$
Solving for v gives,
$v=-u$ or $\dfrac{13u}{3}$
Rejecting $v=-u$ as it represents the original situation Thus, the velocity of m after the collision is $\dfrac{13u}{3}$
Total momentum before collision $=-mu+6mu=5mu$
Total kinetic energy before collision $=\dfrac{1}{2} \ mu^2+\dfrac{1}{2} \ 18mu^2=\dfrac{1}{2} \ 19mu^2$
Let the velocity of m be equal to v after the collision Speed of 2m after collision $=\dfrac{1}{2} (5u-v)$
Kinetic energy of 2m after the collision $=\dfrac{1}{8} \ 2m(5u-v)^2$
But from conservation of energy,
Kinetic energy of 2m after the collision $=\dfrac{1}{2} \ 19mu^2-\dfrac{1}{2} \ mv^2$
Solving for v gives,
$v=-u$ or $\dfrac{13u}{3}$
Rejecting $v=-u$ as it represents the original situation Thus, the velocity of m after the collision is $\dfrac{13u}{3}$
Question 11 |
A radioactive particle disintegrates into two smaller particles, as shown in the diagram below.
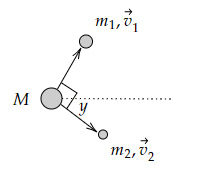
If the original particle was moving to the right with a speed of $v_1$, then what should be the size of angle $y$?
$y = \sin^{-1} \dfrac{ \dfrac{Mv_1}{m_2 v_2} } { \left( \dfrac {m_2 v_2}{m_1 v_1} \right)^2 -1 }$ | |
$y = \sin^{-1} \dfrac{ \dfrac{M}{m_1} } { \left( \dfrac {m_2 v_2}{m_1 v_1} \right)^2 +1 }$ | |
$y = \sin^{-1} \dfrac{ \dfrac{M}{m_1} } { \left( \dfrac {m_1 v_1}{m_2 v_2} \right)^2 -1 }$ | |
$y = \sin^{-1} \dfrac{ \dfrac{Mv_2}{m_1 v_1} } { \left( \dfrac {m_2 v_2}{m_1 v_1} \right)^2 +1 }$ | |
$y = \sin^{-1} \dfrac{ \dfrac{Mv_1}{m_1 v_2} } { \left( \dfrac {m_2 v_1}{m_1 v_2} \right)^2 +1 }$ |
Question 11 Explanation:
From momentum conservation,
$Mv_1=m_1 v_1 \cos (90°-y) +m_2 v_2$
$\cos y→Mv_1=m_1 v_1 \sin y+m_2 v_2 \cos y … (1)$
$0=-m_1 v_1 \sin (90°-y)+m_2 v_2$
$ \sin y→m_1 v_1 \cos y=m_2 v_2 \sin y … (2)$
Using $(1)$ and $(2)$,
$Mv_1=m_1 v_1 \sin y+\dfrac{(m_2 v_2 )^2}{(m_1 v_1} \sin y $
$Mv_1=\sin y \left( \dfrac{(m_2 v_2 )^2}{m_1 v_1 }+m_1 v_1 \right)$
$Mv_1=m_1 v_1 \sin y \left( \left( \dfrac{m_2 v_2}{m_1 v_1 }\right)^2+1\right)$
$\sin y = \dfrac{ \dfrac{Mv_1}{m_1 v_1} } { \left( \dfrac {m_2 v_2}{m_1 v_1} \right)^2 +1 }$
$y = \sin^{-1} \dfrac{ \dfrac{M}{m_1} } { \left( \dfrac {m_2 v_2}{m_1 v_1} \right)^2 +1 }$
$Mv_1=m_1 v_1 \cos (90°-y) +m_2 v_2$
$\cos y→Mv_1=m_1 v_1 \sin y+m_2 v_2 \cos y … (1)$
$0=-m_1 v_1 \sin (90°-y)+m_2 v_2$
$ \sin y→m_1 v_1 \cos y=m_2 v_2 \sin y … (2)$
Using $(1)$ and $(2)$,
$Mv_1=m_1 v_1 \sin y+\dfrac{(m_2 v_2 )^2}{(m_1 v_1} \sin y $
$Mv_1=\sin y \left( \dfrac{(m_2 v_2 )^2}{m_1 v_1 }+m_1 v_1 \right)$
$Mv_1=m_1 v_1 \sin y \left( \left( \dfrac{m_2 v_2}{m_1 v_1 }\right)^2+1\right)$
$\sin y = \dfrac{ \dfrac{Mv_1}{m_1 v_1} } { \left( \dfrac {m_2 v_2}{m_1 v_1} \right)^2 +1 }$
$y = \sin^{-1} \dfrac{ \dfrac{M}{m_1} } { \left( \dfrac {m_2 v_2}{m_1 v_1} \right)^2 +1 }$
Question 12 |
An isolated system of four identical interacting particles is moving steadily along the $+x$ direction. The velocity of the center of mass of the system is equal to $1 \ m/s$. If the velocity of three particles is ($2\skew{2.5}\hat{i} +2\skew{4}\hat{j}) \ m/s, (\skew{2.5}\hat{i} + 2\skew{4}\hat{j}) \ m/s,$ and $(-3\skew{2.5}\hat{i} - 5\skew{4}\hat{j}) \ m/s$, then what is the velocity of the fourth particle?
$(-\skew{4.5}\hat{j} ) \ m/s$ | |
$(\skew{2.3}\hat{i} + \skew{4.5}\hat{j} ) \ m/s$ | |
$(\skew{2.3}\hat{i} + 4\skew{4.5}\hat{j}) \ m/s$ | |
$(4\skew{2.3}\hat{i} +2 \skew{4.5}\hat{j}) \ m/s$ | |
$(4\skew{2.3}\hat{i} + \skew{4.5}\hat{j}) \ m/s$ |
Question 12 Explanation:
$M\overrightarrow{v}_{cm}=m_1 \overrightarrow{v}_1+m_2 \overrightarrow{v}_2+m_3 \overrightarrow{v}_3+m_4 \overrightarrow{v}_4$
$4m(\skew{2}\hat{i} )=m(2\skew{2}\hat{i} +2\skew{5}\hat{j} )+m(\skew{2}\hat{i} +2\skew{5}\hat{j} )$
$+m(-3\skew{2}\hat{i} -5\skew{5}\hat{j} )+m\overrightarrow{v}_4$
$4\skew{2}\hat{i} =(2\skew{2}\hat{i} +2\skew{5}\hat{j} )+(\skew{2}\hat{i} +2j ̂ )+(-3\skew{2}\hat{i} -5\skew{5}\hat{j} )+\overrightarrow{v}_4$
$\overrightarrow{v}_4=\left((-2-1+3+4) \skew{2}\hat{i} +(-2-2+5) \skew{5}\hat{j} \right) $
$\overrightarrow{v}_4=(4\skew{2}\hat{i} + \skew{5}\hat{j}) $
$4m(\skew{2}\hat{i} )=m(2\skew{2}\hat{i} +2\skew{5}\hat{j} )+m(\skew{2}\hat{i} +2\skew{5}\hat{j} )$
$+m(-3\skew{2}\hat{i} -5\skew{5}\hat{j} )+m\overrightarrow{v}_4$
$4\skew{2}\hat{i} =(2\skew{2}\hat{i} +2\skew{5}\hat{j} )+(\skew{2}\hat{i} +2j ̂ )+(-3\skew{2}\hat{i} -5\skew{5}\hat{j} )+\overrightarrow{v}_4$
$\overrightarrow{v}_4=\left((-2-1+3+4) \skew{2}\hat{i} +(-2-2+5) \skew{5}\hat{j} \right) $
$\overrightarrow{v}_4=(4\skew{2}\hat{i} + \skew{5}\hat{j}) $
Question 13 |
Questions 13, 14, and 15 are based on the below information:
A ball of mass $0.2 \ kg$ is moving towards a wall with a speed of $6.5 \ m/s$. It undergoes a partial inelastic collision and bounces back with a smaller velocity, as shown below.

What is the value of u if the ball loses 24% of its energy due to the collision?
$5.92 \ m/s$ | |
$5.43 \ m/s$ | |
$4.45 \ m/s$ | |
$5.67 \ m/s$ | |
$6.11 \ m/s$ |
Question 13 Explanation:
Kinetic energy before collision $=\dfrac{1}{2}×0.2×6.5^2 = 4.225 \ J$
Kinetic energy after collision $=76\%$ of $4.225 J=3.211 \ J$
$u=\sqrt{2×\dfrac{KE_{after}}{m}}$
Using $KE_{after}=3.211 \ J$ and $m=0.2 \ kg$ in the above equation gives,
$u=\sqrt{\dfrac{2×3.211}{0.2}} = 5.67 \ m/s$
Kinetic energy after collision $=76\%$ of $4.225 J=3.211 \ J$
$u=\sqrt{2×\dfrac{KE_{after}}{m}}$
Using $KE_{after}=3.211 \ J$ and $m=0.2 \ kg$ in the above equation gives,
$u=\sqrt{\dfrac{2×3.211}{0.2}} = 5.67 \ m/s$
Question 14 |
A ball of mass $0.2 \ kg$ is moving towards a wall with a speed of $6.5 \ m/s$. It undergoes a partial inelastic collision and bounces back with a smaller velocity, as shown below.

Calculate the average force $f_{avg}$ acting on the ball during the collision with the wall if the time of contact is $0.25 \ s$.
$9.74 \ N$ | |
$9.22 \ N$ | |
$8.56 \ N$ | |
$8.21 \ N$ | |
$10.41 \ N$ |
Question 14 Explanation:
Momentum before collision $=0.2×6.50=1.30 \ kgm/s $(right)
Momentum after collision $=0.2×5.67=1.134 \ kgm/s $(left)
Change in the momentum $Δp=1.134-(-1.30)=2.434 \ kgm/s$
Average force acting on the ball $f_{avg}=\dfrac{2.434}{0.25}=9.74 \ N$
Momentum after collision $=0.2×5.67=1.134 \ kgm/s $(left)
Change in the momentum $Δp=1.134-(-1.30)=2.434 \ kgm/s$
Average force acting on the ball $f_{avg}=\dfrac{2.434}{0.25}=9.74 \ N$
Question 15 |
A ball of mass $0.2 \ kg$ is moving towards a wall with a speed of $6.5 \ m/s$. It undergoes a partial inelastic collision and bounces back with a smaller velocity, as shown below.

If the actual variation in force is given in the graph below, then what is the value of $f_{max}$?
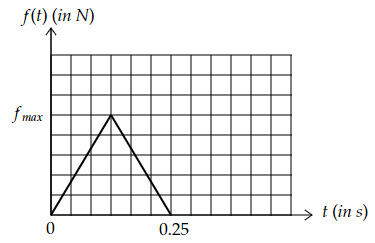
$18.92 \ N$ | |
$12.56 \ N$ | |
$9.68 \ N$ | |
$22.06 \ N$ | |
$19.47 \ N$ |
Question 15 Explanation:
Area under the curve = Change in the momentum of the ball
Area $= \dfrac{1}{2}×f_{max}×0.25=1/8×f_{max}$
Using $Δp=2.434 \ kgm/s$ gives,
$f_{max}=8×2.434=19.47 \ N $
Area $= \dfrac{1}{2}×f_{max}×0.25=1/8×f_{max}$
Using $Δp=2.434 \ kgm/s$ gives,
$f_{max}=8×2.434=19.47 \ N $
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 15 questions to complete.
|
List |
Next Practice Test:
Unit 5: Rotation >>
AP Physics C Mechanics Main Menu >>
