Unit 3 of AP Physics C Mechanics covers the basics of work, energy, and power. Also, problems on types of forces (conservative and non-conservative), work-energy theorem, types of energies, and energy conservation in isolated mechanical systems are considered.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
A boy pedals a cycle to reach a speed of $6 \ m/s$. The force needed to keep the cycle moving at the same speed is $40 \ N$. What is the power delivered by the boy to keep the cycle moving forward?
$460 \ W$ | |
$330 \ W$ | |
$196 \ W$ | |
$400 \ W$ | |
$240 \ W$ |
Question 1 Explanation:
Power delivered $=Fv \ \cosθ$
Using $v=6 \ m/s, F=40 \ N$ and $θ=0°$
Power delivered $=40×6×1$
$=240 \ W$
Using $v=6 \ m/s, F=40 \ N$ and $θ=0°$
Power delivered $=40×6×1$
$=240 \ W$
Question 2 |
A position-dependent force (in 1D) acts on an object of mass $m$. The graph shows the variation in the force as the object displaces from its initial position.
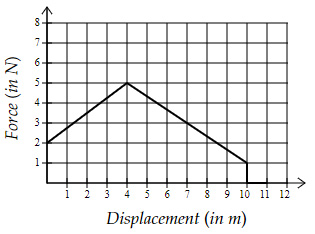
What is the total work done by the force on the object?
$32 \ J$ | |
$64 \ J$ | |
$50 \ J$ | |
$46 \ J$ | |
$38 \ J$ |
Question 2 Explanation:
Work done = Area under the curve $=A_I+A_{II} $

$A_I=\dfrac{1}{2}×(2+5)×4=14 \ J$
$A_{II}=\dfrac{1}{2}×(1+5)×6=18 \ J$
Total work done $=14+18=32 \ J$

$A_I=\dfrac{1}{2}×(2+5)×4=14 \ J$
$A_{II}=\dfrac{1}{2}×(1+5)×6=18 \ J$
Total work done $=14+18=32 \ J$
Question 3 |
A particle of mass $0.5 \ kg$ is at rest and is constrained to move parallel to the $y-axis$. If a force of $(10\skew{2.5}\hat{i} + 6\skew{4}\hat{j}) \ N$ starts acting on the object from $t=0 \ s$, what is the work done on the object from $t=0 \ s$ to $t=4 \ s$?
$724 \ J$ | |
$960 \ J$ | |
$576 \ J$ | |
$441 \ J$ | |
$660 \ J$ |
Question 3 Explanation:
Force acting in the $y$ direction $=6 \ N$
Acceleration of the object in the y direction $=\dfrac{6}{0.5}=12 \ m/s^2$
Displacement in the $y$ direction $=h$
And, $h=ut+\dfrac{1}{2} at^2$
Using $u=0 \ m/s, t=4 \ s$ and $a=12 \ m/s^2$
$h=0+\dfrac{1}{2}×12×4^2=96 \ m$
Work done $=F×h$
$=6×96$
$=576 \ J$
Acceleration of the object in the y direction $=\dfrac{6}{0.5}=12 \ m/s^2$
Displacement in the $y$ direction $=h$
And, $h=ut+\dfrac{1}{2} at^2$
Using $u=0 \ m/s, t=4 \ s$ and $a=12 \ m/s^2$
$h=0+\dfrac{1}{2}×12×4^2=96 \ m$
Work done $=F×h$
$=6×96$
$=576 \ J$
Question 4 |
A block at rest is pulled by a force acting at an angle of $60°$ to the horizontal. The block displaces by $23 \ m$ horizontally without being accelerated by the force. If the work done by the force is $230 \ J$, what is the force acting on the block?
$(17.3 \skew{2.3}\hat{i} + 20 \skew{4.5}\hat{j} ) \ N$ | |
$(10 \skew{2.3}\hat{i} + 17.3 \skew{4.5}\hat{j} ) \ N$ | |
$(20 \skew{2.3}\hat{i} +10 \skew{4.5}\hat{j} ) \ N$ | |
$(17.3 \skew{2.3}\hat{i} + 10 \skew{4.5}\hat{j} ) \ N$ | |
$(10 \skew{2.3}\hat{i} +20 \skew{4.5}\hat{j} ) \ N$ |
Question 4 Explanation:
The free body diagram for the object is:
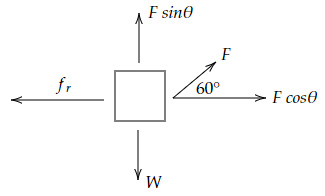
Work done on the object $W=F \ \cosθ×s$
Using $W=230 \ J, s=23 \ m$ and $θ=60°$
$230=F \ \cos 60°×23$
$F=20 \ N$
Thus, $ F_x=20 \ \cos60°=10 \ N$ and $F_y=20 \ \sin60°=17.3 \ N$
$\overrightarrow{F}=(10\skew{2}\hat{i} + 17.3 \skew{5}\hat{j} ) N$

Work done on the object $W=F \ \cosθ×s$
Using $W=230 \ J, s=23 \ m$ and $θ=60°$
$230=F \ \cos 60°×23$
$F=20 \ N$
Thus, $ F_x=20 \ \cos60°=10 \ N$ and $F_y=20 \ \sin60°=17.3 \ N$
$\overrightarrow{F}=(10\skew{2}\hat{i} + 17.3 \skew{5}\hat{j} ) N$
Question 5 |
A heavy block moving on a table decelerates due to the frictional force.

The block’s speed changes from $15 \ m/s$ to $3 \ m/s$ in $5 \ s$. If the weight of the block is equal to $100 \ N$, what is the coefficient of kinetic friction between the block and the table?
$0.17$ | |
$0.14$ | |
$0.19$ | |
$0.24$ | |
$0.22$ |
Question 5 Explanation:
Deceleration $a=\dfrac{3 - 15}{5}=-2.4 \ m/s^2$
Mass of the block $=\dfrac{100}{10}=10 \ kg$
Frictional force on the block $=ma=-24 \ N$
($-ive$ sign shows that the force is in the opposite direction that of the motion)
Using $f_r=24 \ N, N=W=100 \ N$ in $f_r=μ_k \ N$ gives,
$μ_k=\dfrac{24}{100}=0.24 $
Mass of the block $=\dfrac{100}{10}=10 \ kg$
Frictional force on the block $=ma=-24 \ N$
($-ive$ sign shows that the force is in the opposite direction that of the motion)
Using $f_r=24 \ N, N=W=100 \ N$ in $f_r=μ_k \ N$ gives,
$μ_k=\dfrac{24}{100}=0.24 $
Question 6 |
Two blocks are resting on a frictionless inclined plane, as shown below.

What is the change in the total kinetic energy of the two-block system when the left block reaches the pulley after being allowed to move from the above configuration?
(Here, $g$ is the acceleration due to gravity)
$2.4 \ g$ | |
$3 \ g$ | |
$1.2 \ g$ | |
$2 \ g$ | |
$2.8 \ g$ |
Question 6 Explanation:
Initial kinetic energy of the two-block system $=0$
Initial potential energy of the two-block system $=2×g×2+3×g×2=10 \ g$
New configuration of the two-block system is:
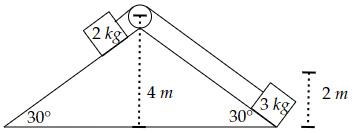
New potential energy of the two-block system $=2×g×4+3×g×0=8 \ g$
New kinetic energy of the two-block system
$=(10g+0)-8g=2 \ g$
Change in the kinetic energy of the two-block system $=2g-0=2 \ g$
Initial potential energy of the two-block system $=2×g×2+3×g×2=10 \ g$
New configuration of the two-block system is:

New potential energy of the two-block system $=2×g×4+3×g×0=8 \ g$
New kinetic energy of the two-block system
$=(10g+0)-8g=2 \ g$
Change in the kinetic energy of the two-block system $=2g-0=2 \ g$
Question 7 |
The net force acting on an object is given by the equation,
$f(x)=(2x+1) \ N$
What is the change in the kinetic energy of the system when the object moves from $x=2 \ m$ to $x=6 \ m$?
$24 \ J$
| |
$30 \ J$
| |
$44 \ J$
| |
$36 \ J$
| |
$18 \ J$ |
Question 7 Explanation:
Work done = Change in the kinetic energy of the system
Work done $=\int_{x=2}^{x=6} \ f(x)dx $
$=\int_{x=2}^{x=6} \ (2x+1)dx $
$= x^2+x |_2^6$
$=(6^2-2^2 )+(6-2) $
$=32+4$
$=36 \ J$
Work done $=\int_{x=2}^{x=6} \ f(x)dx $
$=\int_{x=2}^{x=6} \ (2x+1)dx $
$= x^2+x |_2^6$
$=(6^2-2^2 )+(6-2) $
$=32+4$
$=36 \ J$
Question 8 |
A toy of mass $0.2 \ kg$ is left from the top of a pre-determined track of height $h m$.

The track has a single circular loop of diameter $3 \ m$ after the curve. What is the minimum height from which the toy should be left so that it completes the circle without losing contact at any point on it?
$3.75 \ m$ | |
$3.00 \ m$ | |
$4.55 \ m$ | |
$3.45 \ m$ | |
$3.95 \ m$ |
Question 8 Explanation:
The minimum velocity (at the topmost point of the circular track) at which the toy can complete the track without falling down is:
$v=\sqrt{gr} \ $ thus $ \ v^2=1.5g$
From the conservation of energy,
$PE_{topmost}=PE_{top}+KE_{top} $
$0.2×g×h=0.2×g×3+0.5×0.2×1.5×g$
$0.2h=0.75→h=3.75 \ m$
$v=\sqrt{gr} \ $ thus $ \ v^2=1.5g$
From the conservation of energy,
$PE_{topmost}=PE_{top}+KE_{top} $
$0.2×g×h=0.2×g×3+0.5×0.2×1.5×g$
$0.2h=0.75→h=3.75 \ m$
Question 9 |
George sets a pendulum in motion from point $C$. The length of the pendulum is equal to $2 \ m$, and the mass attached to the pendulum is $0.5 \ kg$.

What is the tension force acting on the mass when it is at point $A$?
$9.89 \ N$ | |
$10.28 \ N$ | |
$7.99 \ N$ | |
$13.33 \ N$ | |
$11.21 \ N$ |
Question 9 Explanation:
Total energy of the pendulum at point $C=-0.5×10×2 \ \cos 60°=-5 \ J$
Total energy of the pendulum at point $A=\dfrac{1}{2} \ mv^2-mgr \ \cos 30°$
Since, total mechanical energy is a constant
$\dfrac{1}{2} \ mv^2=-5+0.5×10×2×\cos 30°=3.66 \ J$
$v^2=14.64 $
At point $A$,
$T=mg \ \cos 30° +\dfrac{mv^2}{r}$
$T=0.5×10×\dfrac{\sqrt{3}}{2}+\dfrac{0.5×14.64}{2}$
$T=7.99 \ N $
Total energy of the pendulum at point $A=\dfrac{1}{2} \ mv^2-mgr \ \cos 30°$
Since, total mechanical energy is a constant
$\dfrac{1}{2} \ mv^2=-5+0.5×10×2×\cos 30°=3.66 \ J$
$v^2=14.64 $
At point $A$,
$T=mg \ \cos 30° +\dfrac{mv^2}{r}$
$T=0.5×10×\dfrac{\sqrt{3}}{2}+\dfrac{0.5×14.64}{2}$
$T=7.99 \ N $
Question 10 |
Questions 10 and 11 are based on the below information:
A weird positional dependent frictional force acts on a block sliding down from the top of an inclined plane of slanting length $10 \ m$ and height $5 \ m$. The dependence of the frictional force on the position is given as $f_r (x)=A \sqrt{x} \ N$ where $A$ is $a$ constant and $x$ is the distance from the top of the inclined plane.
If the mass of the block is equal to $2 \ kg$, then what is the energy loss due to frictional force as the block slides down from the top to the bottom?
$33.01 \ A$ | |
$21.08 \ A$ | |
$22.52 \ A$ | |
$28.83 \ A$ | |
$19.02 \ A$ |
Question 10 Explanation:
Energy loss = Work done by the frictional force
Work done $=\int_0^{10} \ f_r (x) \ dx$
$=\int_0^{10} \ A \sqrt{x} \ dx$
$=A \int_0^{10} \ \sqrt{x} \ dx $
$=\dfrac{2A}{3}×10^{3/2}$
$=21.08 \ A$
Work done $=\int_0^{10} \ f_r (x) \ dx$
$=\int_0^{10} \ A \sqrt{x} \ dx$
$=A \int_0^{10} \ \sqrt{x} \ dx $
$=\dfrac{2A}{3}×10^{3/2}$
$=21.08 \ A$
Question 11 |
A weird positional dependent frictional force acts on a block sliding down from the top of an inclined plane of slanting length $10 \ m$ and height $5 \ m$. The dependence of the frictional force on the position is given as $f_r (x)=A \sqrt{x} \ N$ where $A$ is $a$ constant and $x$ is the distance from the top of the inclined plane.
If the velocity of the block at the bottom of the inclined plane is $\sqrt{21} \ m/s$, then what is the value $A$?
$2.95$ | |
$1.90$ | |
$4.20$ | |
$3.33$ | |
$3.75$ |
Question 11 Explanation:
Total energy at the top of the inclined plane
$=2×10×5=100 \ J$
Total energy at the bottom of the inclined plane
$=\dfrac{1}{2}×2×(\sqrt{21})^2=21 \ J$
Energy loss $=100-21=79 \ J$
$21.08A=79$
$→A=3.75$
$=2×10×5=100 \ J$
Total energy at the bottom of the inclined plane
$=\dfrac{1}{2}×2×(\sqrt{21})^2=21 \ J$
Energy loss $=100-21=79 \ J$
$21.08A=79$
$→A=3.75$
Question 12 |
A ball of mass m is used to push down a spring of length $l$ by $x$. The system is then allowed to move from this configuration.

10% of the total mechanical energy of the ball is lost by the time it reaches the topmost point of its trajectory. The height h that the ball rises is equal to,
(Assume the spring constant as $\dfrac{2mg}{l}$ and the energy transferred to the ball is 100%)
$\dfrac{0.9x^2}{l}-0.5 \ (l-x)$ | |
$\dfrac{0.9x^2}{l}+0.9 \ (x-l)$ | |
$\dfrac{1.2x^2}{l}+1.2 (l-x)$ | |
$\dfrac{0.9x^2}{l}+0.9 \ (l-x)$ | |
$\dfrac{0.5x^2}{l}+0.5 \ (l-x)$ |
Question 12 Explanation:
Initial energy of the ball $=\dfrac{1}{2} \ kx^2+mg \ (l-x)$
Final energy of the ball $=mgh$
Final energy of the ball $=90 \%$ of the initial energy
$mgh=0.9 \left(\dfrac{1}{2} kx^2+mg(l-x)\right) $
$h=0.9\left(\dfrac{1}{2} \ \dfrac{k}{mg} \ x^2+(l-x)\right) $
$h=\dfrac{0.9x^2}{l}+0.9(l-x) $
Final energy of the ball $=mgh$
Final energy of the ball $=90 \%$ of the initial energy
$mgh=0.9 \left(\dfrac{1}{2} kx^2+mg(l-x)\right) $
$h=0.9\left(\dfrac{1}{2} \ \dfrac{k}{mg} \ x^2+(l-x)\right) $
$h=\dfrac{0.9x^2}{l}+0.9(l-x) $
Question 13 |
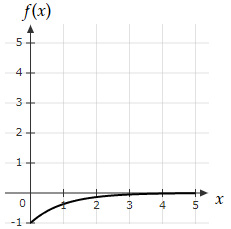
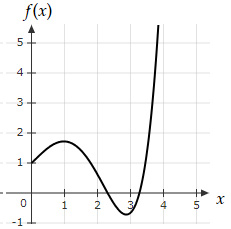
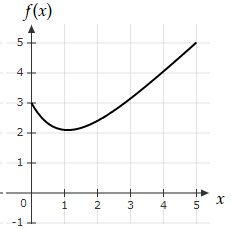
The potential energy of a 1D system is equal to $U(x)=-x \left(1+ \dfrac{2}{x} e^{-x} \right)$. Which of the below graphs shows the force $f$ as a function of the position x?
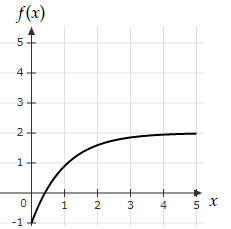 | |
 | |
 | |
 | |
 |
Question 13 Explanation:
$U(x)=-x \left(1+\dfrac{2}{x} e^{-x} \right) $
Simplifying the potential gives,
$U(x)=-x-2e^{-x}$
$f(x)=-\dfrac{dU}{dx}$
Thus, $f(x)=-\dfrac{d}{dx} (-x-2e^{-x} )$
$f(x)=-(-1+2e^{-x} )$
$f(x)=1-2e^{-x}$
Since $f(0)=-1$ and as $x→+∞, f(x)→1$
Which is true for Option E
Simplifying the potential gives,
$U(x)=-x-2e^{-x}$
$f(x)=-\dfrac{dU}{dx}$
Thus, $f(x)=-\dfrac{d}{dx} (-x-2e^{-x} )$
$f(x)=-(-1+2e^{-x} )$
$f(x)=1-2e^{-x}$
Since $f(0)=-1$ and as $x→+∞, f(x)→1$
Which is true for Option E
Question 14 |
A 1D system has a potential energy function, as shown below.
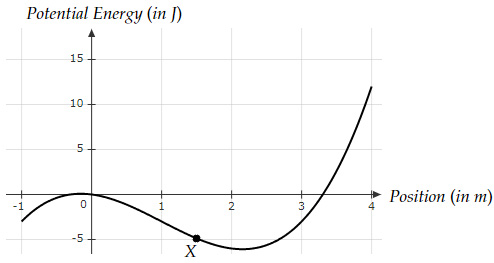
A particle of mass $1.2 \ kg$ is released with zero initial velocity and with an energy of $10 \ J$. Using the graph, determine the velocity of the particle at point $X$.
(Assume the total mechanical energy of the system is a constant)
$5 \ m/s$ | |
$4 \ m/s$ | |
$6 \ m/s$ | |
$8 \ m/s$ | |
$7 \ m/s$ |
Question 14 Explanation:
Total mechanical energy of the system $=10 \ J$
Total mechanical energy of the system at point
$X=-5+KE$
Thus, $KE=10+5=15 \ J$
$v=\sqrt{\dfrac{2×KE}{m}}$
$=\sqrt{\dfrac{2×15}{1.2}}$
$=\sqrt{25}$
$=5 \ m/s$
Total mechanical energy of the system at point
$X=-5+KE$
Thus, $KE=10+5=15 \ J$
$v=\sqrt{\dfrac{2×KE}{m}}$
$=\sqrt{\dfrac{2×15}{1.2}}$
$=\sqrt{25}$
$=5 \ m/s$
Question 15 |
A non-constant, non-conservative force $F(t)$ acts on a block, as shown below.
Here, $F(t)=\dfrac{4}{t + 1} \ N$ and $t≥0$.
What is the power delivered to the block as it goes from time $t=2 \ s$ to $t=5 \ s$?
(Hint: Use $P=∫_{t_1}^{t_2} F(t)a(t)dt)$
$4.50 \ W$ | |
$3.67 \ W$ | |
$3.33 \ W$ | |
$5.25 \ W$ | |
$6.20 \ W$ |
Question 15 Explanation:
Acceleration of the block $a(t)=\dfrac{F(t)}{m}=\dfrac{5}{t + 1}$
$P=\int_{t_1}^{t_2} F(t)a(t) \ dt$
$=\int_2^5 \dfrac{4}{t+1} \ \dfrac{5}{t+1} \ dt$
$=20\int_2^5 \dfrac{1}{(t+1)^2} \ dt$
$=20 \dfrac{(t+1)^{-1}}{-1} |_2^5$
$=-20\left( \dfrac{1}{6} - \dfrac{1}{3}\right)$
$=3.33 \ W$
$P=\int_{t_1}^{t_2} F(t)a(t) \ dt$
$=\int_2^5 \dfrac{4}{t+1} \ \dfrac{5}{t+1} \ dt$
$=20\int_2^5 \dfrac{1}{(t+1)^2} \ dt$
$=20 \dfrac{(t+1)^{-1}}{-1} |_2^5$
$=-20\left( \dfrac{1}{6} - \dfrac{1}{3}\right)$
$=3.33 \ W$
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 15 questions to complete.
|
List |
Next Practice Test:
Unit 4: Systems of Particles & Linear Momentum >>
AP Physics C Mechanics Main Menu >>
