Below is our AP Physics C unit 2 practice test. It covers Newton’s laws of motion and their application to solving problems with the help of free-body diagrams. Mathematical difficulty needed to solve the equations comprise of basic algebra, trigonometry, and a bit of calculus (Integration, differentiation and solving simple differential equations).
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
Two independent sources of force act on an object. The vector form of these forces is given below:
$\overrightarrow{F}_I = 2 \skew{2.5}\hat{i} + 7 \skew{4}\hat{j} \ N$ and $\overrightarrow{F}_{II} = 5 \skew{2.5}\hat{i} + 4 \skew{4}\hat{j} \ N$
What is the acceleration of the object, in $m/s^2$, if its mass is $4 \ kg$?
$ \dfrac{3}{4} (\skew{2.3}\hat{i} + \skew{4.5}\hat{j} ) $ | |
$ \dfrac{1}{6} (12 \skew{2.3}\hat{i} +10 \skew{4.5}\hat{j} )$ | |
$ \dfrac{1}{4} (11 \skew{2.3}\hat{i} +7 \skew{4.5}\hat{j} )$ | |
$ \dfrac{1}{4} (6 \skew{2.3}\hat{i} +9 \skew{4.5}\hat{j} ) $ | |
$ \dfrac{1}{4} (7 \skew{2.3}\hat{i} +11 \skew{4.5}\hat{j} )$ |
Question 1 Explanation:
Net force acting on the object
$=(2 \skew{2}\hat{i} +7 \skew{5}\hat{j} )+(5\skew{2}\hat{i}+4 \skew{5}\hat{j} )$
$=(7 \skew{2}\hat{i} +11 \skew{5}\hat{j} ) $
Acceleration of the object
$=\dfrac{1}{mass} × Force$
$=\dfrac{1}{4} (7 \skew{2}\hat{i} +11 \skew{5}\hat{j} ) $
$=(2 \skew{2}\hat{i} +7 \skew{5}\hat{j} )+(5\skew{2}\hat{i}+4 \skew{5}\hat{j} )$
$=(7 \skew{2}\hat{i} +11 \skew{5}\hat{j} ) $
Acceleration of the object
$=\dfrac{1}{mass} × Force$
$=\dfrac{1}{4} (7 \skew{2}\hat{i} +11 \skew{5}\hat{j} ) $
Question 2 |
Look at the below Atwood Machine with a frictionless pulley. Assume the string and the pulley are of negligible mass.
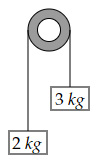
The system is released from rest. The acceleration of the $2 \ kg$ block is,
$2.5 \ m/s^2$ | |
$2.0 \ m/s^2$ | |
$3.6 \ m/s^2$ | |
$4.3 \ m/s^2$ | |
$5.4 \ m/s^2$ |
Question 2 Explanation:
The free body diagram of the two blocks is,
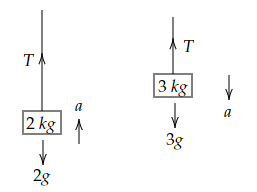
$T-2g=2a$ … (1)
$3g-T=3a$ … (2)
Adding (1) and (2),
$g = 5a → a = \dfrac{g}{5} =2 \ m/s^2 $

$T-2g=2a$ … (1)
$3g-T=3a$ … (2)
Adding (1) and (2),
$g = 5a → a = \dfrac{g}{5} =2 \ m/s^2 $
Question 3 |
A frictionless circular shaped ring has a small marble of mass $m$ fixed on it, as shown below.

The marble is set into motion at a uniform speed $u$. Which of the below forces keeps the marble moving at a uniform speed?
Friction between marble and the ring | |
Weight of the marble | |
Weight of the ring | |
Normal force due to the ring | |
None of the above |
Question 3 Explanation:
Check each option,
Option A → Incorrect, as friction would slow down the marble in some time
Option B → Incorrect, as the weight of the marble is perpendicular to the plane of the velocity
Option C → Incorrect, as the weight of the ring cannot affect the motion of the marble directly
Option D → Correct, as the normal force is always perpendicular to the velocity of the marble and is in the same plane
Option E → Incorrect, as D is correct
Option A → Incorrect, as friction would slow down the marble in some time
Option B → Incorrect, as the weight of the marble is perpendicular to the plane of the velocity
Option C → Incorrect, as the weight of the ring cannot affect the motion of the marble directly
Option D → Correct, as the normal force is always perpendicular to the velocity of the marble and is in the same plane
Option E → Incorrect, as D is correct
Question 4 |
A block of mass $2 \ kg$ is on an inclined plane. The coefficient of static friction between the block and the plane is $0.4$. How much force would be needed to set the block in motion (down the incline) if the angle of the inclined plane is $12°$?
$3.67 \ N$ | |
$7.82 \ N$ | |
$5.22 \ N$ | |
$4.15 \ N$ | |
$2.33 \ N$ |
Question 4 Explanation:
In equilibrium, the free body diagram of the block is as follows:

For equilibrium,
$N = 2g \cos 12°$ and $f_r = 2g \ \sin 12°$
Using $g = 10 \ m/s^2,$
$N = 19.56 \ N$ and $f_r = 4.15 \ N$
In static condition, $f_r ≤ μN$ (which is true for the system)
Extra force needed to set the block in motion (down the incline)
$=μN-f_r$
$=0.4 × 19.56 - 4.15$
$=7.82 - 4.15$
$=3.67 \ N$

For equilibrium,
$N = 2g \cos 12°$ and $f_r = 2g \ \sin 12°$
Using $g = 10 \ m/s^2,$
$N = 19.56 \ N$ and $f_r = 4.15 \ N$
In static condition, $f_r ≤ μN$ (which is true for the system)
Extra force needed to set the block in motion (down the incline)
$=μN-f_r$
$=0.4 × 19.56 - 4.15$
$=7.82 - 4.15$
$=3.67 \ N$
Question 5 |
Two blocks are connected by a massless string of length $l$. A force of $25 \ N$ acts on the right block, as shown below.
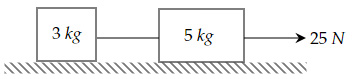
If the coefficient of friction for the right block is $0.33$, then what is the value of the coefficient of friction $μ$ for the left block? (Assume the system remains just in equilibrium and any small force can set the system in motion.)
$0.250$ | |
$0.333$ | |
$0.223$ | |
$0.252$ | |
$0.283$ |
Question 5 Explanation:
The free body diagram for the two-block system is given below:
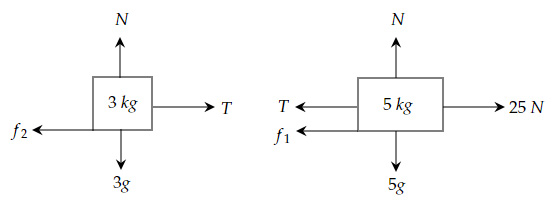
For the right block: $25 = T + f_1$ and $N = 5g =50$
Combining the two equations:
$25 = T +0.33 × 50$
$T = 8.5 \ N$
For the left block: $T = f_2$ and $N = 3g = 30$
Combining the two equations:
$8.5 = 30μ$
$μ = 0.283$

For the right block: $25 = T + f_1$ and $N = 5g =50$
Combining the two equations:
$25 = T +0.33 × 50$
$T = 8.5 \ N$
For the left block: $T = f_2$ and $N = 3g = 30$
Combining the two equations:
$8.5 = 30μ$
$μ = 0.283$
Question 6 |
Two blocks are kept on each other, as shown below.
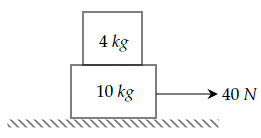
The coefficient of static friction between the two blocks is $0.25$, and the coefficient of kinetic friction is $0.18$. If a force of $40 \ N$ acts on the lower block, what will be the acceleration of the upper block? (Assume there is no friction between the lower block and the floor)
$2.25 \ m/s^2$ | |
$2.85 \ m/s^2$ | |
$1.80 \ m/s^2$ | |
$1.55 \ m/s^2$ | |
$1.20 \ m/s^2$ |
Question 6 Explanation:
Assuming the two blocks move together with the same acceleration a,
$a = \dfrac{F}{m_{down} + m_{up}}$
$=\dfrac{40}{14}$
$=2.85 \ m/s^2$
The free body diagram for the upper block is:

Thus, for the block to move with an acceleration of $2.85 \ m/s^2$ the frictional force must be at least $4 × 2.85 = 11.4 \ N$
Maximum value of static friction $= 0.25 × 40 = 10 N < 11.4 \ N$
Thus, the upper block slides with acceleration lesser than the lower block
$a = \dfrac{μ_k \ N}{m}$
$= \dfrac{0.18×40}{4} $
$= 1.8 \ m/s^2 $
$a = \dfrac{F}{m_{down} + m_{up}}$
$=\dfrac{40}{14}$
$=2.85 \ m/s^2$
The free body diagram for the upper block is:

Thus, for the block to move with an acceleration of $2.85 \ m/s^2$ the frictional force must be at least $4 × 2.85 = 11.4 \ N$
Maximum value of static friction $= 0.25 × 40 = 10 N < 11.4 \ N$
Thus, the upper block slides with acceleration lesser than the lower block
$a = \dfrac{μ_k \ N}{m}$
$= \dfrac{0.18×40}{4} $
$= 1.8 \ m/s^2 $
Question 7 |
A particle of mass $m$ is moving through a horizontally oriented medium. The particle experiences a drag force of $γv$ in a direction opposite to the velocity. If there is no other force acting on the particle, then which of the below equations represents the motion of the particle?
$m \dfrac{dv}{dt} - γv = 0$ | |
$m \dfrac{dv}{dt} + γv = 0$ | |
$m \dfrac{dv}{dt} - γv = ma$ | |
$m \dfrac{dv}{dt} + 2γv = 0$ | |
None of the above |
Question 7 Explanation:
$F = m \dfrac{dv}{dt}$
The only force acting on the particle is the drag force of the form $-γv$
Thus, $m \dfrac{dv}{dt} = -γv$
Or $m \dfrac{dv}{dt} + γv = 0$
The only force acting on the particle is the drag force of the form $-γv$
Thus, $m \dfrac{dv}{dt} = -γv$
Or $m \dfrac{dv}{dt} + γv = 0$
Question 8 |
A stone of mass $m$ tied to a massless string of length $r$ is set into motion. If the stone moves in a vertical circle, what is the minimum velocity that the stone must have when it is at the topmost point of the circle?
$\sqrt{5gr}$ | |
$\sqrt{4gr}$ | |
$\sqrt{3gr}$ | |
$\sqrt{2gr}$ | |
$\sqrt{gr}$ |
Question 8 Explanation:
For minimum velocity, Tension force $= 0 \ N$
At the topmost point, the centripetal force is provided by the gravitational force of the stone
$mg = \dfrac{mv^2}{r} → v = \sqrt{rg} $
At the topmost point, the centripetal force is provided by the gravitational force of the stone
$mg = \dfrac{mv^2}{r} → v = \sqrt{rg} $
Question 9 |
The velocity vector of a car of mass m is given by the equation:
$\overrightarrow{v}(t) = 5t \skew{2.5}\hat{i} + (10 -t^2) \skew{4}\hat{j}$
What is the average force acting on the car from $t = 1$ to $t = 4$?
$2m(\skew{2.3}\hat{i} + \skew{4.5}\hat{j} )$ | |
$5m(\skew{2.3}\hat{i} - \skew{4.5}\hat{j} )$ | |
$4m(\skew{2.3}\hat{i} - \skew{4.5}\hat{j})$ | |
$m(2\skew{2.3}\hat{i} - 3 \skew{4.5}\hat{j} )$ | |
$3m(\skew{2.3}\hat{i} - \skew{4.5}\hat{j})$ |
Question 9 Explanation:
$\overrightarrow{v}(t = 1)=5 \skew{2}\hat{i} + 9 \skew{5}\hat{j}$ and $\overrightarrow{v}(t=4)=20 \skew{2}\hat{i} -6 \skew{5}\hat{j}$
Average acceleration
$=\dfrac{\overrightarrow{v}(t=4) - \overrightarrow{v}(t=1)}{4 - 1}$
$=\dfrac{15 \skew{2}\hat{i} - 15 \skew{5}\hat{j} }{3}$
$=5 \skew{2}\hat{i}-5 \skew{5}\hat{j}$
Average force $= m × \overrightarrow{a}=5m( \skew{2}\hat{i} - \skew{5}\hat{j} )$
Average acceleration
$=\dfrac{\overrightarrow{v}(t=4) - \overrightarrow{v}(t=1)}{4 - 1}$
$=\dfrac{15 \skew{2}\hat{i} - 15 \skew{5}\hat{j} }{3}$
$=5 \skew{2}\hat{i}-5 \skew{5}\hat{j}$
Average force $= m × \overrightarrow{a}=5m( \skew{2}\hat{i} - \skew{5}\hat{j} )$
Question 10 |
Questions 10, 11 and 12 are based on the below information:
Look at the below system of three blocks.

The strings and the pulley are massless and the frictional force between the blocks and the surface is zero. When the system starts from rest, the tension force between the $4 \ kg$ block and the $2 \ kg$ block is,
$20 \ N$ | |
$12 \ N$ | |
$15 \ N$ | |
$10 \ N$ | |
$8 \ N$ |
Question 10 Explanation:
The entire system moves with the same magnitude of acceleration
For the block moving vertically: $2g - T = 2a$
For the two-block system moving horizontally: $T = 6a$
Using the two equations, $2g - 6a = 2a → a = \dfrac{g}{4}= 2.5 \ m/s^2$
For the 4 kg block, the equation of motion is:
$T_1 = 4a → T_1 = 10 \ N $
For the block moving vertically: $2g - T = 2a$
For the two-block system moving horizontally: $T = 6a$
Using the two equations, $2g - 6a = 2a → a = \dfrac{g}{4}= 2.5 \ m/s^2$
For the 4 kg block, the equation of motion is:
$T_1 = 4a → T_1 = 10 \ N $
Question 11 |
Look at the below system of three blocks.

What is the acceleration of the $2 \ kg$ block kept on the table?
$2.5 \ m/s^2$ | |
$2.0 \ m/s^2$ | |
$3.3 \ m/s^2$ | |
$4.2 \ m/s^2$ | |
$1.8 \ m/s^2$ |
Question 11 Explanation:
From question 10,
$a = \dfrac{g}{4}$
Thus, the acceleration of the system of blocks is equal to
$2.5 \ m/s^2 $
$a = \dfrac{g}{4}$
Thus, the acceleration of the system of blocks is equal to
$2.5 \ m/s^2 $
Question 12 |
Look at the below system of three blocks.

At $t=t_{break}$, the string between the $4 \ kg$ block and the $2 \ kg$ block breaks. What will be the acceleration of the $2 \ kg$ block now?
$3 \ m/s^2$ | |
$4 \ m/s^2$ | |
$5 \ m/s^2$ | |
$6 \ m/s^2$ | |
None of the above |
Question 12 Explanation:
After $t=t_{break}$,
For the block moving vertically: $2g-T=2a$
For the one-block system moving horizontally: $T=2a$
Using the two equations, $2g-2a=2a→a=\dfrac{g}{2}=5 \ m/s^2$
For the block moving vertically: $2g-T=2a$
For the one-block system moving horizontally: $T=2a$
Using the two equations, $2g-2a=2a→a=\dfrac{g}{2}=5 \ m/s^2$
Question 13 |
A block at the bottom of an inclined plane is given a sharp push at $t = 0 \ s$.

As a result, the block moves upwards and travels a distance $h$ before it starts sliding down. The coefficient of friction between the block and the inclined plane is $0.15$, and the angle of inclination is $25°$. What is the value of $h$?
$34.56 \ m$ | |
$30.60 \ m$ | |
$32.04 \ m$ | |
$29.03 \ m$ | |
$22.16 \ m$ |
Question 13 Explanation:
The free body diagram of the block is:
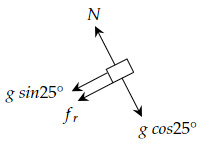
The equations of motion are:
$N=g \ \cos 25°$ and $g \ \sin 25° +f_r=a$
Using $f_r=0.15×N$ in the above equations gives,
$a=g \sin 25° +0.15g \ \cos 25° $
$a=g(\sin 25° +0.15 \ \cos 25° )$
$a=5.58 \ m/s^2$
Using $ a=5.58 \ m/s^2, u=18 \ m/s$ and $v=0 \ m/s$ in $v^2=u^2-2ah$ gives,
$h=\dfrac{u^2}{2a} = \dfrac{18^2}{2×5.58}$
$h=29.03 \ m$

The equations of motion are:
$N=g \ \cos 25°$ and $g \ \sin 25° +f_r=a$
Using $f_r=0.15×N$ in the above equations gives,
$a=g \sin 25° +0.15g \ \cos 25° $
$a=g(\sin 25° +0.15 \ \cos 25° )$
$a=5.58 \ m/s^2$
Using $ a=5.58 \ m/s^2, u=18 \ m/s$ and $v=0 \ m/s$ in $v^2=u^2-2ah$ gives,
$h=\dfrac{u^2}{2a} = \dfrac{18^2}{2×5.58}$
$h=29.03 \ m$
Question 14 |
A time-dependent centripetal force acts on an object of mass $2.4 \ kg$. The expression for the centripetal force is given as,
$\overrightarrow{f}_{cent} (t)=10[\cos 8t \skew{2.5}\hat{i} + \sin 8t \skew{4}\hat{j} ] N$
The object moves in a circle of radius 3 cm. Find the speed of the object when $t = 6 \ s$. (Note: The angles are in radians)
$0.980 \ m/s$ | |
$0.060 \ m/s$ | |
$0.802 \ m/s$ | |
$2.451 \ m/s$ | |
$0.353 \ m/s$ |
Question 14 Explanation:
$\overrightarrow{f}_{cent} (t=6)=10[\cos \ 48 \skew{2}\hat{i} + \sin \ 48 \skew{5}\hat{j} ]$
Thus, the magnitude of the centripetal force is
$\sqrt{10^2 (\sin^2 \ 48 + \cos^2 \ 48)} =10 \ N$
Since, $F = \dfrac{mv^2}{r} → v = \sqrt{ \dfrac{Fr}{m}}$
$v = \sqrt{10 × \dfrac{0.03}{2.4}}=0.353 \ m/s $
Thus, the magnitude of the centripetal force is
$\sqrt{10^2 (\sin^2 \ 48 + \cos^2 \ 48)} =10 \ N$
Since, $F = \dfrac{mv^2}{r} → v = \sqrt{ \dfrac{Fr}{m}}$
$v = \sqrt{10 × \dfrac{0.03}{2.4}}=0.353 \ m/s $
Question 15 |
The differential equation of an object moving through a viscous medium is given as:
$m \dfrac{dv}{dt} = -Av^3$
Where $A$ is a positive constant and $v(t)$ is the time-dependent velocity of the object. Find an expression for $v(t$) subject to the condition that $v(0)=1 \ m/s$.
$\left(1+\dfrac{2At}{m}\right)^{-1/2}$ | |
$\left(1+\dfrac{2At}{m}\right)^{-2}$ | |
$\left(1+\dfrac{2At}{m}\right)^{-1}$ | |
$\left(1+\dfrac{4At}{m}\right)^{1/2}$ | |
$\left(1+\dfrac{4At}{m}\right)^{2}$ |
Question 15 Explanation:
$m \dfrac{dv}{dt} = -Av^3$
Using separation of variables,
$ \dfrac{dv}{v^3} = -\dfrac{A}{m} \ dt$
Integrating both sides gives,
$\int \dfrac{dv}{v^3} =-\int \dfrac{A}{m} \ dt$
$\dfrac{v^{-2}}{-2} = - \dfrac{A}{m} t-c$ (Where $c$ is some constant)
$v^{-2} = \dfrac{2A}{m} t+c'$ (Where $c'$ is some other constant)
Using $v(t=0)=1 \ m/s$ gives,
$c'=1$
Thus, $v(t) = \left(1 + \dfrac{2At}{m}\right)^{-1/2}$
Using separation of variables,
$ \dfrac{dv}{v^3} = -\dfrac{A}{m} \ dt$
Integrating both sides gives,
$\int \dfrac{dv}{v^3} =-\int \dfrac{A}{m} \ dt$
$\dfrac{v^{-2}}{-2} = - \dfrac{A}{m} t-c$ (Where $c$ is some constant)
$v^{-2} = \dfrac{2A}{m} t+c'$ (Where $c'$ is some other constant)
Using $v(t=0)=1 \ m/s$ gives,
$c'=1$
Thus, $v(t) = \left(1 + \dfrac{2At}{m}\right)^{-1/2}$
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 15 questions to complete.
|
List |
Next Practice Test:
Unit 3: Work, Energy, & Power >>
AP Physics C Mechanics Main Menu >>
