The below test on kinematics will check the concepts of motion in one and two dimensions, including relative motion, basic vector notations, and its use in solving problems. Projectile and uniform circular motion are also included as an application of the concepts.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
John starts running from $x = 0\ m$. His speed as a function of time $t$ is given by $v(t) = \dfrac{1}{20} \ t(16-t)\ m/s$. For which of the below time instants is John’s speed a maximum?
$9 \ s$ | |
$4 \ s$ | |
$8\ s$ | |
$13 \ s$ | |
$16 \ s$ |
Question 1 Explanation:
Substitute the time instants $(t)$ in $v(t)$ for each option and compare its magnitude:
Option A $→ v(t=9) = \frac{1}{20} \times 9 \times (16 − 9) = 3.15\ m/s$
Option B $→ v(t=4)= \frac{1}{20} \times 4 \times (16-4) = 2.40\ m/s$
Option C $→ v(t=8)= \frac{1}{20} \times 8 \times (16-8) = 3.20\ m/s$
Option D $→ v(t=13)= \frac{1}{20} \times 13 \times (16-13) = 1.95\ m/s$
Option E $→ v(t=16)= \frac{1}{20} \times 16 \times (16-16) = 0.00\ m/s$
Maximum speed is when $t=8\ s$ (Option C)
Option A $→ v(t=9) = \frac{1}{20} \times 9 \times (16 − 9) = 3.15\ m/s$
Option B $→ v(t=4)= \frac{1}{20} \times 4 \times (16-4) = 2.40\ m/s$
Option C $→ v(t=8)= \frac{1}{20} \times 8 \times (16-8) = 3.20\ m/s$
Option D $→ v(t=13)= \frac{1}{20} \times 13 \times (16-13) = 1.95\ m/s$
Option E $→ v(t=16)= \frac{1}{20} \times 16 \times (16-16) = 0.00\ m/s$
Maximum speed is when $t=8\ s$ (Option C)
Question 2 |
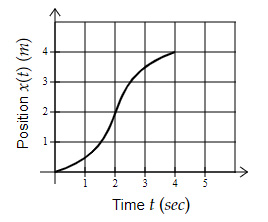
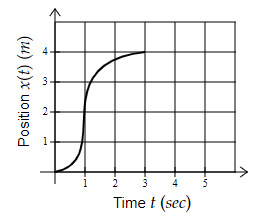
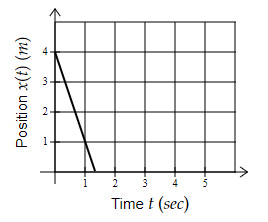
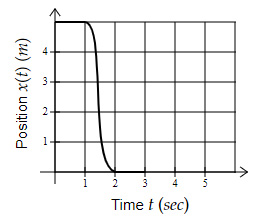
Which position-time graph (in 1D) shows an average speed of $5\ m/s$ over the time interval when the object is in motion?
 | |
 | |
 | |
 | |
 |
Question 2 Explanation:
Average Speed is equal to the magnitude of Average Velocity
And, Average Velocity $=\dfrac{r(t_2 ) - r(t_1 )}{t_2 - t_1 }$
Check each option,
Option A $→$ Average Velocity $= \frac{4 - 0}{4 - 0} = 1.00\ m/s$
Option B $→$ Average Velocity $= \dfrac{4 - 0}{3 - 0} = 1.33\ m/s$
Option C $→$ Average Velocity $= \dfrac{1 - 4}{1 - 0} = -3.00\ m/s$
Option D $→$ Average Velocity $= \dfrac{4 - 0}{2 - 0} = 2.00\ m/s$
Option E $→$ Average Velocity $= \dfrac{0 - 5}{2 - 1} = -5.00\ m/s$
Thus, option E shows an average speed of $5\ m/s$
(Speed is magnitude of velocity)
And, Average Velocity $=\dfrac{r(t_2 ) - r(t_1 )}{t_2 - t_1 }$
Check each option,
Option A $→$ Average Velocity $= \frac{4 - 0}{4 - 0} = 1.00\ m/s$
Option B $→$ Average Velocity $= \dfrac{4 - 0}{3 - 0} = 1.33\ m/s$
Option C $→$ Average Velocity $= \dfrac{1 - 4}{1 - 0} = -3.00\ m/s$
Option D $→$ Average Velocity $= \dfrac{4 - 0}{2 - 0} = 2.00\ m/s$
Option E $→$ Average Velocity $= \dfrac{0 - 5}{2 - 1} = -5.00\ m/s$
Thus, option E shows an average speed of $5\ m/s$
(Speed is magnitude of velocity)
Question 3 |
Lilly’s position vector $\overrightarrow{r}$ is a function of time $t$ given by the relation,
$\overrightarrow{r} (t)=2t \skew{2.5}\hat{i} + (5-t^2 ) \skew{4}\hat{j} \, \, m$
What is Lilly’s average velocity as she moves from $t = 2 \ s$ to $t = 4 \ s$?
$ 2 \skew{2.3}\hat{i} − 6 \skew{4.5}\hat{j} \ m/s$ | |
$2 \skew{2.3}\hat{i}+3 \skew{4.5}\hat{j} \ m/s$ | |
$4 \skew{2.3}\hat{i} −12 \skew{4.5}\hat{j} \ m/s$ | |
$6 \skew{2.3}\hat{i} +3 \skew{4.5}\hat{j} \ m/s$ | |
$10\skew{2.3} \hat{i} − 4 \skew{4.5}\hat{j} \ m/s$ |
Question 3 Explanation:
$\overrightarrow{r} (t)=2t \skew{2}\hat{i}+(5-t^2 ) \skew{5}\hat{j} $
So, $\overrightarrow{r} (t=2)=4 \skew{2}\hat{i}+ \skew{5}\hat{j} \ and \ \overrightarrow{r} (t=4)=8 \skew{2}\hat{i} -11 \skew{5}\hat{j}$
Displacement$ (\Delta \overrightarrow{r} )=\overrightarrow{r} (t=4)-\overrightarrow{r} (t=2)$
$=(8 \skew{2}\hat{i} -11 \skew{5}\hat{j} )-(4 \skew{2}\hat{i} + \skew{5}\hat{j} )$
$=4 \skew{2}\hat{i} -12 \skew{4}\hat{j}$
Time interval $(\Delta t)=4-2=2$
Average velocity $=\dfrac{1}{2} (4 \skew{2}\hat{i} -12 \skew{5}\hat{j})=2 \skew{2}\hat{i} -6 \skew{5}\hat{j}$
So, $\overrightarrow{r} (t=2)=4 \skew{2}\hat{i}+ \skew{5}\hat{j} \ and \ \overrightarrow{r} (t=4)=8 \skew{2}\hat{i} -11 \skew{5}\hat{j}$
Displacement$ (\Delta \overrightarrow{r} )=\overrightarrow{r} (t=4)-\overrightarrow{r} (t=2)$
$=(8 \skew{2}\hat{i} -11 \skew{5}\hat{j} )-(4 \skew{2}\hat{i} + \skew{5}\hat{j} )$
$=4 \skew{2}\hat{i} -12 \skew{4}\hat{j}$
Time interval $(\Delta t)=4-2=2$
Average velocity $=\dfrac{1}{2} (4 \skew{2}\hat{i} -12 \skew{5}\hat{j})=2 \skew{2}\hat{i} -6 \skew{5}\hat{j}$
Question 4 |
An object of mass $2\ kg$, starting from rest, accelerates uniformly for $5\ s$. If it covered a distance of $40\ m$ during this time interval, what distance would it cover in the same time if its acceleration was $4$ times larger than the initial acceleration?
$160 \ m$ | |
$80 \ m$ | |
$120 \ m$ | |
$100 \ m$ | |
$200 \ m$ |
Question 4 Explanation:
$s=ut+\dfrac{1}{2} \ at^2 $
For an object starting from rest, $u = 0$
$→s∝a$
Thus, when $a'=4a$ then $s'= 4s = 4 × 40 = 160\ m$
For an object starting from rest, $u = 0$
$→s∝a$
Thus, when $a'=4a$ then $s'= 4s = 4 × 40 = 160\ m$
Question 5 |
The graph of the velocity $v$, as a function of time $t$, is shown below.

Which option would show the correct relation for the acceleration $a(t)$?
(Hint: The graph is a parabola of the form $y = b(x-a)^2$)
$a(t) = \dfrac{4}{3} t$ | |
$a(t) = \dfrac{2}{3} (t-3)^2$ | |
$a(t) = \dfrac{4}{3} (t-3)$ | |
$a(t) = \dfrac{2}{3} t^2$ | |
$a(t) = \dfrac{4}{3} t- \dfrac{2}{3}$ |
Question 5 Explanation:
Using the hint: $v(t)=\dfrac{2}{3} (t-3)^2$
Since, $a(t) = \dfrac{dv}{dt}$
$a(t) =\dfrac{2}{3} \dfrac{d}{dt} (t-3)^2$
$ = \dfrac{2}{3} \ 2(t-3) $
$ = \dfrac{4}{3} (t-3) $
Since, $a(t) = \dfrac{dv}{dt}$
$a(t) =\dfrac{2}{3} \dfrac{d}{dt} (t-3)^2$
$ = \dfrac{2}{3} \ 2(t-3) $
$ = \dfrac{4}{3} (t-3) $
Question 6 |
A projectile is launched at an angle of $20°$ with a speed of $10\ m/s$. Another projectile is launched at an angle of $40°$ with the same speed. The difference between the range of the two projectiles is,
(Use $g=10\ m/s^2$)
$8.62\ m$ | |
$25.4\ m$ | |
$34.0\ m$ | |
$3.42\ m$ | |
$10.0\ m$ |
Question 6 Explanation:
Range $=\dfrac{v_o^2}{g} \ \sin2θ$
For $θ = 20°$, Range $= 10 \sin 40°$
For $θ = 40°$, Range $= 10 \sin 80°$
Difference $= 10 \ (sin 80°-\sin40° )$
$= 10 \ (0.342) $
$= 3.42\ m $
For $θ = 20°$, Range $= 10 \sin 40°$
For $θ = 40°$, Range $= 10 \sin 80°$
Difference $= 10 \ (sin 80°-\sin40° )$
$= 10 \ (0.342) $
$= 3.42\ m $
Question 7 |
The velocity of particle $A$ is given by $\overrightarrow{v}_A (t)=(t-2) \skew{2.5}\hat{i} +5 \skew{4}\hat{j},$ and the velocity of particle $B$ is given by $\overrightarrow{v}_B (t)=6 \skew{2.5}\hat{i} + (4-t) \skew{4}\hat{j}.$ The velocity of $B$, as seen by $A$, is given by,
$\overrightarrow{v}_{BA} (t) = (8-t) \skew{2.3}\hat{i} -(t+1) \skew{4.5}\hat{j}$ | |
$\overrightarrow{v}_{BA} (t) = (4-t) \skew{2.3}\hat{i} +(t+1) \skew{4.5}\hat{j}$ | |
$\overrightarrow{v}_{BA} (t) = (8+t) \skew{2.3}\hat{i} -(t+1) \skew{4.5}\hat{j}$ | |
$\overrightarrow{v}_{BA} (t) = (8-t) \skew{2.3}\hat{i} +(t+3) \skew{4.5}\hat{j}$ | |
$\overrightarrow{v}_{BA} (t) = (t-8) \skew{2.3}\hat{i} -(t+1) \skew{4.5}\hat{j}$ |
Question 7 Explanation:
$\overrightarrow{v}_{BA} (t)=\overrightarrow{v}_{B} $(t)-$\overrightarrow{v}_A (t) $
$= 6 \skew{2}\hat{i}+(4-t) \skew{5}\hat{j} -(t-2) \skew{2}\hat{i} -5 \skew{5}\hat{j} $
$= (8-t) \skew{2}\hat{i} -(1+t) \skew{5}\hat{j} $
$= 6 \skew{2}\hat{i}+(4-t) \skew{5}\hat{j} -(t-2) \skew{2}\hat{i} -5 \skew{5}\hat{j} $
$= (8-t) \skew{2}\hat{i} -(1+t) \skew{5}\hat{j} $
Question 8 |
Which of the below statements is TRUE for the position-time graphs of two particles, $A$ and $B$?
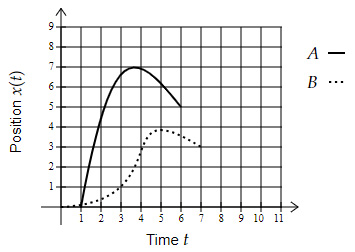
The average velocity of $A$ is less than $B$ | |
The acceleration of $A$ is always $0$ | |
The instantaneous velocity of $B$ at $t = 3\ s$ is more than $5\ m/s$ | |
The velocity of $A$ and $B$ becomes zero once during their journey | |
The acceleration of $B$ never becomes negative |
Question 8 Explanation:
Check each option,
Option A $→$ False, because displacement of $A$ is more than $B$ and the time interval of $A$ is less than $B$
Option B $→$ False, because velocity of $A$ keeps changing
Option C $→$ False, because velocity of $B$ at $t=3 \ s$ is about $\dfrac{2-0}{4-2}=1 \ m/s$
Option D $→$ True, because velocity of $A$ is $0 \ m/s$ in the interval $(3,4)$ while $B$ is $0 \ m/s$ in the interval $(4,6)$
Option E $→$ False, because velocity of $B$ decreases after $t=4 \ s$
Option A $→$ False, because displacement of $A$ is more than $B$ and the time interval of $A$ is less than $B$
Option B $→$ False, because velocity of $A$ keeps changing
Option C $→$ False, because velocity of $B$ at $t=3 \ s$ is about $\dfrac{2-0}{4-2}=1 \ m/s$
Option D $→$ True, because velocity of $A$ is $0 \ m/s$ in the interval $(3,4)$ while $B$ is $0 \ m/s$ in the interval $(4,6)$
Option E $→$ False, because velocity of $B$ decreases after $t=4 \ s$
Question 9 |
The velocity $v(t)$ of a particle when passing through a medium is given by the formula,
$v(t) = \dfrac{mg}{γ} (1-e^{\dfrac{-γt}{m}} )$
Where $g$ is the acceleration due to gravity, $γ$ is a constant, $m$ is the mass of the particle, and $t$ is the time. What is the maximum velocity that the particle will reach when passing through the medium?
$\dfrac{2mg}{γ}$ | |
$\dfrac{mg}{γ}$ | |
$\dfrac{mg}{2}γ$ | |
$\dfrac{mg}{3γ}$ | |
$\dfrac{mg}{4γ}$ |
Question 9 Explanation:
For maximum velocity, $e^{\dfrac{-γt}{m}}$ should be as small as possible
Which is true when $t$ is large enough
For large $t, v(t) = \dfrac{mg}{γ} (1-0) = \dfrac{mg}{γ}$
Which is true when $t$ is large enough
For large $t, v(t) = \dfrac{mg}{γ} (1-0) = \dfrac{mg}{γ}$
Question 10 |
A particle moving in 1D has velocity $v(t) = 6t + 3t^2 \ m/s$. What is the magnitude of displacement $\Delta r$ of the particle as it moves from $t = 1 \ s$ to $t=4 \ s$?
$92 \ m$ | |
$85 \ m$ | |
$120 \ m$ | |
$72 \ m$ | |
$108 \ m$ |
Question 10 Explanation:
$\Delta r=\int_1^4 v(t) \ dt $
$=\int_1^4 (6t+3t^2 ) \ dt$
$=3t^2+t^3 |_1^4$
$=3(16-1)+(64-1)$
$=45+63$
$=108 \ m$
$=\int_1^4 (6t+3t^2 ) \ dt$
$=3t^2+t^3 |_1^4$
$=3(16-1)+(64-1)$
$=45+63$
$=108 \ m$
Question 11 |
Questions 11 and 12 are based on the below information:
A projectile is launched, as shown in the diagram below.
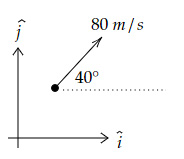
What will be the velocity of the projectile after $t = 2 \ s$?
(Use $g = 10 \ m/s^2 $)
$-61.3 \skew{2.3}\hat{i}+51.4 \skew{4.5}\hat{j} \ m/s$ | |
$61.3 \skew{2.3}\hat{i} +51.4 \skew{4.5}\hat{j} \ m/s$ | |
$-63.1 \skew{2.3}\hat{i} +31.4 \skew{4.5}\hat{j} \ m/s$ | |
$63.1 \skew{2.3}\hat{i} +31.4 \skew{4.5}\hat{j} \ m/s$ | |
$61.3 \skew{2.3}\hat{i} +31.4 \skew{4.5}\hat{j} \ m/s$ |
Question 11 Explanation:
The horizontal $(x)$ component of the velocity is unchanged and is given by,
$v_x = 80 \cos 40° = 61.3 \ m/s $
The vertical $(y)$ component of the velocity changes as,
$v_y = v_{yo}-gt$
Where $v_{yo} = 80 \sin 40° = 51.4 \ m/s$
$v_y = 51.4-10×2 = 31.4 \ m/s$
Thus, the velocity vector is equal to,
$61.3 \skew{2}\hat{i}+31.4 \skew{5}\hat{j} \ m/s $
$v_x = 80 \cos 40° = 61.3 \ m/s $
The vertical $(y)$ component of the velocity changes as,
$v_y = v_{yo}-gt$
Where $v_{yo} = 80 \sin 40° = 51.4 \ m/s$
$v_y = 51.4-10×2 = 31.4 \ m/s$
Thus, the velocity vector is equal to,
$61.3 \skew{2}\hat{i}+31.4 \skew{5}\hat{j} \ m/s $
Question 12 |
A projectile is launched, as shown in the diagram below.

What is the displacement of the projectile after $t = 4 \ s$?
$252.0 \skew{2.3}\hat{i} +120.2 \skew{4.5}\hat{j} \ m$ | |
$265.3 \skew{2.3}\hat{i} +133.9 \skew{4.5}\hat{j} \ m$ | |
$245.2 \skew{2.3}\hat{i} +125.6 \skew{4.5}\hat{j} \ m$ | |
$245.5 \skew{2.3}\hat{i} +114.4 \skew{4.5}\hat{j} \ m$ | |
$230.4 \skew{2.3}\hat{i} +125.6 \skew{4.5}\hat{j} \ m$ |
Question 12 Explanation:
$\Delta r_x=v_x×\Delta t $
$→\Delta r_x=61.3×4=245.2 \ m$
$\Delta r_y=v_{yo} \Delta t- \dfrac{1}{2} g\Delta t^2$
$→\Delta r_y=51.4×4-\dfrac{1}{2}×10×4^2=125.6 \ m$
Thus, the displacement vector is equal to,
$245.2 \skew{2}\hat{i} +125.6 \skew{5}\hat{j} \ m$
$→\Delta r_x=61.3×4=245.2 \ m$
$\Delta r_y=v_{yo} \Delta t- \dfrac{1}{2} g\Delta t^2$
$→\Delta r_y=51.4×4-\dfrac{1}{2}×10×4^2=125.6 \ m$
Thus, the displacement vector is equal to,
$245.2 \skew{2}\hat{i} +125.6 \skew{5}\hat{j} \ m$
Question 13 |
A block starts decelerating at $3 \ m/s^2$ from time $ t = 0 \ s$, and covers $30 \ m$ before it stops. Which option is the closest to the average speed of the block?
$12.80 \ m/s$ | |
$13.41 \ m/s$ | |
$8.90 \ m/s$ | |
$6.70 \ m/s$ | |
$11.05 \ m/s$ |
Question 13 Explanation:
Using $a=-3 m/s^2, s=30 m, v=0 m/s $ in the equation
$v^2= u^2+2as$ gives,
$0 = u^2-2×3×30$
$u^2 = 180→u=3 \sqrt{20} \ m/s$
$t = \dfrac{v - u}{a}$
$= \dfrac{0 - 3 \sqrt{20}}{- 3}$
$= \sqrt{20} \ s$
Average speed $ = \dfrac{Distance}{Time}$
$= \dfrac{30}{ \sqrt{20}}$
$= 6.70 m/s$
$v^2= u^2+2as$ gives,
$0 = u^2-2×3×30$
$u^2 = 180→u=3 \sqrt{20} \ m/s$
$t = \dfrac{v - u}{a}$
$= \dfrac{0 - 3 \sqrt{20}}{- 3}$
$= \sqrt{20} \ s$
Average speed $ = \dfrac{Distance}{Time}$
$= \dfrac{30}{ \sqrt{20}}$
$= 6.70 m/s$
Question 14 |
An object is released from rest inside a medium, as shown below.
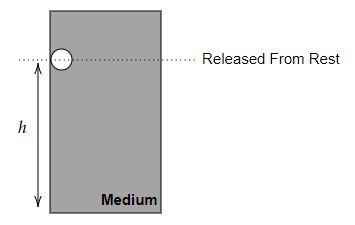
It experiences a downward acceleration $a(t) = 6at$ while moving through the medium, where $a$ is a constant. Find the time interval $\Delta t$ required for the object to fall through height $h$ in the medium.
$\left(\dfrac{2h}{a}\right)^{1/3}$ | |
$\left(\dfrac{h}{a}\right)^{2/3}$ | |
$\left(\dfrac{a}{h}\right)^{1/3}$ | |
$\left(\dfrac{a}{h}\right)^{3/2}$ | |
$\left(\dfrac{h}{a}\right)^{1/3}$ |
Question 14 Explanation:
$v(t)-v(0)= ∫_0^t 6at' \ dt' = 3at^2$
Since, $v(0)=0→v(t)=3at^2$
$r(\Delta t)-r(0)=\int_0^{\Delta t} 3at^2 \ dt=a(\Delta t)^3 $
Since, $r(0)=0 \ and \ r(\Delta t)=h →h=a\Delta t^3$
Inverting the relation gives,
$\Delta t= \left(\dfrac{h}{a}\right)^{1/3}$
Since, $v(0)=0→v(t)=3at^2$
$r(\Delta t)-r(0)=\int_0^{\Delta t} 3at^2 \ dt=a(\Delta t)^3 $
Since, $r(0)=0 \ and \ r(\Delta t)=h →h=a\Delta t^3$
Inverting the relation gives,
$\Delta t= \left(\dfrac{h}{a}\right)^{1/3}$
Question 15 |
Two boats, $I$ and $II$, are moving in a river as follows:
$I: \overrightarrow{r}(t)=8t \skew{2.5}\hat{i} +(7-2t) \skew{4}\hat{j} $
$II: \overrightarrow{r}(t)=4t^2 \skew{2.5}\hat{i} +2(t-t^2 ) \skew{4}\hat{j} $
Find the time instant $t$ when the two boats are traveling with the same velocity.
$t = 2$ | |
$t = 1$ | |
$t = 0.5$ | |
$t = 3.2$ | |
$t = 0$ |
Question 15 Explanation:
For $I$: velocity $\overrightarrow{v}=8 \skew{2}\hat{i} -2 \skew{5}\hat{j} $
For $II$: velocity $\overrightarrow{v}=8t \skew{2}\hat{i} +2(1-2t) \skew{5}\hat{j} $
For equal velocities, $8t=8→t=1$
[Also, $2(1-2t)=-2→t=1$]
Which confirms that time at which the velocities of the two boats are equal is $t=1$
For $II$: velocity $\overrightarrow{v}=8t \skew{2}\hat{i} +2(1-2t) \skew{5}\hat{j} $
For equal velocities, $8t=8→t=1$
[Also, $2(1-2t)=-2→t=1$]
Which confirms that time at which the velocities of the two boats are equal is $t=1$
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 15 questions to complete.
|
List |
Next Practice Test:
Unit 2: Newton’s Laws of Motion >>
AP Physics C Mechanics Main Menu >>
