Try our AP Stats unit 5 test. These questions focus on sampling distributions, which are the distributions of a sample statistic (usually the sample mean or sample proportion), as well as distributions and probabilities relating to a single sample, usually using the Z-table. The Central Limit Theorem as well as some guidelines about using the Normal Approximation also appear.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
For which of the following situations would this question be an appropriate question: “Does the amount of homework correlate to students’ scores?”
Students are chosen at random from a 3rd grade class and a 10th grade class, and data is collected on the amount of homework assigned and the scores they receive. | |
Students are chosen from the same 3rd grade class and data is collected on the scores they receive. | |
Students are chosen from a 3rd grade class in one school and a 3rd grade class in another school, and data is collected on the amount of homework assigned and the scores they receive. | |
In one school, 3rd grade students are randomly assigned to one of several classes with varying amounts of homework. Data is then collected on the scores the students receive. |
Question 1 Explanation:
The correct answer is (D). When asking questions about different samples, the samples need to be taken from the same population. Two different grade levels are not considered the same population for this topic, because there are other factors that change from 3rd to 10th grade. Collecting score data from a single class, while it would be the same population, wouldn’t provide comparison. Students from different schools are not necessarily the same population, as there could be other factors besides homework assigned. The closest way to have different sample data within the same population is to have students from the same school randomly assigned to classes within that school.
Question 2 |
A potter is working on creating clay pots. The mean height of the pots thrown is 10 inches with a standard deviation of 1.5 inches. What is the probability that a randomly selected pot is between 10.5 and 10.75 inches?
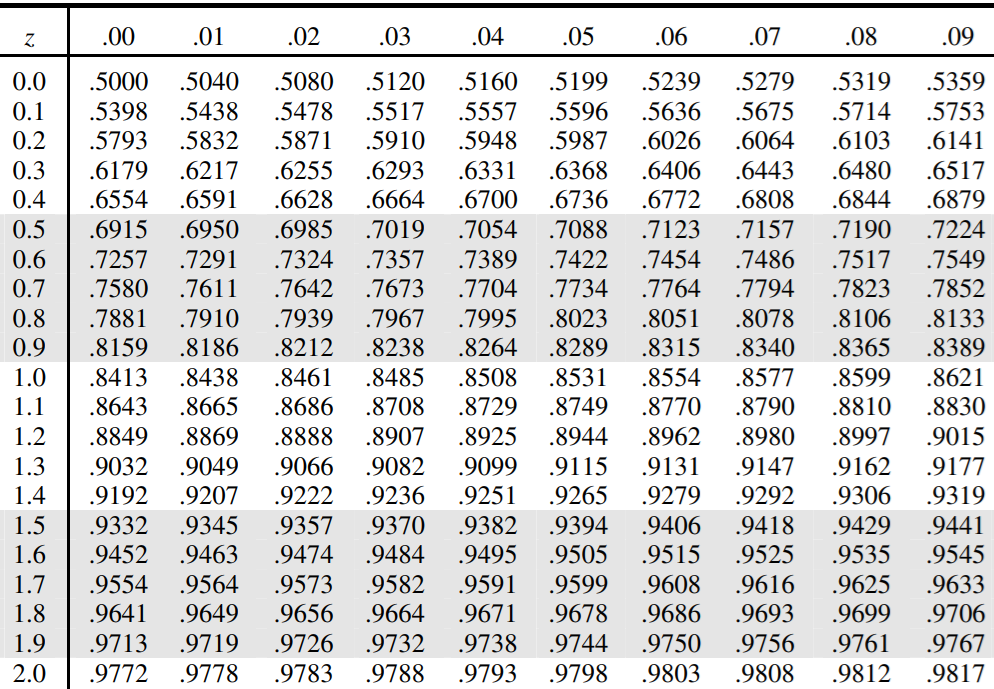
6.22% | |
9.87% | |
12.93% | |
10.15% |
Question 2 Explanation:
The correct answer is (A). The Z-table shows the probability that the random variable will be less than or equal to a certain amount of standard deviations away from the mean.
10.5 is approximately $\frac{(10.5 − 10)}{1.5}$ = +0.33 standard deviations from the mean, corresponding to 0.6293.
10.75 is $\frac{(10.75 − 10)}{1.5}$ = +0.5 standard deviations from the mean, corresponding to 0.6915.
P(pot is between 10.5 and 10.75 in) = P(pot is below 10.75 in) − P(pot is below 10.5 in)
0.6915 − 0.6293 = 0.0622 or 6.22%
10.5 is approximately $\frac{(10.5 − 10)}{1.5}$ = +0.33 standard deviations from the mean, corresponding to 0.6293.
10.75 is $\frac{(10.75 − 10)}{1.5}$ = +0.5 standard deviations from the mean, corresponding to 0.6915.
P(pot is between 10.5 and 10.75 in) = P(pot is below 10.75 in) − P(pot is below 10.5 in)
0.6915 − 0.6293 = 0.0622 or 6.22%
Question 3 |
The finishing times for a track race had an mean of 26.3 seconds with a standard deviation of 0.25 seconds. Between what two values will the middle 33% of the data fall?

25.9667 to 26.6333 | |
26.1926 to 26.4075 | |
26.2175 to 26.3825 | |
26.2013 to 26.3987 |
Question 3 Explanation:
The correct answer is (B). The middle 33% of data will have approximately 16.6% of data on each side of the mean. The probability we’re looking for is therefore 0.5 + .1666 = .6666. This corresponds most closely with 0.43 standard deviations from the mean. With a standard deviation of 0.25 seconds, 0.25﹡0.43 = 0.1075. Adding this number to 26.3 and subtracting this number from 26.3 gives us the interval 26.1926 to 26.4075.
Question 4 |
You conduct a survey to find out what proportion of people in your town eat bagels. You stand outside the bakery and ask passers-by if they eat bagels. Which of the following are true?
-
Your results contain no bias since you are not specifically asking people in the bakery; some of the people are passing by and not going in.
-
The results could be biased because a higher proportion of people in that area are going to the bakery.
-
Your results contain no bias as long as you pick a random day.
-
It would have been better to take the phone numbers of all the passers-by and select from them randomly and call them.
I | |
IV | |
II | |
II and IV |
Question 4 Explanation:
The correct answer is (C) . More of the people around the bakery are likely to be baked goods enthusiasts. Taking their phone numbers and selecting randomly wouldn’t help because you would be selecting from a population which itself was selected in a biased manner.
Question 5 |
A random sample of 100 high school students is taken from the population of students in a given state, for which the overall proportion of students with a driver’s license is 0.45. There is a 68% chance that the sample proportion falls between what two values?
0.14 and 0.76 | |
0.35 and 0.55 | |
0.35 and 0.45 | |
0.40 and 0.50 |
Question 5 Explanation:
The correct answer is (D). The mean is 0.45 and the standard deviation is:
$\sqrt {\frac{0.45(1 − 0.45)}{100}}≈0.05$
$np = 100(0.45) = 45$
and
$n(1-p) = 100(1-0.45) = 55$
Both are greater than 10. The Standard Deviation rule tells us that 68% of the data will fall within 1 standard deviation of the mean, or 0.45 + 0.5 and 0.45 - 0.5, which gives us an interval of 0.4 and 0.5.
$\sqrt {\frac{0.45(1 − 0.45)}{100}}≈0.05$
$np = 100(0.45) = 45$
and
$n(1-p) = 100(1-0.45) = 55$
Both are greater than 10. The Standard Deviation rule tells us that 68% of the data will fall within 1 standard deviation of the mean, or 0.45 + 0.5 and 0.45 - 0.5, which gives us an interval of 0.4 and 0.5.
Question 6 |
A video game company is looking at data regarding how many people play its flagship game, and comparing that data between two countries. In country A, 60% of people play the game; in country B, 52% of people play. The survey will ask 400 people, 200 chosen at random from each country, whether or not they play the game.
What are the mean and standard deviation of the difference between the proportions of people who play the game in each sample?
Mean = 0.08, standard deviation = 0.004 | |
Mean = 0.08, standard deviation = 0.049 | |
Mean = 0.56, standard deviation = 0.004 | |
Mean = 0.56, standard deviation = 0.049 |
Question 6 Explanation:
The correct answer is (B). The mean is the difference of the population proportions:
$(0.60-0.52 = 0.08)$
The standard deviation is:
$\sqrt {\frac {0.6(1-0.6)}{200} + \frac {0.52(1-0.52)}{200}}$
$=\sqrt {\frac {0.24}{200} + \frac{0.2496}{200}}$
$= \sqrt{0.0012+0.001248} $ $ ≈ 0.049$
$(0.60-0.52 = 0.08)$
The standard deviation is:
$\sqrt {\frac {0.6(1-0.6)}{200} + \frac {0.52(1-0.52)}{200}}$
$=\sqrt {\frac {0.24}{200} + \frac{0.2496}{200}}$
$= \sqrt{0.0012+0.001248} $ $ ≈ 0.049$
Question 7 |
For a given population of students, foot length is normally distributed with a mean of 8 inches and a standard deviation of 0.25 inches. A researcher is taking samples of 40 students. What are the mean and standard deviation of the sample mean?
Mean 8, standard deviation 0.00625 | |
Mean 8, standard deviation 0.0395 | |
Mean 8, standard deviation 0.25 | |
Mean 8, standard deviation 0.05 |
Question 7 Explanation:
The correct answer is (B). The mean will be the same as the population sample, 8. The standard deviation will be:
$\dfrac{0.25}{\sqrt{40}}≈0.0395$
$\dfrac{0.25}{\sqrt{40}}≈0.0395$
Question 8 |
A new species has been discovered and researchers are comparing two separate populations on different continents. The height of population A is 20 inches with a standard deviation of 0.8 inches. The height of population B is 22 inches with a standard deviation of 1.2 inches.
What are the mean and standard deviation for the difference in sample means with samples of size 100?
Mean = 2, deviation = 0.0208 | |
Mean = 2, deviation = 0.144 | |
Mean = 2, deviation = 0.456 | |
Mean = 2, deviation = 1.0 |
Question 8 Explanation:
The correct answer is (B). The mean is:
$22-20 = 2$
The standard deviation is:
$\sqrt {\frac{0.8^2}{100} + \frac{1.2^2}{100}}$
$= \sqrt{0.0064+0.0144} $ $ ≈ 0.144$
$22-20 = 2$
The standard deviation is:
$\sqrt {\frac{0.8^2}{100} + \frac{1.2^2}{100}}$
$= \sqrt{0.0064+0.0144} $ $ ≈ 0.144$
Question 9 |
Which of the following statements are true about the Central Limit Theorem?
-
It requires the samples to be independent of each other.
-
It requires the samples to be taken without replacement.
-
When the sample size is sufficiently large, a sampling distribution of the mean of a random variable will be distributed in the same way as the population.
-
The sampling distribution of a statistic can be simulated by generating repeated random samples from a population.
I and IV | |
I and II | |
III and IV | |
I, III, and IV |
Question 9 Explanation:
The correct answer is (A). The Central Limit Theorem states that when the sample size is sufficiently large, a sampling distribution of the mean of a random variable will be approximately normally distributed. It requires independent samples and can be simulated by generating repeated random samples from a population.
Question 10 |
Data is collected on a sample of 20 students with a population proportion of 0.4 student-athletes. Can the sampling distribution be described as approximately normal?
No, because $np$ is too small. | |
No, because $n(1-p)$ is too small. | |
No, because $np$ and $n(1-p)$ are too small. | |
Yes, because $np$ and $n(1-p)$ are large enough. |
Question 10 Explanation:
The correct answer is (A)> In this sample:
$np = 20*0.4 = 5$
and
$n(1-p) = 20 * 0.6 = 12$
Because $np$ <10, the value is too small to say the data is approximately normal.
$np = 20*0.4 = 5$
and
$n(1-p) = 20 * 0.6 = 12$
Because $np$ <10, the value is too small to say the data is approximately normal.
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 10 questions to complete.
|
List |
Next Practice Test:
Categorical Data: Proportions >>
AP Statistics Main Menu >>
