Our AP Precalculus test on exponential and logarithmic functions includes topics like the form of exponential and logarithmic functions, their properties, graphs, and regressions using exponential functions. Also, the relation between logarithmic and exponential functions as inverses of each other and arithmetic and geometric progressions are included.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
The population of bacteria in an experimental setup triples every 6 years. If the initial population of bacteria is equal to 200, what would be its population after $t$ years?
$400(3)^{t/6}$ | |
$200(1.2)^{3t}$ | |
$200(3)^{6t}$ | |
$200(3)^{t/6}$ |
Question 1 Explanation:
The correct answer is (D). The population of bacteria triples every 6 years.
If $t$ represents the number of years and $p(t)$ represents the population then,
$p(t)=200(3)^{t/6}$
If $t$ represents the number of years and $p(t)$ represents the population then,
$p(t)=200(3)^{t/6}$
Question 2 |
Which of the exponential functions below are identical?
$A: 3^{6x-2}$
$B: \dfrac{3^{6x}}{9}$
$C: \dfrac{729^x}{3}$
$A$ and $C$ | |
$B$ and $C$ | |
$A,B$ and $C$ | |
$A$ and $B$ |
Question 2 Explanation:
The correct answer is (D).
Function $A→ 3^{6x−2}=3^{−2} \cdot \ 3^{6x}= $ $ \dfrac{1}{9} 3^{6x}$
Function $B→ \dfrac{3^{6x}}{9}=\dfrac{1}{9} 3^{6x}$
Function $C→ \dfrac{729^x}{3} $ $ =\dfrac{1}{3} (3^6 )^x=\dfrac{1}{3} 3^{6x}$
Thus, functions $A$ and $B$ are equal to each other.
Function $A→ 3^{6x−2}=3^{−2} \cdot \ 3^{6x}= $ $ \dfrac{1}{9} 3^{6x}$
Function $B→ \dfrac{3^{6x}}{9}=\dfrac{1}{9} 3^{6x}$
Function $C→ \dfrac{729^x}{3} $ $ =\dfrac{1}{3} (3^6 )^x=\dfrac{1}{3} 3^{6x}$
Thus, functions $A$ and $B$ are equal to each other.
Question 3 |
What is the $y$-intercept and the range of the exponential function below?
$g(x)=2.5^{x+2}-10$
$y\text{-intercept} =- 3.75$ $\text{and range} =(-10,∞)$ | |
$y\text{-intercept} =-10$ $\text{and range} =(-10,∞)$ | |
$y\text{-intercept} =6.25$ $\text{and range} =(0,∞)$ | |
$y\text{-intercept} =- 3.75$ $\text{and range} =(-3.75,∞)$ |
Question 3 Explanation:
The correct answer is (A).
$g(x)=2.5^{x+2}-10$
$\lim\limits_{x→+∞} g(x) $ $ = \lim\limits_{x→+∞} (2.5^{x+2} - 10) $ $ =∞$
And,
$\lim\limits_{x→−∞} g(x) $ $ = \lim\limits_{x→−∞} (2.5^{x+2} - 10) $ $ =0-10=-10$
Range $=(-10,∞)$
$y$-intercept $=g(0)=2.5^{0+2}-10 $ $ =6.25-10=-3.75$
$g(x)=2.5^{x+2}-10$
$\lim\limits_{x→+∞} g(x) $ $ = \lim\limits_{x→+∞} (2.5^{x+2} - 10) $ $ =∞$
And,
$\lim\limits_{x→−∞} g(x) $ $ = \lim\limits_{x→−∞} (2.5^{x+2} - 10) $ $ =0-10=-10$
Range $=(-10,∞)$
$y$-intercept $=g(0)=2.5^{0+2}-10 $ $ =6.25-10=-3.75$
Question 4 |
If $\log_{10}A=5$ and $\log_{10}B=3$, then what is the value of
$\log_{10}\sqrt{AB^3} \,$?
$7$ | |
$6$ | |
$2$ | |
$10$ |
Question 4 Explanation:
The correct answer is (A).
$\log_{10}\sqrt{AB^3}$
$=\dfrac{1}{2} \log_{10} \ AB^3$
$=\dfrac{1}{2} \log_{10} \ A+\dfrac{3}{2} \log_{10} \ B$
$=\dfrac{1}{2}.5+\dfrac{3}{2}.3$
$=7$
$\log_{10}\sqrt{AB^3}$
$=\dfrac{1}{2} \log_{10} \ AB^3$
$=\dfrac{1}{2} \log_{10} \ A+\dfrac{3}{2} \log_{10} \ B$
$=\dfrac{1}{2}.5+\dfrac{3}{2}.3$
$=7$
Question 5 |
If $\log_4(x^2+4)=1.5$, then what is the value of $x$?
$-1,1$ | |
$-3,3$ | |
$-2,2$ | |
$-4,4$ |
Question 5 Explanation:
The correct answer is (C).
$\log_4(x^2+4)=1.5$
$4^{1.5}=x^2+4$
$x^2+4=8$
$x=±2$
$\log_4(x^2+4)=1.5$
$4^{1.5}=x^2+4$
$x^2+4=8$
$x=±2$
Question 6 |
The per-square-foot rate of houses in a metro city increases by 10% every 6 months. The per-square-foot rate is \$100 in January 2020. What is the cost of a house of area 450 sq. ft in June 2021?
You may use a calculator.
$\$57{,}825$ | |
$\$55{,}395$ | |
$\$59{,}895$ | |
$\$52{,}310$ |
Question 6 Explanation:
The correct answer is (C). Increase in the per square foot cost is 10% every 6 months.
If $t$ represents the number of months and $R(t)$ represents the rate then:
$R(t)=100(1+\frac{10}{100})^{t/6} $ $ =100(1.1)^{t/6}$
Number of months from January 2020 to June 2021 = 18.
$R(18)=100(1.1)^{18/6}=133.1$
Thus, the cost of house of area
$450 \; sq.ft=133.1×450 $ $ =\$59{,}895$
If $t$ represents the number of months and $R(t)$ represents the rate then:
$R(t)=100(1+\frac{10}{100})^{t/6} $ $ =100(1.1)^{t/6}$
Number of months from January 2020 to June 2021 = 18.
$R(18)=100(1.1)^{18/6}=133.1$
Thus, the cost of house of area
$450 \; sq.ft=133.1×450 $ $ =\$59{,}895$
Question 7 |
Which option represents the function for the graph below?
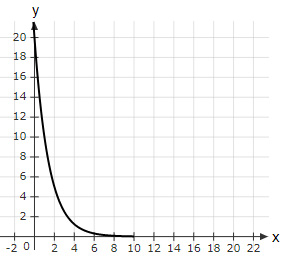
$y(x)=20(2)^{-3x}$ | |
$y(x)=5(2)^{-(x-2)}$ | |
$y(x)=5(2)^{-x}$ | |
$y(x)=0.8(5)^{-(x-2)}$ |
Question 7 Explanation:
The correct answer is (B).
Option (A) $→y(x=2)=\dfrac{20}{64}≠5$ (Incorrect function)
Option (B) $→y(x=0)=20 \,$ and $\, y(x=2)=5$ (Correct function)
Option (C) $→y(x=0)=5≠20$ (Incorrect function)
Option (D) $→y(x=2)=0.8≠5$ (Incorrect function)
Option (A) $→y(x=2)=\dfrac{20}{64}≠5$ (Incorrect function)
Option (B) $→y(x=0)=20 \,$ and $\, y(x=2)=5$ (Correct function)
Option (C) $→y(x=0)=5≠20$ (Incorrect function)
Option (D) $→y(x=2)=0.8≠5$ (Incorrect function)
Question 8 |
Work out the exponential fit for the data given below and thus find the value of $Y$ when $X=6$.
$X$ |
$0$ |
$1$ |
$2.2$ |
$3.5$ |
$4.6$ |
$5$ |
$Y$ |
$5.9$ |
$12.9$ |
$45.1$ |
$166.6$ |
$495.4$ |
$744.0$ |
You may use a calculator.
$2000.2$ | |
$2032.6$ | |
$1939.0$ | |
$1862.4$ |
Question 8 Explanation:
The correct answer is (C). Input the $X$ values as List1(L1) and $Y$ values as List2(L2)
Use the Exponential Regression module on calculator to find the equation,
$Y=5.352(2.670)^X$
$\text{For } X=6$,
$Y=5.352(2.670)^6=1939.0$
Use the Exponential Regression module on calculator to find the equation,
$Y=5.352(2.670)^X$
$\text{For } X=6$,
$Y=5.352(2.670)^6=1939.0$
Question 9 |
A purely exponentially decaying graph is translated by $4$ units horizontally to the right and $2$ units vertically downwards.
Which graph represents the function after the transformation?
 | |
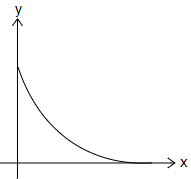 | |
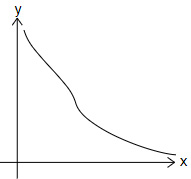 | |
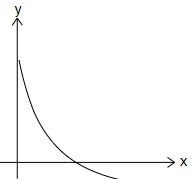 |
Question 9 Explanation:
The correct answer is (D).
Option (A) → Horizontal asymptote should be $y=-2$ (Incorrect graph)
Option (B) → Horizontal asymptote should be $y=-2$ (Incorrect graph)
Option (C) → The graph does not represent a decay graph (Incorrect graph)
Option (D) → Best representation of the graph (Correct graph)
Option (A) → Horizontal asymptote should be $y=-2$ (Incorrect graph)
Option (B) → Horizontal asymptote should be $y=-2$ (Incorrect graph)
Option (C) → The graph does not represent a decay graph (Incorrect graph)
Option (D) → Best representation of the graph (Correct graph)
Question 10 |
Find the value of $\dfrac{\log_{10}\ 0.001}{\log_{2}\ 0.25}$.
$3$ | |
$1.5$ | |
$2.5$ | |
$1$ |
Question 10 Explanation:
The correct answer is (B).
$\dfrac{\log_{10}\ 0.001}{\log_{2}\ 0.25}$
$=\dfrac{\log_{10}\ 10^{-3}}{\log_{2}\ 2^{-2}}$
$=\dfrac{-3}{-2}$
$=1.5$
$\dfrac{\log_{10}\ 0.001}{\log_{2}\ 0.25}$
$=\dfrac{\log_{10}\ 10^{-3}}{\log_{2}\ 2^{-2}}$
$=\dfrac{-3}{-2}$
$=1.5$
Question 11 |
Two functions, $h(x)$ and $f(x)$, are defined as $\log_{e}x$ and $x(x+e)$, respectively. What is the value of $h(f(e^2 ))$?
$3+\log_e(e+1)$ | |
$2-\log_e(e-1)$ | |
$3-\log_e(e+1)$ | |
$3+\log_e(1-e)$ |
Question 11 Explanation:
The correct answer is (A).
$h(f(x))$
$=h(x(x+e))$
$=\log_e \ x(x+e)$
Thus, for $x=e^2$
$h(f(e^2 ))$
$=\log_e \ e^2 (e^2+e)$
$=\log_e \ e^3 (e+1)$
$=3\ \log_e \ e+\log_e(e+1) $
$=3+\log_e(e+1)$
$h(f(x))$
$=h(x(x+e))$
$=\log_e \ x(x+e)$
Thus, for $x=e^2$
$h(f(e^2 ))$
$=\log_e \ e^2 (e^2+e)$
$=\log_e \ e^3 (e+1)$
$=3\ \log_e \ e+\log_e(e+1) $
$=3+\log_e(e+1)$
Question 12 |
Andy works out the inverse of the function $f(x)=2^{2x+1}$. What would the graph of $f^{-1} (x)$ look like when he plots it?
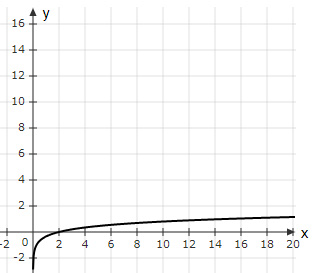 | |
 | |
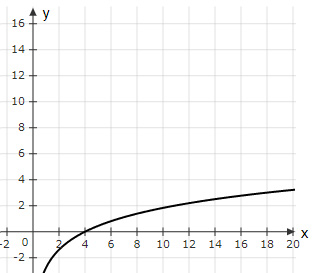 | |
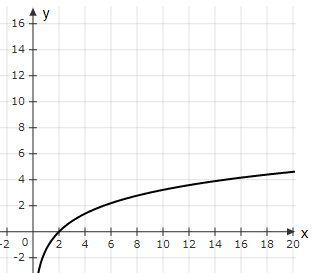 |
Question 12 Explanation:
The correct answer is (A).
$y=f(x)=2^{2x+1}$
$\log_2 \ y=2x+1$
$x=\dfrac{1}{2} (\log_2 \ y-1)$
In terms of $x$,
$f^{-1} (x)=\dfrac{1}{2} (\log_2 \ x-1)$
Option (A) → Best fit (Correct Graph)
Option (B) → $f^{-1} (2)≠0$ (Incorrect Graph)
Option (C) → $f^{-1} (2)≠0$ (Incorrect Graph)
Option (D) → $f^{-1} (8)≠1$ (Incorrect Graph)
$y=f(x)=2^{2x+1}$
$\log_2 \ y=2x+1$
$x=\dfrac{1}{2} (\log_2 \ y-1)$
In terms of $x$,
$f^{-1} (x)=\dfrac{1}{2} (\log_2 \ x-1)$
Option (A) → Best fit (Correct Graph)
Option (B) → $f^{-1} (2)≠0$ (Incorrect Graph)
Option (C) → $f^{-1} (2)≠0$ (Incorrect Graph)
Option (D) → $f^{-1} (8)≠1$ (Incorrect Graph)
Question 13 |
Work out the domain of the function $\log_x(x^2-5)$.
$(-\sqrt{5},∞)$ | |
$(\sqrt{5},∞)$ | |
$(-\sqrt{5},\sqrt{5})$ | |
$(6,∞)$ |
Question 13 Explanation:
The correct answer is (B).
$\log_b \ a$ is defined for $b>0, b≠1$ and $a>0$
Thus, for $\log_x(x^2-5)$
$x>0$ and $x≠1$
While, $x^2-5>0→x>\sqrt{5}$
$(\text{rejecting} \; x<-\sqrt{5} \, \text{ as}$ $ \ x>0)$
Thus, $x∈(\sqrt{5},∞) $
$\log_b \ a$ is defined for $b>0, b≠1$ and $a>0$
Thus, for $\log_x(x^2-5)$
$x>0$ and $x≠1$
While, $x^2-5>0→x>\sqrt{5}$
$(\text{rejecting} \; x<-\sqrt{5} \, \text{ as}$ $ \ x>0)$
Thus, $x∈(\sqrt{5},∞) $
Question 14 |
Determine the inverse of the function $f(x)=\log_6(x+8)$.
$8.6^x$ | |
$\frac{1}{8} 6^x$ | |
$6^x+8$ | |
$6^x-8$ |
Question 14 Explanation:
The correct answer is (D).
$y=f(x)=\log_6(x+8)$
$x+8=6^y$
$x=6^y-8$
In terms of $x$,
$y=f^{-1} (x)=6^x-8$
$y=f(x)=\log_6(x+8)$
$x+8=6^y$
$x=6^y-8$
In terms of $x$,
$y=f^{-1} (x)=6^x-8$
Question 15 |
The table below shows the function $h(x)$.
$X$ |
$1$ |
$2$ |
$4$ |
$6$ |
$9$ |
$h(x)$ |
$5$ |
$10$ |
$20$ |
$100$ |
$200$ |
Another function $g(x)$ is equal to $\log_{10}(x)+x^2$. What is the value of $g(h (2))$?
$5$ | |
$10$ | |
$26$ | |
$101$ |
Question 15 Explanation:
The correct answer is (D).
From the table, $h(2)=10$
Thus, $g(h(2))=g(10)$
$g(10)=\log_{10}(10)+10^2 $ $ =1+100=101$
From the table, $h(2)=10$
Thus, $g(h(2))=g(10)$
$g(10)=\log_{10}(10)+10^2 $ $ =1+100=101$
Question 16 |
The graph below shows the first $5$ terms of an Arithmetic Progression.
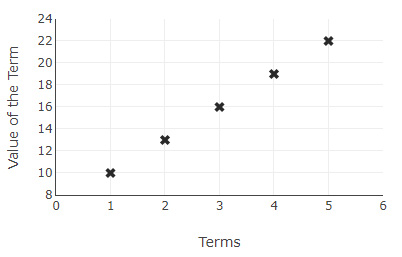
What would be the $n$th term of a Geometric Progression with the same first term $a$ and with a common ratio $r$ equal to the common difference $d$ of the Arithmetic Progression?
(Note: $n$ takes on integer values $1,2,3…$ in the formulae below)
$10(3)^{n-1}$ | |
$3(3)^n$ | |
$10(3)^{n+1}$ | |
$30(3)^{n-1}$ |
Question 16 Explanation:
The correct answer is (A).
From the graph, sequence is $10,13,16,19,22,…$
First term $=a=10$
Common ratio $r=$ Common difference $d=13-10=3$
Thus, the $n$th term $=a(r)^{n-1}=10(3)^{n-1}$
From the graph, sequence is $10,13,16,19,22,…$
First term $=a=10$
Common ratio $r=$ Common difference $d=13-10=3$
Thus, the $n$th term $=a(r)^{n-1}=10(3)^{n-1}$
Question 17 |
The two arithmetic progressions below have their 5th terms equal.
$S_1: T_n=10-4(n-1)$
$S_2:T_n=p+2(n-1)$
What is the sum of the first 5 terms for sequence $S_2$?
$−54$ | |
$−57$ | |
$−50$ | |
$−44$ |
Question 17 Explanation:
The correct answer is (C).
The 5th term of sequence $S_1$ is given by,
$T_5=10-4(5-1) $ $ =10-16=-6$
For sequence $S_2$,
$T_5= p + 2(5 − 1) = p + 8$
Thus,
$p + 8 = −6$
$p= −14$
The $n$th term of sequence $S_2 \,$ is: $\, T_n=-14+2(n-1)$
Here, $a=-14$ and $d=2$
Sum of first 5 terms is given by,
$\dfrac{n}{2} [2a+(n-1)d]$
$=\dfrac{5}{2} [-28+4×2]$
$=-5×10 $
$=-50$
The 5th term of sequence $S_1$ is given by,
$T_5=10-4(5-1) $ $ =10-16=-6$
For sequence $S_2$,
$T_5= p + 2(5 − 1) = p + 8$
Thus,
$p + 8 = −6$
$p= −14$
The $n$th term of sequence $S_2 \,$ is: $\, T_n=-14+2(n-1)$
Here, $a=-14$ and $d=2$
Sum of first 5 terms is given by,
$\dfrac{n}{2} [2a+(n-1)d]$
$=\dfrac{5}{2} [-28+4×2]$
$=-5×10 $
$=-50$
Question 18 |
Look at the sequence below.
$\log_{10}x, \log_{10}x^3 , \log_{10}x^5 , … $
$S_n (x)$ is defined as the sum of the first $n$ terms of the sequence. Work out the formula for $S_n (10)$.
$n^2$ | |
$n^2-n$ | |
$n^2+n$ | |
$2n^2+1$ |
Question 18 Explanation:
The correct answer is (A). For the sequence given,
First term $=a=\log_{10}x$
Difference of first two terms
$ =d_1=\log_{10}x^3 -\log_{10}x $ $ =2 \ \log_{10}x $
Difference of next two terms
$=d_2=\log_{10}x^5 -\log_{10}x^3 $ $ =2 \ \log_{10}x $
Thus, the sequence is an AP (Arithmetic Progression)
Sum $S_n (x)$
$=\dfrac{n}{2} [2a+(n-1)d]$
$=\dfrac{n}{2}[2 \ \log_{10}x+2(n-1) $ $ \log_{10}x] $
$=n\log_{10}x [1+(n-1)]$
$=n^2\log_{10}x $
$S_n (10)=n^2\log_{10}10=n^2 $
First term $=a=\log_{10}x$
Difference of first two terms
$ =d_1=\log_{10}x^3 -\log_{10}x $ $ =2 \ \log_{10}x $
Difference of next two terms
$=d_2=\log_{10}x^5 -\log_{10}x^3 $ $ =2 \ \log_{10}x $
Thus, the sequence is an AP (Arithmetic Progression)
Sum $S_n (x)$
$=\dfrac{n}{2} [2a+(n-1)d]$
$=\dfrac{n}{2}[2 \ \log_{10}x+2(n-1) $ $ \log_{10}x] $
$=n\log_{10}x [1+(n-1)]$
$=n^2\log_{10}x $
$S_n (10)=n^2\log_{10}10=n^2 $
Question 19 |
The first 5 terms of a sequence are shown as follows.

When a smooth line is drawn joining these points, which function would it be proportional to?
$\log_2 \ x$ | |
$2^x $ | |
$x^2$ | |
None of these |
Question 19 Explanation:
The correct answer is (B). The value of the term doubles at every integer.
So, the function must be proportional to $2^x$.
So, the function must be proportional to $2^x$.
Question 20 |
$ka^x$ and $mb^x$ are two exponential functions such that $1 < a < b < 10$ and $0 < m < k < 1 $. Find the value of $x$ for which $ka^x$ is equal to $mb^x$.
$x=\dfrac{\log_{10}a/b}{\log_{10}m/k}$ | |
$x=\dfrac{2\log_{10}m/k }{\log_{10}a/b}$ | |
$x=\dfrac{\log_{10}(m-k)}{\log_{10}(a-b)} $ | |
$x=\dfrac{\log_{10}m/k}{ \log_{10}a/b}$ |
Question 20 Explanation:
The correct answer is (D).
$ka^x= mb^x$
$\left(\dfrac{a}{b}\right)^x=\dfrac{m}{k} $
Thus,
$x\log_{10}\dfrac{a}{b}=\log_{10}\dfrac{m}{k}$
$x=\dfrac{\log_{10}m/k}{ \log_{10}a/b} $
$ka^x= mb^x$
$\left(\dfrac{a}{b}\right)^x=\dfrac{m}{k} $
Thus,
$x\log_{10}\dfrac{a}{b}=\log_{10}\dfrac{m}{k}$
$x=\dfrac{\log_{10}m/k}{ \log_{10}a/b} $
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 20 questions to complete.
|
List |
Next Practice Test:
AP Precalculus Unit 3 >>
AP Precalculus Main Menu >>
