The below test will be based on the trigonometric function definitions and their values in four quadrants. Also, finding the values of other trigonometric functions given one, their graphs, and their inverses. Conversion of cartesian and polar coordinates is included as a prerequisite for later questions on polar graphs of the form $r(θ)$.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
The expression $\text{cosec } A + \cotA $ is equal to,
$\dfrac{1 + \cos A}{\sin A}$ | |
$\dfrac{1 + \tan A}{1 - \cot A}$ | |
$\dfrac{1}{1 + \tan A}$ | |
$\dfrac{\sin A}{1 + \cos A}$ |
Question 1 Explanation:
The correct answer is (A).
$\text{cosec} \ A + \cot A $
$ =\dfrac{1}{\sin A} + \dfrac{\cos A}{\sin A}$
$=\dfrac{1 + \cos A}{\sin A}$
$\text{cosec} \ A + \cot A $
$ =\dfrac{1}{\sin A} + \dfrac{\cos A}{\sin A}$
$=\dfrac{1 + \cos A}{\sin A}$
Question 2 |
The cartesian coordinates $(x,y)$ corresponding to the polar coordinates $(4,\frac{3π}{4})$ are,
$(2 \sqrt{2},2 \sqrt{2})$ | |
$(-\sqrt{2}, 2 \sqrt{2})$ | |
$(-2 \sqrt{2}, 2 \sqrt{2})$ | |
$(-2, 2 \sqrt{2})$ |
Question 2 Explanation:
The correct answer is (C).
$x=r \cos θ \ $ and $ \ y=r \ \sin θ$
Thus, for $(r,θ)=\left(4,\dfrac{3π}{4}\right),$
$x=4 \cos\dfrac{3π}{4} \ $ and $ \ y=4 \sin \dfrac{3π}{4}$
$x=4×\left(-\dfrac{1}{\sqrt{2}}\right) \ $ and $ \ y=4×\left(\dfrac{1}{\sqrt{2}}\right)$
$x=-2 \sqrt{2} \ $ and $ \ y=2 \sqrt{2}$
$x=r \cos θ \ $ and $ \ y=r \ \sin θ$
Thus, for $(r,θ)=\left(4,\dfrac{3π}{4}\right),$
$x=4 \cos\dfrac{3π}{4} \ $ and $ \ y=4 \sin \dfrac{3π}{4}$
$x=4×\left(-\dfrac{1}{\sqrt{2}}\right) \ $ and $ \ y=4×\left(\dfrac{1}{\sqrt{2}}\right)$
$x=-2 \sqrt{2} \ $ and $ \ y=2 \sqrt{2}$
Question 3 |
For some angle $θ$, $\sin θ = \frac{8}{17}$. If the terminal side is in the 2nd quadrant, what is the value of $\tan θ + \cot θ$?
$-\dfrac{298}{120}$ | |
$-\dfrac{289}{120}$ | |
$-\dfrac{256}{120}$ | |
$-\dfrac{267}{120}$ |
Question 3 Explanation:
The correct answer is (B).
Using $\sin^2 θ+\cos^2 θ=1$
$\cos^2 θ=1-\dfrac{64}{289}=\dfrac{225}{289} $
$\cos θ=-\dfrac{15}{17}$ (as $θ$ is between $\frac{π}{2}$ and $π$)
$\tan θ+\cot θ $
$=\dfrac{\sin θ}{\cos θ} +\dfrac{\cos θ}{\sin θ}$
$=\dfrac{1}{\sinθ \cosθ}$
$=1÷\left(\dfrac{8}{17}×-\dfrac{15}{17}\right)$
$=-\dfrac{289}{120}$
Using $\sin^2 θ+\cos^2 θ=1$
$\cos^2 θ=1-\dfrac{64}{289}=\dfrac{225}{289} $
$\cos θ=-\dfrac{15}{17}$ (as $θ$ is between $\frac{π}{2}$ and $π$)
$\tan θ+\cot θ $
$=\dfrac{\sin θ}{\cos θ} +\dfrac{\cos θ}{\sin θ}$
$=\dfrac{1}{\sinθ \cosθ}$
$=1÷\left(\dfrac{8}{17}×-\dfrac{15}{17}\right)$
$=-\dfrac{289}{120}$
Question 4 |
What is the amplitude and the period of the below trigonometric function?
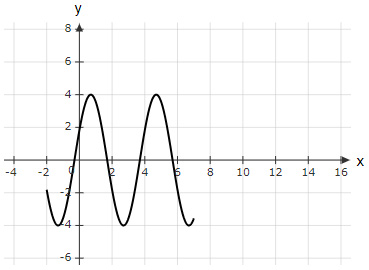
$\text{Amplitude} = 8 \ \text{ and }$ $\text{Period} = 4$ | |
$\text{Amplitude} = 8 \ \text{ and }$ $\text{Period} = 8$ | |
$\text{Amplitude} = 4 \ \text{ and }$ $\text{Period} = 6$ | |
$\text{Amplitude} = 4 \ \text{ and }$ $\text{Period} = 4$ |
Question 4 Explanation:
The correct answer is (D).
Distance from mean value to max value $=4-0=4 \text{ units}$
Amplitude $=4 \text{ units}$
The wave completes one oscillation in $4-0=4 \text{ units}$
Period $=4 \text{ units}$
Distance from mean value to max value $=4-0=4 \text{ units}$
Amplitude $=4 \text{ units}$
The wave completes one oscillation in $4-0=4 \text{ units}$
Period $=4 \text{ units}$
Question 5 |
If $\tan α = y$ where $α$ is an angle between $\dfrac{5π}{4}$ and $\dfrac{3π}{2}$, then what is $\cos α + \sin α$ equal to?
$\dfrac{(1+y)}{\sqrt{1-y^2}}$ | |
$\dfrac{(1-y)}{\sqrt{1+y^2}}$ | |
$ - \dfrac{(1-y)}{\sqrt{1+y^2}}$ | |
$ - \dfrac{(1+y)}{\sqrt{1+y^2}}$ |
Question 5 Explanation:
The correct answer is (D).
$α$ is in the 3rd Quadrant
$→\cos α$ and $\sin α$ are negative
$1+\tan^2 α=sec^2 α$
So, $\sec α=-\sqrt{1+y^2 } $ $ →\cos α=- \dfrac{1}{\sqrt{1+y^2}}$
And, $\sin α=-\sqrt{1-\left( \dfrac{1}{1+y^2 }\right) } $ $ =-\dfrac{y}{\sqrt{1+y^2}}$
$\sin α + \cos α=- \dfrac{1+y}{\sqrt{1+y^2}}$
$α$ is in the 3rd Quadrant
$→\cos α$ and $\sin α$ are negative
$1+\tan^2 α=sec^2 α$
So, $\sec α=-\sqrt{1+y^2 } $ $ →\cos α=- \dfrac{1}{\sqrt{1+y^2}}$
And, $\sin α=-\sqrt{1-\left( \dfrac{1}{1+y^2 }\right) } $ $ =-\dfrac{y}{\sqrt{1+y^2}}$
$\sin α + \cos α=- \dfrac{1+y}{\sqrt{1+y^2}}$
Question 6 |
For some angle $x, \sin x = -\dfrac{\sqrt{3}}{2}$ and $\sec x = 2$. Which option shows the size of angle $x$?
$\dfrac{11π}{6}$ | |
$\dfrac{4π}{3}$ | |
$\dfrac{5π}{3}$ | |
$\dfrac{2π}{3}$ |
Question 6 Explanation:
The correct answer is (C).
$\sin x$ is $-ive$ and $\cos x$ is $+ive$
Thus, angle $x$ is in the 4th Quadrant
Using $\sin x=-\dfrac{\sqrt{3}}{2} \ $ and $ \ \cos x=\dfrac{1}{2}$ on a unit circle,
$→x$ must be equal to $\dfrac{5π}{3}$
$\sin x$ is $-ive$ and $\cos x$ is $+ive$
Thus, angle $x$ is in the 4th Quadrant
Using $\sin x=-\dfrac{\sqrt{3}}{2} \ $ and $ \ \cos x=\dfrac{1}{2}$ on a unit circle,
$→x$ must be equal to $\dfrac{5π}{3}$
Question 7 |
$\tan \left(\dfrac{πx}{4}\right)$ is plotted on a graph paper for $x∈ \left(-\dfrac{5}{3},\dfrac{5}{3}\right)$. Which option shows the correct graph for the function?
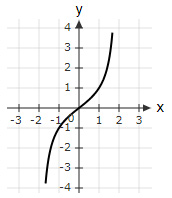 | |
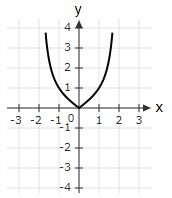 | |
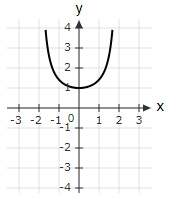 | |
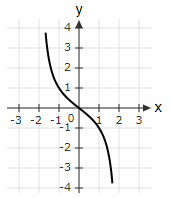 |
Question 7 Explanation:
The correct answer is (A).
$\tan \left(\dfrac{πx}{4}\right)$ is an odd function and is positive in the 1st Quadrant.
So, options (B), (C) and (D) are ruled out.
$\tan \left(\dfrac{πx}{4}\right)$ is an odd function and is positive in the 1st Quadrant.
So, options (B), (C) and (D) are ruled out.
Question 8 |
Two functions, $f(θ)$ and $g(θ)$, are defined as $\sqrt{2} \sin θ$ and $\sqrt{6} \cos θ$, respectively. If $ π < θ < 2π$, find $θ$ for which $f(θ)=g(θ)$.
$\dfrac{5π}{4}$ | |
$\dfrac{4π}{3}$ | |
$\dfrac{5π}{6}$ | |
$\dfrac{6π}{5}$ |
Question 8 Explanation:
The correct answer is (B).
$\sqrt{2} \sin θ=\sqrt{6} \cos θ$
$ → \tan θ=\sqrt{3}$
Using a unit circle,
$θ=\dfrac{π}{3}$ or $\dfrac{4π}{3}$
For $π < θ < 2π$, answer should be $\dfrac{4π}{3}$.
$\sqrt{2} \sin θ=\sqrt{6} \cos θ$
$ → \tan θ=\sqrt{3}$
Using a unit circle,
$θ=\dfrac{π}{3}$ or $\dfrac{4π}{3}$
For $π < θ < 2π$, answer should be $\dfrac{4π}{3}$.
Question 9 |
The polar coordinates $(r,θ)$ corresponding to the cartesian coordinates $(1,-\sqrt{3})$ are,
$\left(2, \dfrac{π}{3}\right)$ | |
$\left(2, \dfrac{2π}{3}\right)$ | |
$\left(2, \dfrac{5π}{3}\right)$ | |
$\left(2, \dfrac{4π}{3}\right)$ |
Question 9 Explanation:
The correct answer is (C).
$r=\sqrt{x^2+y^2} $ $ = \sqrt{1+3} =2$
$\cosθ= \dfrac{x}{r}=\dfrac{1}{2}$
$\sinθ=\dfrac{y}{r}=-\dfrac{\sqrt{3}}{2} $
Using a unit circle,
$θ = \dfrac{5π}{3}$
Polar coordinates $=\left(2, \dfrac{5π}{3}\right)$
$r=\sqrt{x^2+y^2} $ $ = \sqrt{1+3} =2$
$\cosθ= \dfrac{x}{r}=\dfrac{1}{2}$
$\sinθ=\dfrac{y}{r}=-\dfrac{\sqrt{3}}{2} $
Using a unit circle,
$θ = \dfrac{5π}{3}$
Polar coordinates $=\left(2, \dfrac{5π}{3}\right)$
Question 10 |
Look at the graph of $g(x)$.
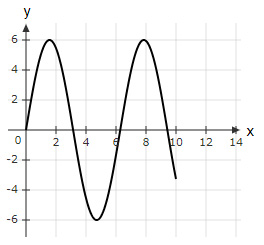
If the function $f(x)=\dfrac{x}{2}$ is drawn, for how many values of $x$ is $f(x)=g(x)$?
$4$ | |
$1$ | |
$2$ | |
$6$ |
Question 10 Explanation:
The correct answer is (A).
Plotting $\dfrac{x}{2}$ on the graph gives,
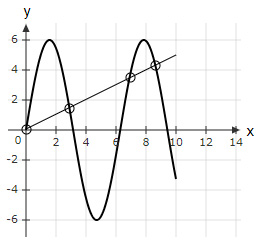
The number of points of intersection of the line and the graph is 4.
Thus, $f(x)$ and $g(x)$ are equal 4 times.
Plotting $\dfrac{x}{2}$ on the graph gives,

The number of points of intersection of the line and the graph is 4.
Thus, $f(x)$ and $g(x)$ are equal 4 times.
Question 11 |
What is the value of $\sin\left(\cos^{-1}\dfrac{1}{2}\right) + \sin \left(\cos^{-1}\dfrac{\sqrt{3}}{2}\right)$?
You may use a calculator.
$1.40$ | |
$1.37$ | |
$1.20$ | |
$1.11$ |
Question 11 Explanation:
The correct answer is (B).
$\sin\left(\cos^{-1} \dfrac{1}{2}\right)+\sin\left(\cos^{-1}\dfrac{\sqrt{3}}{2}\right)$
$=\sin \dfrac{π}{3}+\sin \dfrac{π}{6}$
$=\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}$
$=0.87+0.5$
$=1.37$
$\sin\left(\cos^{-1} \dfrac{1}{2}\right)+\sin\left(\cos^{-1}\dfrac{\sqrt{3}}{2}\right)$
$=\sin \dfrac{π}{3}+\sin \dfrac{π}{6}$
$=\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}$
$=0.87+0.5$
$=1.37$
Question 12 |
Which of the following options shows the range of $2(1 − 2 \cos x)$?
$[0,8]$ | |
$[-2,4]$ | |
$[-2,6]$ | |
$[0,6]$ |
Question 12 Explanation:
The correct answer is (C).
$-1 ≤ - \cosx≤1$
$-2 ≤ -2 \cos x≤2$
$-1 ≤ 1-2 \cos x≤3$
$-2 ≤ 2(1-2 \cos x )≤6$
Thus, the range of the function is $[-2,6]$.
$-1 ≤ - \cosx≤1$
$-2 ≤ -2 \cos x≤2$
$-1 ≤ 1-2 \cos x≤3$
$-2 ≤ 2(1-2 \cos x )≤6$
Thus, the range of the function is $[-2,6]$.
Question 13 |
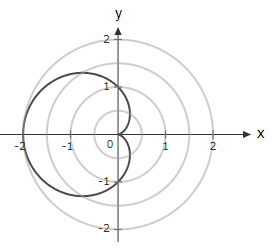
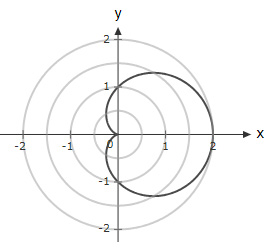
Which of the below graphs shows the polar function $r = 1 + \cos θ \ ?$
 | |
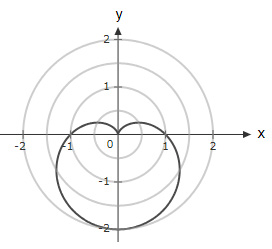
| |
 | |
 |
Question 13 Explanation:
The correct answer is (D).
$r=1+\cos θ$
Check values of $r$ for multiple values of $θ$ :
$r(0)=1+1=2 $
$r(π)=1-1=0$
$r\left(\dfrac{π}{2}\right)=1 + 0=1$
$r\left(\dfrac{3π}{2}\right)=1 + 0=1$
Which implies option (D) is true.
$r=1+\cos θ$
Check values of $r$ for multiple values of $θ$ :
$r(0)=1+1=2 $
$r(π)=1-1=0$
$r\left(\dfrac{π}{2}\right)=1 + 0=1$
$r\left(\dfrac{3π}{2}\right)=1 + 0=1$
Which implies option (D) is true.
Question 14 |
A polar function $r=1-\sin θ$ is plotted for $\dfrac{3π}{2} < θ < 2π$. Which of the below statements is true about the graph as we move from $\dfrac{3π}{2}$ to $2π$?
The points get closer to the origin | |
The points are below the $x$-axis and are at equal distance from the origin | |
The points are above the $x$-axis and keep moving towards the origin | |
The points get closer to the origin and then move away |
Question 14 Explanation:
The correct answer is (A).
For $r=1-\sin θ,$
Thus, the points are below the $x$-axis and get closer to the origin.
For $r=1-\sin θ,$
| $θ$ | $\dfrac{3π}{2}$ | $\dfrac{5π}{3}$ | $\dfrac{7π}{4}$ | $\dfrac{11π}{6}$ | $2π$ |
| $r(θ)$ | $2$ | $1.87$ | $1.71$ | $1.5$ | $1$ |
Question 15 |
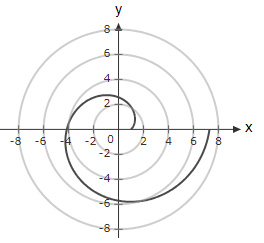
Which function could represent the below graph?
$r=1-2θ$ | |
$r=1-θ$ | |
$r=2+θ$ | |
$r=1+θ$ |
Question 15 Explanation:
The correct answer is (D).
Option (A):
$θ=0→ r=1$ & $θ=π →r=1-2π $ $ =-5.28$
(Incorrect function)
Option (B):
$θ=0→ r=1$ & $θ=π →r=1-π $ $ =-2.14$
(Incorrect function)
Option (C):
$θ=0→ r=2$
(Incorrect function)
Option (D):
$θ=0→ r=1 $ & $ θ=π →r=1+π $ $ =4.14$
(Correct function)
Option (A):
$θ=0→ r=1$ & $θ=π →r=1-2π $ $ =-5.28$
(Incorrect function)
Option (B):
$θ=0→ r=1$ & $θ=π →r=1-π $ $ =-2.14$
(Incorrect function)
Option (C):
$θ=0→ r=2$
(Incorrect function)
Option (D):
$θ=0→ r=1 $ & $ θ=π →r=1+π $ $ =4.14$
(Correct function)
Question 16 |
For what values of $θ$ is $\cos θ < -\dfrac{1}{2}$ and $\sinθ > - \dfrac{1}{\sqrt{2}} \ ?$
(Note: $π < θ < 2π$)
$π < θ < \dfrac{7π}{6}$ | |
$\dfrac{5π}{4} < θ < \dfrac{3π}{2}$ | |
$π < θ < \dfrac{5π}{4}$ | |
$π < θ < \dfrac{3π}{2}$ |
Question 16 Explanation:
The correct answer is (C).
Using a unit circle,
$\sinθ>-\dfrac{1}{\sqrt{2}} → θ < \dfrac{5π}{4} \ $ OR $ \ θ > \dfrac{7π}{4}$
$\cos θ< - \dfrac{1}{2} → θ < \dfrac{4π}{3} \ $ AND $ \ θ > \dfrac{2π}{3}$
Thus, in the interval $π < θ < 2π,$
$π < θ < \dfrac{5π}{4} $
Using a unit circle,
$\sinθ>-\dfrac{1}{\sqrt{2}} → θ < \dfrac{5π}{4} \ $ OR $ \ θ > \dfrac{7π}{4}$
$\cos θ< - \dfrac{1}{2} → θ < \dfrac{4π}{3} \ $ AND $ \ θ > \dfrac{2π}{3}$
Thus, in the interval $π < θ < 2π,$
$π < θ < \dfrac{5π}{4} $
Question 17 |
If $g(y)=\sin(2y+\dfrac{π}{12})$, then which of the below domains guarantees the existence of an inverse?
$-\dfrac{13π}{24} < y < \dfrac{11π}{24}$ | |
$-\dfrac{13π}{12} < y < \dfrac{11π}{12}$ | |
$0 < y < 2π$ | |
$-\dfrac{π}{2} < y < \dfrac{3π}{4}$ |
Question 17 Explanation:
The correct answer is (A). Inverse of a trigonometric function exists only when the domain of the function is restricted to an interval of $2π$.
$2y + \dfrac{π}{12} ∈ (-π,π)$
$-π < 2y + \dfrac{π}{12} < π$
$-\dfrac{13π}{12} < 2y < \dfrac{11π}{12}$
$-\dfrac{13π}{24} < y < \dfrac{11π}{24}$
$2y + \dfrac{π}{12} ∈ (-π,π)$
$-π < 2y + \dfrac{π}{12} < π$
$-\dfrac{13π}{12} < 2y < \dfrac{11π}{12}$
$-\dfrac{13π}{24} < y < \dfrac{11π}{24}$
Question 18 |
The temperature of a city during winters can be modeled using a function of the form $f(t)=300-100 \sin \left(\dfrac{πt}{45}\right)$, where $t$ is a specific winter day (typically between 1 and 90).
What is the trend in the city temperature on the 22nd day?
You may use a calculator.
The temperature is falling down at an increasing rate | |
The temperature is falling down at a decreasing rate | |
The temperature is rising up at a decreasing rate | |
The temperature is rising up at an increasing rate |
Question 18 Explanation:
The correct answer is (B). A rough sketch of the temperature function for $t$ from $0$ to $90$ is:

As seen from the sketch, $t=22.5$ represents the lowest point on the graph.
Thus, for $t = 22$, the temperature is falling down at a decreasing rate.

As seen from the sketch, $t=22.5$ represents the lowest point on the graph.
Thus, for $t = 22$, the temperature is falling down at a decreasing rate.
Question 19 |
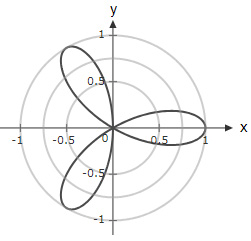
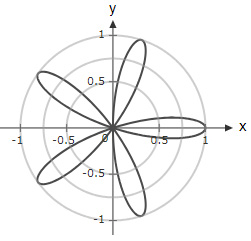
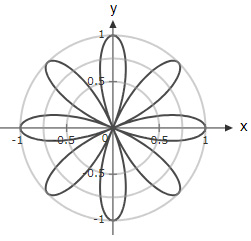
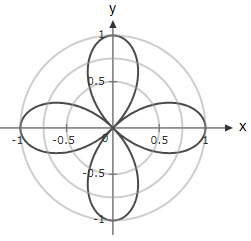
A rose curve is defined by the equation $r = \cos(2θ)$. Which option shows the graph of the function in the interval $(0,2π)$?
 | |
 | |
 | |
 |
Question 19 Explanation:
The correct answer is (D). Check values of $\cos(2θ)$ at different points on the graph:
For $θ=0, r(0)=1$
For $θ=\dfrac{π}{2}, r(\dfrac{π}{2})=-1$ (Which means $r=1$ in the opposite direction)
→ Option (A) and (B) are ruled out
For $θ=\dfrac{π}{4}, r(\dfrac{π}{4})=0$
→ Option (C) is ruled out
For $θ=0, r(0)=1$
For $θ=\dfrac{π}{2}, r(\dfrac{π}{2})=-1$ (Which means $r=1$ in the opposite direction)
→ Option (A) and (B) are ruled out
For $θ=\dfrac{π}{4}, r(\dfrac{π}{4})=0$
→ Option (C) is ruled out
Question 20 |
Which of the below expressions is equal to $\dfrac{\sin x}{1 - \cos x} \ ?$
$\dfrac{1 + \sin x}{\cos x} $ | |
$\dfrac{1 + \cos x}{\sin x} $ | |
$\dfrac{1 - \sin x}{\cos x} $ | |
$\dfrac{1 + 2 \sin x}{\cos x} $ |
Question 20 Explanation:
The correct answer is (B).
$\sin^2 x=1-\cos^2 x$
$\sin^2 x $ $ =(1-\cos x )(1+\cos x)$
Divide by $\sin x (1- \cos x)$ on both sides,
$\dfrac{\sin x}{1 - \cos x} = \dfrac{1 + \cos x}{\sin x} $
$\sin^2 x=1-\cos^2 x$
$\sin^2 x $ $ =(1-\cos x )(1+\cos x)$
Divide by $\sin x (1- \cos x)$ on both sides,
$\dfrac{\sin x}{1 - \cos x} = \dfrac{1 + \cos x}{\sin x} $
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 20 questions to complete.
|
List |
More Practice Tests:
AP Precalculus Main Menu >>
