In the below test, questions are based on the concepts of functions and their notations, graphs of functions, and operations (composition and inverse) on functions. Further, polynomials and rational functions are included along with their graphs and specific properties like roots, end behavior, and vertical and horizontal asymptotes.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
Which of the options below shows the domain of the function $f(x)$?
$f(x)=\dfrac{1}{\sqrt{x-\sqrt{2}}}$
$[\sqrt{2},∞)$ | |
$(\sqrt{2},∞)$ | |
$(-\sqrt{2},∞)$ | |
$[\sqrt{2},∞]$ |
Question 1 Explanation:
The correct answer is (B). To find the domain of the function $f(x)$ work out the values of $x$ for which $f(x)$ is well defined:
$f(x)=\dfrac{1}{\sqrt{x-\sqrt{2}}}$
$x-\sqrt{2}>0 $
$x>\sqrt{2} $
In interval notation, $x ∈(\sqrt{2},∞)$
$f(x)=\dfrac{1}{\sqrt{x-\sqrt{2}}}$
$x-\sqrt{2}>0 $
$x>\sqrt{2} $
In interval notation, $x ∈(\sqrt{2},∞)$
Question 2 |
Find the average rate of change of the function $g(x)$ from $x=2$ to $x=4$.
$g(x)=\dfrac{x}{x^2 - 1}$
$-\dfrac{1}{2}$ | |
$-\dfrac{3}{5}$ | |
$-\dfrac{1}{3}$ | |
$-\dfrac{1}{5}$ |
Question 2 Explanation:
The correct answer is (D). Average rate of change
$= \dfrac{g(4) - g(2)}{4 - 2}$
$= \left(\dfrac{4}{15} - \dfrac{2}{3}\right)×\dfrac{1}{2}$
$= -\dfrac{6}{15} × \dfrac{1}{2}$
$= -\dfrac{1}{5}$
$= \dfrac{g(4) - g(2)}{4 - 2}$
$= \left(\dfrac{4}{15} - \dfrac{2}{3}\right)×\dfrac{1}{2}$
$= -\dfrac{6}{15} × \dfrac{1}{2}$
$= -\dfrac{1}{5}$
Question 3 |
Find all the roots of the polynomial function $p(x)=x^3-3x^2+4$.
$1,2,-1$ | |
$-2,-1,0$ | |
$-2,1,1$ | |
$-1,2,2$ |
Question 3 Explanation:
The correct answer is (D).
Method I: Check each option by substitution
Method II: Factorize
$x^3-3x^2+4$
$=x^3+x^2-4x^2+4$
$=x^2 (x+1)-4(x^2-1)$
$=x^2 (x+1)-4(x+1)(x-1)$
$=(x+1)(x^2-4x+4)$
$=(x+1) (x-2)^2$
$=0$
$→x=-1\ \,$ or $\, \ x=2,2 $
Method I: Check each option by substitution
Method II: Factorize
$x^3-3x^2+4$
$=x^3+x^2-4x^2+4$
$=x^2 (x+1)-4(x^2-1)$
$=x^2 (x+1)-4(x+1)(x-1)$
$=(x+1)(x^2-4x+4)$
$=(x+1) (x-2)^2$
$=0$
$→x=-1\ \,$ or $\, \ x=2,2 $
Question 4 |
A function $f(x)$, when plotted on a graph paper, looks as shown below.
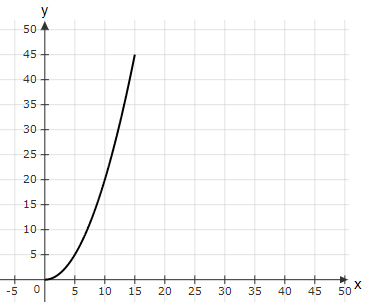
What is $f^{-1} (20)$ equal to?
$15$ | |
$10$ | |
$7.5$ | |
$12.5$ |
Question 4 Explanation:
The correct answer is (B).
$f^{-1} (y)=x→y=f(x)=20$
From the graph, $f(x)$ is equal to 20 when $x$ is 10.
$f^{-1} (y)=x→y=f(x)=20$
From the graph, $f(x)$ is equal to 20 when $x$ is 10.
Question 5 |
If $h(x)=x^2-5$, then what is the value of $h(h(x))$?
$x^4-20x^2+20$ | |
$x^4-10x^2+25$ | |
$x^4-10x^2+20$ | |
$2x^4-10x^2+20$ |
Question 5 Explanation:
The correct answer is (C).
$h(x)=x^2-5$
Thus,
$h(h(x))$
$=h(x^2-5)$
$=(x^2-5)^2-5$
$=x^4-10x^2+25-5$
$=x^4-10x^2+20$
$h(x)=x^2-5$
Thus,
$h(h(x))$
$=h(x^2-5)$
$=(x^2-5)^2-5$
$=x^4-10x^2+25-5$
$=x^4-10x^2+20$
Question 6 |
The function $h(x)=x^2$ is moved horizontally by $3$ units to the right, then stretched vertically by a factor of $2$, and then moved vertically up by $6$ units. Which of the below equations shows the function after the transformations?
$h'(x)=2(x-3)^2+12$ | |
$h'(x)=(2x-3)^2+6$ | |
$h'(x)=2(x+6)^2-3$ | |
$h'(x)=2(x-3)^2+6$ |
Question 6 Explanation:
The correct answer is (D).
$h(x)=x^2$
After horizontal translation of 3 units (right):
$(x-3)^2$
After vertical stretch by 2 units:
$2(x-3)^2$
After vertical translation of 6 units (up):
$h'(x)=2(x-3)^2+6$
$h(x)=x^2$
After horizontal translation of 3 units (right):
$(x-3)^2$
After vertical stretch by 2 units:
$2(x-3)^2$
After vertical translation of 6 units (up):
$h'(x)=2(x-3)^2+6$
Question 7 |
Work out the equation of the line of best fit for the points in the table below:
| $X$ | $0$ | $2.5$ | $4$ | $5.8$ | $6.8$ | $8$ |
| $Y$ | $11$ | $18$ | $24$ | $33$ | $39$ | $43$ |
You may use a calculator.
$Y=4.18X+9.119$ | |
$Y=4.00X+10.201$ | |
$Y=3.24X+11.212$ | |
$Y=5.12X+9.021$ |
Question 7 Explanation:
The correct answer is (A). Input the $X$ values as List1(L1) and $Y$ values as List2(L2) into the calculator.
Use the Linear Regression module on the calculator to find the line of best fit.
The equation of the line is,
$Y=4.18X+9.119 $
Use the Linear Regression module on the calculator to find the line of best fit.
The equation of the line is,
$Y=4.18X+9.119 $
Question 8 |
Which graph shows a one-to-one function?
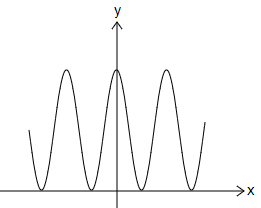 | |
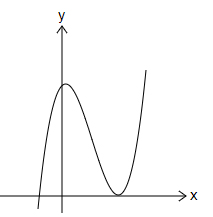 | |
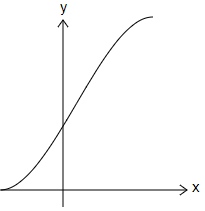 | |
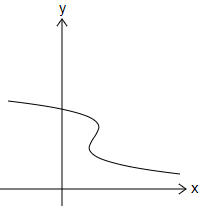 |
Question 8 Explanation:
The correct answer is (C). To find whether a function is one-to-one, draw a horizontal line and check how many times it cuts the graph:
Option (A) → More than 1 time (Not one-to-one).
Option (B) → More than 1 time (Not one-to-one).
Option (C) → Exactly 1 time (one-to-one).
Option (D) → The graph does not represent a function (It fails the vertical line test).
Option (A) → More than 1 time (Not one-to-one).
Option (B) → More than 1 time (Not one-to-one).
Option (C) → Exactly 1 time (one-to-one).
Option (D) → The graph does not represent a function (It fails the vertical line test).
Question 9 |
$f(x)=2x+7$ and $g(x)=ax-b$. What is the value of $a+b$ if $f(x)$ and $g(x)$ are inverses of each other?
$3$ | |
$4$ | |
$2$ | |
$1$ |
Question 9 Explanation:
The correct answer is (B). Since $f(x)$ and $g(x)$ are inverses of each other,
$f(g(x))=x$
Left hand side of the above equation
$=f(ax-b)$
$=2(ax-b)+7$
$=2ax+(-2b+7)$
$=x$
Thus,
$2a=1→a=\dfrac{1}{2}$
And, $2b-7=0→b=\dfrac{7}{2}$
$a+b=\dfrac{1}{2}+\dfrac{7}{2}=4$
$f(g(x))=x$
Left hand side of the above equation
$=f(ax-b)$
$=2(ax-b)+7$
$=2ax+(-2b+7)$
$=x$
Thus,
$2a=1→a=\dfrac{1}{2}$
And, $2b-7=0→b=\dfrac{7}{2}$
$a+b=\dfrac{1}{2}+\dfrac{7}{2}=4$
Question 10 |
Identify the polynomial from the graph shown below.
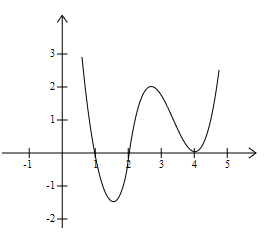
$(x-1)^2 (x-2)(x-4)$ | |
$(x-1)(x-2) (x-4)^2$ | |
$(x-1) (x-2)^2 (x-4)^2$ | |
$(x-1)^2 (x-2)^2 (x-4)$ |
Question 10 Explanation:
The correct answer is (B).
Thus, the polynomial must be of the form:
$(x-1)(x-2) (x-4)^2$
| $x=1$ | $x=2$ | $x=4$ |
| Crosses $x-axis$ | Crosses $x-axis$ | Tangent to $x-axis$ |
| Multiplicity should be odd $(1,3,5…)$ | Multiplicity should be odd $(1,3,5…)$ | Multiplicity should be even $(0,2,4,..)$ |
$(x-1)(x-2) (x-4)^2$
Question 11 |
The population of lions in a sanctuary is equal to 2,060 in 2002. In 2007, the population of lions increased to 2,880. When will the population of lions cross 4,000?
(Assume a linear model for the question)
You may use a calculator.
$2019$ | |
$2018$ | |
$2013$ | |
$2014$ |
Question 11 Explanation:
The correct answer is (D).
$\text{Slope} = \dfrac{2{,}880 − 2{,}060}{2007 − 2002} $ $ =164$
Thus, the population $p(t)=164t+2{,}060$ (where $t$ is the number of years after 2002)
To find the year in which $p(t)$ crosses 4,000, use: $164t+2,060=4,000$
$t=\dfrac{4{,}000-2{,}060}{164} $ $ = 11.82 ≈12 \text{ years}$
Thus, the population of lions cross 4,000 by: $2002+12=2014$
$\text{Slope} = \dfrac{2{,}880 − 2{,}060}{2007 − 2002} $ $ =164$
Thus, the population $p(t)=164t+2{,}060$ (where $t$ is the number of years after 2002)
To find the year in which $p(t)$ crosses 4,000, use: $164t+2,060=4,000$
$t=\dfrac{4{,}000-2{,}060}{164} $ $ = 11.82 ≈12 \text{ years}$
Thus, the population of lions cross 4,000 by: $2002+12=2014$
Question 12 |
Find the values of $x$ for which the inequality $6x^2-5x < x^3$ is true.
$(0,1) \cup (5,∞)$ | |
$\left(0,\frac{1}{2}\right)∪ [5,∞)$ | |
$(5,∞)$ | |
$(0,1)$ |
Question 12 Explanation:
The correct answer is (A).
$x^3>6x^2-5x$
$x^3-6x^2+5x>0$
$x(x^2-6x+5)>0$
$x(x-5)(x-1)>0$
Thus, $x>5 \,$ OR $\, 0< x <1$
$→x∈(0,1)∪(5,∞)$
$x^3>6x^2-5x$
$x^3-6x^2+5x>0$
$x(x^2-6x+5)>0$
$x(x-5)(x-1)>0$
Thus, $x>5 \,$ OR $\, 0< x <1$
$→x∈(0,1)∪(5,∞)$
Question 13 |
A polynomial has degree 10 with the leading coefficient $(a_{10})>0$. Which of the below statements is FALSE regarding the polynomial?
There are 9 local extrema of the polynomial at max | |
There are 10 roots of the polynomial at max | |
The polynomial goes to +∞ as $x$→±∞ | |
The polynomial must have 5 roots each with a multiplicity of 2 |
Question 13 Explanation:
The correct answer is (D).
Option (A) → A polynomial with degree 10 has 10 − 1 = 9 local extrema at max. (True)
Option (B) → A polynomial with degree 10 has 10 roots at max. (True)
Option (C) → Since the leading coefficient $a_{10}$ > 0 the polynomial increases as $x$→±∞. (True)
Option (D) → The polynomial may or may not have 5 roots of multiplicity 2. (False)
Option (A) → A polynomial with degree 10 has 10 − 1 = 9 local extrema at max. (True)
Option (B) → A polynomial with degree 10 has 10 roots at max. (True)
Option (C) → Since the leading coefficient $a_{10}$ > 0 the polynomial increases as $x$→±∞. (True)
Option (D) → The polynomial may or may not have 5 roots of multiplicity 2. (False)
Question 14 |
A polynomial $p(x)$ of degree 4 has real coefficients. If $p(x=2)=-6 \,$ and $\, p(x=6)=1$, then which of the statements below is correct? (Assume all the roots of the polynomial are distinct.)
There is at least 1 root in the interval [−6, 1] | |
There are 3 roots in the interval [−6, 1] | |
There are 1 or 3 roots in the interval [2, 6] | |
There are exactly 3 roots in the interval [2, 6] |
Question 14 Explanation:
The correct answer is (C).
[−6,1] represents the output interval of the polynomial. Thus, option (A) and (B) are ruled out.
Since, $p(x=2)=-6$ and $p(x=6)=1$
Thus, the polynomial must cross 0 at least once in the interval.
The degree of the polynomial is 4, so it can cross the $x$-axis a maximum of 3 times and a minimum of 1 time within the interval (odd number of times because the end values are negative and positive).
Which implies option (C) is correct.
[−6,1] represents the output interval of the polynomial. Thus, option (A) and (B) are ruled out.
Since, $p(x=2)=-6$ and $p(x=6)=1$
Thus, the polynomial must cross 0 at least once in the interval.
The degree of the polynomial is 4, so it can cross the $x$-axis a maximum of 3 times and a minimum of 1 time within the interval (odd number of times because the end values are negative and positive).
Which implies option (C) is correct.
Question 15 |
Which option shows the graph of the rational function $\dfrac{1}{x - 6}$?
 | |
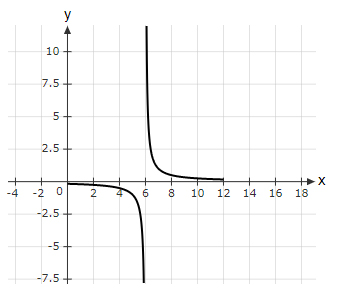 | |
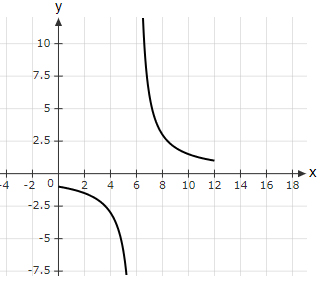 | |
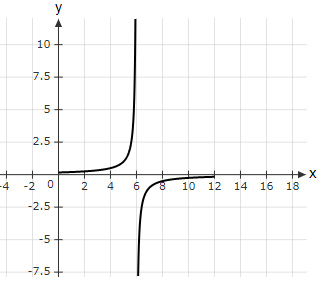 |
Question 15 Explanation:
The correct answer is (B).
Option (A) → Vertical asymptote at $x$ = 6 is missing (Incorrect graph).
Option (B) → Best fit (correct graph).
Option (C) → Value of the function at $x$ = 8 is bigger than expected value of 0.5 (Incorrect graph).
Option (D) → For $x$ < 6 the graph should be negative (Incorrect graph).
Option (A) → Vertical asymptote at $x$ = 6 is missing (Incorrect graph).
Option (B) → Best fit (correct graph).
Option (C) → Value of the function at $x$ = 8 is bigger than expected value of 0.5 (Incorrect graph).
Option (D) → For $x$ < 6 the graph should be negative (Incorrect graph).
Question 16 |
Which of the below rational functions have $y=2$ as an asymptote?
$y=\dfrac{x^2 - 3}{x + 10}$ | |
$y=\dfrac{x - 3}{x + 10}$ | |
$y=\dfrac{2x^2 - 3}{x^2 + 10}$ | |
$y=\dfrac{x^3 - 3}{x + 100}$ |
Question 16 Explanation:
The correct answer is (C).
For the rational function $\dfrac{P(x)}{Q(x)}$, when $P(x)$ and $Q(x)$ are of equal degree, then there exists a horizontal asymptote of the form $y$=constant.
So, Options (A) and (D) are ruled out.
Option (B)
$ → y= \lim\limits_{x\to ∞} \dfrac{x - 3}{x + 10} $ $ = \lim\limits_{x\to ∞} \dfrac{1-3/x}{1+10/x}$
$=\dfrac{1-0}{1+0}=1$
Option (C)
$ → y= \lim\limits_{x\to ∞} \dfrac{2x^2 - 3}{x^2 + 10} $ $ = \lim\limits_{x\to ∞} \dfrac{2-3/x^2}{1+10/x^2}$
$=\dfrac{2-0}{1+0}=2$
For the rational function $\dfrac{P(x)}{Q(x)}$, when $P(x)$ and $Q(x)$ are of equal degree, then there exists a horizontal asymptote of the form $y$=constant.
So, Options (A) and (D) are ruled out.
Option (B)
$ → y= \lim\limits_{x\to ∞} \dfrac{x - 3}{x + 10} $ $ = \lim\limits_{x\to ∞} \dfrac{1-3/x}{1+10/x}$
$=\dfrac{1-0}{1+0}=1$
Option (C)
$ → y= \lim\limits_{x\to ∞} \dfrac{2x^2 - 3}{x^2 + 10} $ $ = \lim\limits_{x\to ∞} \dfrac{2-3/x^2}{1+10/x^2}$
$=\dfrac{2-0}{1+0}=2$
Question 17 |
Work out the vertical asymptotes for the below function:
$\dfrac{x - 3}{x^2 - 5x - 14}$
$x=−2 \; \; \& \; -7$ | |
$x=−2 \; \; \& \;\; 7$ | |
$x=−2 \; \; \& \; \; 3$ | |
$x=3 \; \; \& \; \; 5$ |
Question 17 Explanation:
The correct answer is (B).
$\dfrac{x - 3}{x^2 − 5x − 14} $ $ =\dfrac{x − 3}{(x − 7)(x + 2)} $ $ =\dfrac{P(x)}{Q(x)}$
For $x=-2 \,$ and $\, x=7$
$P(x)≠0 \,$ and $\, Q(x)=0$
Thus, the vertical asymptotes are: $x =−2 \,$ and $\, 7$
$\dfrac{x - 3}{x^2 − 5x − 14} $ $ =\dfrac{x − 3}{(x − 7)(x + 2)} $ $ =\dfrac{P(x)}{Q(x)}$
For $x=-2 \,$ and $\, x=7$
$P(x)≠0 \,$ and $\, Q(x)=0$
Thus, the vertical asymptotes are: $x =−2 \,$ and $\, 7$
Question 18 |
Which line describes the end behavior asymptote for the function $g(x)=\dfrac{x^4 - 16}{x^3 - 8}$?
$y=x$ | |
$y=2x$ | |
$y=x+1$ | |
$y=x-2$ |
Question 18 Explanation:
The correct answer is (A). Divide $x^4-16$ by $x^3-8$, using long division:
$x^4-16 $ $ =x(x^3-8)+(8x-16) $
Thus, $\dfrac{x^4 - 16}{x^3 - 8} $ $ =x+\dfrac{8x - 16}{x^3 - 8}$
Hence, end behavior asymptote for the function is $y=x$.
$x^4-16 $ $ =x(x^3-8)+(8x-16) $
Thus, $\dfrac{x^4 - 16}{x^3 - 8} $ $ =x+\dfrac{8x - 16}{x^3 - 8}$
Hence, end behavior asymptote for the function is $y=x$.
Question 19 |
Work out the intervals on which $\dfrac{1}{x}<\dfrac{2}{2x -9}$.
$(-∞,1)∪(4,∞)$ | |
$(0,\frac{9}{2})$ | |
$(-∞,0)∪(\frac{9}{2},∞)$ | |
$(-∞,0)∪(5,∞)$ |
Question 19 Explanation:
The correct answer is (C).
$\dfrac{2}{2x - 9}>\dfrac{1}{x} $
$\dfrac{2}{2x - 9}-\dfrac{1}{x}>0 $
$\dfrac{2x}{x(2x -9)}-\dfrac{2x-9}{x(2x - 9)} >0 $
$\dfrac{9}{x(2x - 9)}>0$
Thus, $x>\dfrac{9}{2} \,$ OR $\, x<0$
Which implies $x∈(-∞,0)∪(\frac{9}{2},∞)$
$\dfrac{2}{2x - 9}>\dfrac{1}{x} $
$\dfrac{2}{2x - 9}-\dfrac{1}{x}>0 $
$\dfrac{2x}{x(2x -9)}-\dfrac{2x-9}{x(2x - 9)} >0 $
$\dfrac{9}{x(2x - 9)}>0$
Thus, $x>\dfrac{9}{2} \,$ OR $\, x<0$
Which implies $x∈(-∞,0)∪(\frac{9}{2},∞)$
Question 20 |
What should be the function equation that describes the graph shown below?
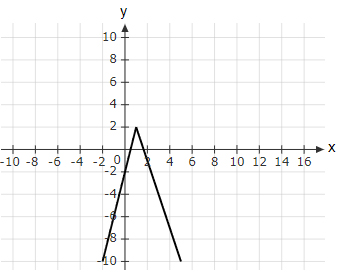
$ f(x) =
\begin{cases}
4x-2, &-2≤x≤1 \\
-3x+5,& \; \; \; 1≤x≤5
\end{cases}$ | |
$ f(x) =
\begin{cases}
4x-2, & \; \; \; -2≤x≤1 \\
2x-1,& \; \; \quad 1≤x≤5
\end{cases}$ | |
$ f(x) =
\begin{cases}
-3x+5, &-2≤x≤1 \\
4x+2,& \; \; \; 1≤x≤5
\end{cases}$ | |
$ f(x) =
\begin{cases}
4x-2, & \; \; \; -2≤x≤1 \\
3x+5,& \; \; \quad 1≤x≤5
\end{cases}$ |
Question 20 Explanation:
The correct answer is (A).
In the region $-2≤x≤1$,
Slope = $4$ and $y$-intercept = $- 2$
Equation is $f(x)=4x-2$
In the region $1≤x≤5$,
Slope = $- 3$ and $(1, 2)$ lies on the graph
Equation is $f(x)=-3x+5$
Thus, the function is,
$ f(x) = \begin{cases} 4x-2, &-2≤x≤1 \\ -3x+5,& \; \; \; 1≤x≤5 \end{cases}$
In the region $-2≤x≤1$,
Slope = $4$ and $y$-intercept = $- 2$
Equation is $f(x)=4x-2$
In the region $1≤x≤5$,
Slope = $- 3$ and $(1, 2)$ lies on the graph
Equation is $f(x)=-3x+5$
Thus, the function is,
$ f(x) = \begin{cases} 4x-2, &-2≤x≤1 \\ -3x+5,& \; \; \; 1≤x≤5 \end{cases}$
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 20 questions to complete.
|
List |
Next Practice Test:
AP Precalculus Unit 2 >>
AP Precalculus Main Menu >>
