A separate test on momentum is essential for AP Physics 1 preparation. The topics are mostly based on the concepts of internal and external forces of a system, the law of conservation of momentum, and impulse. Collisions are also included in the assessment as an application for the concept of system and momentum conservation. These concepts are needed to understand more involved topics studied later.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
Block A of mass $m_A$ is at rest, and Block B of mass $m_B$ travels at $u_B$ towards block A. The two blocks collide elastically and move in different directions.
Which of the below statements is FALSE?
The momentum of A increases and momentum of B decreases by the same amount | |
The two blocks move in opposite directions with equal momentum | |
The total kinetic energy of the system remains the same | |
The forces involved in the interaction are impulsive forces |
Question 1 Explanation:
The momentum of the system is conserved.
Option A → True
The two objects cannot move with equal momentum in opposite directions as net momentum of the system cannot be zero.
Option B → False
Kinetic energy is conserved in an elastic collision.
Option C → True
The forces act for very small amount of time.
Option D → True
Option A → True
The two objects cannot move with equal momentum in opposite directions as net momentum of the system cannot be zero.
Option B → False
Kinetic energy is conserved in an elastic collision.
Option C → True
The forces act for very small amount of time.
Option D → True
Question 2 |
A hard ball of mass $8.5\ kg$ falls from a height of $25\ m$. When it hits the ground, it rebounds to a height of $15\ m$. What is the magnitude of the impulse experienced by the ball upon striking the ground?
$201.7\ Ns$ | |
$289.5\ Ns$ | |
$345.8\ Ns$ | |
$337.3\ Ns$ |
Question 2 Explanation:
Velocity before striking the ground
$= v_i = \sqrt{2gh_i}$
$→ v_i = \sqrt{2×10×25} $ $ = 22.36\ m/s$
(pointing downwards)
Velocity after striking the ground
$= v_f = \sqrt{2gh_f}$
$→ v_f = \sqrt{2×10×15} $ $ = 17.32\ m/s$
(pointing upwards)
Impulse$ = Δp = mv_f-(-mv_i)$
($v_i$ points downwards)
$= mv_f+mv_i$
$= 8.5×(22.36+17.32)$
$= 337.3\ Ns$
$= v_i = \sqrt{2gh_i}$
$→ v_i = \sqrt{2×10×25} $ $ = 22.36\ m/s$
(pointing downwards)
Velocity after striking the ground
$= v_f = \sqrt{2gh_f}$
$→ v_f = \sqrt{2×10×15} $ $ = 17.32\ m/s$
(pointing upwards)
Impulse$ = Δp = mv_f-(-mv_i)$
($v_i$ points downwards)
$= mv_f+mv_i$
$= 8.5×(22.36+17.32)$
$= 337.3\ Ns$
Question 3 |
A toy of mass $1.1\ kg$ is moving with a speed of $3\ m/s$. It collides with a sticky object of mass $4.2\ kg$ at rest. The two objects stick with each other and move at the same speed.
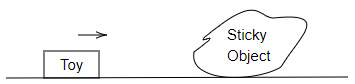
What is the combined speed of the toy and the sticky object?
$0.74\ m/s$ | |
$0.62\ m/s$ | |
$0.88\ m/s$ | |
$0.33\ m/s$ |
Question 3 Explanation:
Initial momentum = $1.1×3 = 3.3\ kgm/s$
Final momentum $= (1.1+4.2)v = 5.3v$
(where $v$ is the combined speed of the two objects)
Using conservation of momentum,
$5.3v = 3.3$
Thus, $v = \dfrac{3.3}{5.3} = 0.62\ m/s$
Final momentum $= (1.1+4.2)v = 5.3v$
(where $v$ is the combined speed of the two objects)
Using conservation of momentum,
$5.3v = 3.3$
Thus, $v = \dfrac{3.3}{5.3} = 0.62\ m/s$
Question 4 |
Miley multiplies the dimensions of the impulse with the dimensions of the velocity.
Which of the below quantities would have the same dimensions?
Power | |
Force per unit time | |
Work done | |
Force |
Question 4 Explanation:
Dimensions of Impulse $= Ns$ or $kgm/s$
Dimensions of velocity $= m/s$
→ Product $= kgm^2/s^2$ or $Nm$
Dimensions of work or energy are $Nm$
Dimensions of velocity $= m/s$
→ Product $= kgm^2/s^2$ or $Nm$
Dimensions of work or energy are $Nm$
Question 5 |
Questions 5, 6 and 7 are based on the information below.
A cube of mass $2\ kg$ is at the top of a twisting road, as shown below.
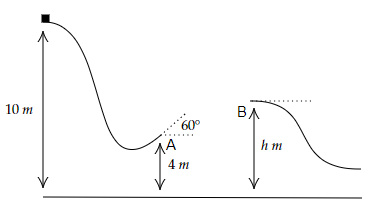
Bill gently pushes the cube into motion so that it travels the entire path. Ignore air resistance on the motion of the cube.
What is the momentum of the cube at point $A$?
$21.9\ m/s$ | |
$24.3\ m/s$ | |
$23.6\ m/s$ | |
$22.2\ m/s$ |
Question 5 Explanation:
[Using $m = 2\ kg, g = 10\ m/s^2, $ $ h_1 = 10\ m$ and $h_2 = 4\ m$]
Kinetic energy at point $A = mg(h_1-h_2 ) = 120\ J$
So, speed at point A
$= v = \sqrt{\dfrac{2KE}{m}} $ $ = \sqrt{\dfrac{2×120}{2}} = 10.95\ m/s$
Momentum at point A
$= mv = 2×10.95 $ $ = 21.9\ m/s$
Kinetic energy at point $A = mg(h_1-h_2 ) = 120\ J$
So, speed at point A
$= v = \sqrt{\dfrac{2KE}{m}} $ $ = \sqrt{\dfrac{2×120}{2}} = 10.95\ m/s$
Momentum at point A
$= mv = 2×10.95 $ $ = 21.9\ m/s$
Question 6 |
A cube of mass $2 \ kg$ is at the top of a twisting road, as shown below.

Bill gently pushes the cube into motion so that it travels the entire path. Ignore air resistance on the motion of the cube.
Point B coincides with the highest point of the projectile motion (of cube) after it leaves point A. What should be the value of $h$?
$9.12\ m$ | |
$7.20\ m$ | |
$7.89\ m$ | |
$8.49\ m$ |
Question 6 Explanation:
After leaving point A, the cube follows projectile motion
And,
$h_{max} = h_A+\dfrac{u_y^2}{2g}$ (where $u_y = u \sin60°$ and $h_A = 4\ m$)
$h_{max} = 4+\dfrac{10.95^2 × \sin^260°}{2 × 10}$
$h_{max} = 8.49\ m $
And,
$h_{max} = h_A+\dfrac{u_y^2}{2g}$ (where $u_y = u \sin60°$ and $h_A = 4\ m$)
$h_{max} = 4+\dfrac{10.95^2 × \sin^260°}{2 × 10}$
$h_{max} = 8.49\ m $
Question 7 |
A cube of mass $2\ kg$ is at the top of a twisting road, as shown below.

Bill gently pushes the cube into motion so that it travels the entire path. Ignore air resistance on the motion of the cube.
In which direction does the law of conservation of linear momentum hold when the cube is traveling from A to B? (Using standard cartesian coordinate system.)
Along the $y$-axis | |
Along the $x$-axis | |
Along the $x$-axis and $y$-axis | |
Neither $x$-axis nor $y$-axis |
Question 7 Explanation:
When the cube travels from A to B, the only force acting on the cube is gravity (downwards).
Thus, momentum of the cube changes along the $y$-axis.
While it stays the same along the $x$-axis.
Thus, momentum of the cube changes along the $y$-axis.
While it stays the same along the $x$-axis.
Question 8 |
Steve is standing in a small boat.
He jumps into the lake with a horizontal velocity of $3\ m/s$ to the left. The boat recoils with a finite velocity towards the right. Which of the below reasons best describes the phenomena?
Choose two correct options:
The boat recoils because of the force applied by Steve | |
The boat recoils because of the law of conservation of momentum | |
The boat recoils because water is not a rigid medium | |
The boat must have recoiled because of external forces like wind |
Question 8 Explanation:
The system consisting of Steve and the boat have no horizontal forces acting on them so their combined momentum is conserved.
Option B → correct
Steve is able to jump out because of the force applied by the boat while the boat moves because of the force applied by Steve.
Option A → correct
Option B → correct
Steve is able to jump out because of the force applied by the boat while the boat moves because of the force applied by Steve.
Option A → correct
Question 9 |
Two balls approach each other from a large distance with equal and opposite momentum. They collide with each other after some time. The two balls scatter in different directions. How does the center of mass of the system change after the collision?
Decelerates, changes direction and accelerates in the new direction | |
Accelerates in the same direction before and after collision | |
Does not change with time | |
Information is insufficient to describe the motion of the center of mass |
Question 9 Explanation:
The two balls form an isolated system with no external forces acting on them.
Thus, the center of mass of the system should not change with time irrespective of the motion of the constituent objects of the system.
Thus, the center of mass of the system should not change with time irrespective of the motion of the constituent objects of the system.
Question 10 |
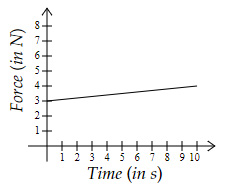
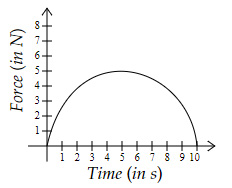
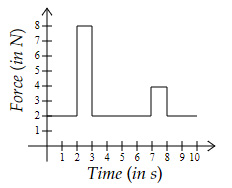
Which graph shows a momentum change of $28\ Ns$?
 | |
 | |
 | |
 |
Question 10 Explanation:
Area under the curve is equal to the impulse (or momentum change).
Option A → $0.5×(3+4)×10 $ $ = 35\ Ns$
Option B → $0.5×(3+4)×4 $ $ +0.5×4×6 $ $ = 26\ Ns$
Option C → $0.5×π×5^2 = 39.2\ Ns$
Option D → $2×2+8×1+2×4 $ $ +1×4+2×2 $ $ = 28\ Ns$
Option A → $0.5×(3+4)×10 $ $ = 35\ Ns$
Option B → $0.5×(3+4)×4 $ $ +0.5×4×6 $ $ = 26\ Ns$
Option C → $0.5×π×5^2 = 39.2\ Ns$
Option D → $2×2+8×1+2×4 $ $ +1×4+2×2 $ $ = 28\ Ns$
Question 11 |
Look at the below figure.
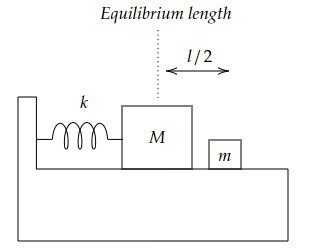
A block of mass $M$ compresses the spring by length $l$. When released, it collides with another block of mass $m$. What is the velocity of the small block after the collision? (Assume the larger block gives up 40% of its momentum to the smaller block.)
$ \dfrac{1}{5} \dfrac{\sqrt{3kl^2 M}}{m}$ | |
$ \dfrac{1}{5} \dfrac{\sqrt{3kl^2 m}}{M}$ | |
$ \dfrac{1}{5} \dfrac{\sqrt{2kl^2 M}}{m}$ | |
$ \dfrac{1}{8} \dfrac{\sqrt{6kl^2 m}}{M}$ |
Question 11 Explanation:
Energy of the system before collision
$= \dfrac{1}{2} kl^2$
Kinetic energy of $M$ before collision
$= \dfrac{1}{2} kl^2-\dfrac{1}{8} kl^2 = \dfrac{3}{8} kl^2$
Using $KE = \dfrac{p^2}{2m}$
Momentum of $M$ before collision
$= \sqrt{2KE×M} $ $ = \sqrt{\dfrac{3}{4} kl^2 M}$
Momentum of $m$ after collision
$= 40\%$ of $\sqrt{\dfrac{3}{4} kl^2 M} $ $ = \dfrac{1}{5} \sqrt{3kl^2 M}$
Thus, velocity of $m$ after collision
$= \dfrac{1}{5} \dfrac{\sqrt{3kl^2 M}}{m}$
$= \dfrac{1}{2} kl^2$
Kinetic energy of $M$ before collision
$= \dfrac{1}{2} kl^2-\dfrac{1}{8} kl^2 = \dfrac{3}{8} kl^2$
Using $KE = \dfrac{p^2}{2m}$
Momentum of $M$ before collision
$= \sqrt{2KE×M} $ $ = \sqrt{\dfrac{3}{4} kl^2 M}$
Momentum of $m$ after collision
$= 40\%$ of $\sqrt{\dfrac{3}{4} kl^2 M} $ $ = \dfrac{1}{5} \sqrt{3kl^2 M}$
Thus, velocity of $m$ after collision
$= \dfrac{1}{5} \dfrac{\sqrt{3kl^2 M}}{m}$
Question 12 |
Two identical objects move with velocities of $2\ m/s \ $ and $- 3\ m/s$, respectively. They undergo a head-on collision (collision in 1D). Which of the below options represents their velocities after the collision?
$-1\ m/s \,$ and $ \, 1\ m/s$ | |
$- 2\ m/s \,$ and $ \, 3\ m/s$ | |
$-4\ m/s \,$ and $ \, 3\ m/s$ | |
$-2\ m/s \,$ and $ \, 1\ m/s$ |
Question 12 Explanation:
If $M$ is the mass of each object,
Total momentum before the collision
$= M(2-3) = -M$
If their final velocities are $u_1\ and\ u_2$
Total momentum after the collision
$= M(u_1+u_2)$
$→ u_1+u_2 = -1$
Final kinetic energy sum ≤ Initial kinetic energy sum
Final kinetic energy sum
$≤ 0.5\ M(4+9) = 6.5\ M$
Check each option,
Option A → Sum of velocities $= -1+1 = 0$ (not allowed)
Option B → Sum of velocities $= -2+3 = 1$ (not allowed)
Option C → $KE = 12.5\ M$ (not allowed)
Option D → Satisfies both the conditions (allowed)
Total momentum before the collision
$= M(2-3) = -M$
If their final velocities are $u_1\ and\ u_2$
Total momentum after the collision
$= M(u_1+u_2)$
$→ u_1+u_2 = -1$
Final kinetic energy sum ≤ Initial kinetic energy sum
Final kinetic energy sum
$≤ 0.5\ M(4+9) = 6.5\ M$
Check each option,
Option A → Sum of velocities $= -1+1 = 0$ (not allowed)
Option B → Sum of velocities $= -2+3 = 1$ (not allowed)
Option C → $KE = 12.5\ M$ (not allowed)
Option D → Satisfies both the conditions (allowed)
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 12 questions to complete.
|
List |
Next Practice Test:
Unit 6: Simple Harmonic Motion >>
AP Physics 1 Main Menu >>
