Our AP Physics 1 practice test on dynamics covers the concept of force and the three laws of motion. As an application of these concepts, some of these problems are based on the concept of free-body diagrams. Two special cases, friction and central forces, are also included.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
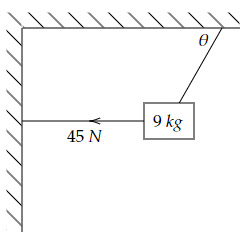
Question 1 |
56.5° | |
58.0° | |
67.2° | |
63.4° |
Question 1 Explanation:
The Free Body Diagram of the block is,
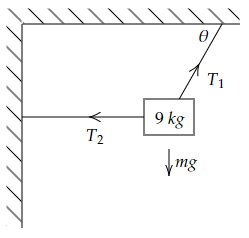
Sum of Vertical Forces
$= T_1 \sinθ-mg $ $ = 0 → T_1 \sinθ = mg$
Sum of Horizontal Forces
$= T_1 \cosθ-T_2 $ $ = 0 → T_1 \cosθ = T_2$
$\tanθ = \dfrac{mg}{T_2}$
Using $m = 9\ kg, T_2 = 45\ N $ and $g = 10\ m/s^2,$
$\tanθ = 2$
$→ θ = 63.4°$

Sum of Vertical Forces
$= T_1 \sinθ-mg $ $ = 0 → T_1 \sinθ = mg$
Sum of Horizontal Forces
$= T_1 \cosθ-T_2 $ $ = 0 → T_1 \cosθ = T_2$
$\tanθ = \dfrac{mg}{T_2}$
Using $m = 9\ kg, T_2 = 45\ N $ and $g = 10\ m/s^2,$
$\tanθ = 2$
$→ θ = 63.4°$
Question 2 |
Two blocks are at rest over a rough surface whose coefficient of friction $μ_s$ is $0.3$.
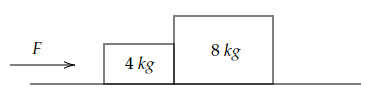
The minimum force $F$ needed to set the system of blocks in motion is,
$30\ N$ | |
$33\ N$ | |
$36\ N$ | |
$39\ N$ |
Question 2 Explanation:
The Free Body Diagram of the system of blocks is,
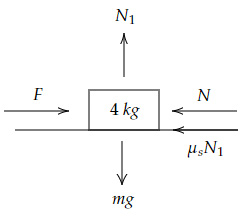
Sum of vertical forces
$= N_1- mg = 0 → N_1 = mg$
Sum of horizontal forces
$= F- N-μ_s mg $ $ = 0 → F $ $ = N+μ_s mg …(1)$ And,
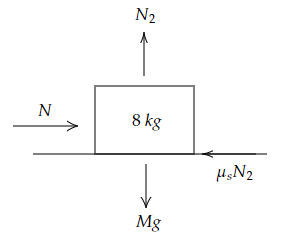
Sum of vertical forces
$= N_2-Mg = 0 → N_2 = Mg$
Sum of horizontal forces
$= N-μ_s Mg $ $ = 0 → N = μ_s Mg …(2)$
Using (1) and (2),
$F = μ_s g(M+m)$
Using $m = 4\ kg, M = 8\ kg, μ_s = 0.3$ and $g = 10\ m/s^2$
$F = 0.3×10×(4+8)$
$F = 36\ N$

Sum of vertical forces
$= N_1- mg = 0 → N_1 = mg$
Sum of horizontal forces
$= F- N-μ_s mg $ $ = 0 → F $ $ = N+μ_s mg …(1)$ And,

Sum of vertical forces
$= N_2-Mg = 0 → N_2 = Mg$
Sum of horizontal forces
$= N-μ_s Mg $ $ = 0 → N = μ_s Mg …(2)$
Using (1) and (2),
$F = μ_s g(M+m)$
Using $m = 4\ kg, M = 8\ kg, μ_s = 0.3$ and $g = 10\ m/s^2$
$F = 0.3×10×(4+8)$
$F = 36\ N$
Question 3 |
Calculate the average force acting on a block of mass $6.2\ kg$ if it accelerates from rest to $28\ m/s$ in $5.2 \ s$.
$38.2\ N$ | |
$45.3\ N$ | |
$28.8\ N$ | |
$33.4\ N$ |
Question 3 Explanation:
Average acceleration $= \dfrac{28-0}{5.2} = 5.4\ m/s^2$
Average force $= 6.2×5.4 = 33.4\ N$
Average force $= 6.2×5.4 = 33.4\ N$
Question 4 |
A ball of mass $2\ kg$ is initially at rest at the top of a smooth spherical surface of radius $5\ cm$. It is gently pushed so that it starts moving. After rolling through an angle $θ$ it loses contact with the surface.
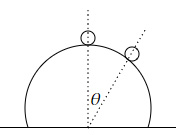
What is the contact force when the ball loses contact with the surface?
$0\ N$, because the two surfaces are no longer in contact | |
$1.6\ N$, because the contact force is causing centripetal acceleration | |
$0\ N$, because the gravity can provide sufficient centripetal force | |
Cannot be determined, because the nature of the surfaces is not known |
Question 4 Explanation:
Contact force in this case is the normal force and when the two surfaces are no longer in contact the normal force must be zero.
Question 5 |
An object of mass $2\ kg$ starts sliding on a rough incline. The coefficient of kinetic friction between the mass and the incline is $0.22$. The incline is $10\ m$ long. How much less time does the object take to reach the bottom of the incline if there is no friction? (Take the angle of the incline with the horizontal as $30°$)
$0.47\ s$ | |
$0.54\ s$ | |
$0.11\ s$ | |
$0.27\ s$ |
Question 5 Explanation:
Free body diagram of the mass is,
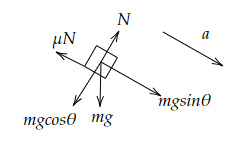
Sum of forces along the direction of $N$
$= N-mg \cosθ $ $ = 0 → N = mg \cosθ$
Sum of forces along the direction of $a$
$mg \sinθ-μN $ $ = ma → mg \sinθ-μmg \cosθ $ $ = ma$
$g(\sinθ-μ \cosθ ) = a$
Using $θ = 30°, g = 10\ m/s^2 $ and $ μ = 0.22$
For rough incline, $a = 3.09\ m/s^2$
For smooth incline, $a = 5.00\ m/s^2$
$s = \dfrac{1}{2} at^2$ for an object starting from rest $(\text{Here}\ s = 10\ m)$
Time taken to reach the bottom of the rough incline
$= \sqrt{\dfrac{2s}{a}} = 2.54\ s$
Time taken to reach the bottom of the smooth incline
$\sqrt{\dfrac{2s}{a}} = 2\ s$
Time difference $= 2.54-2 = 0.54\ s$

Sum of forces along the direction of $N$
$= N-mg \cosθ $ $ = 0 → N = mg \cosθ$
Sum of forces along the direction of $a$
$mg \sinθ-μN $ $ = ma → mg \sinθ-μmg \cosθ $ $ = ma$
$g(\sinθ-μ \cosθ ) = a$
Using $θ = 30°, g = 10\ m/s^2 $ and $ μ = 0.22$
For rough incline, $a = 3.09\ m/s^2$
For smooth incline, $a = 5.00\ m/s^2$
$s = \dfrac{1}{2} at^2$ for an object starting from rest $(\text{Here}\ s = 10\ m)$
Time taken to reach the bottom of the rough incline
$= \sqrt{\dfrac{2s}{a}} = 2.54\ s$
Time taken to reach the bottom of the smooth incline
$\sqrt{\dfrac{2s}{a}} = 2\ s$
Time difference $= 2.54-2 = 0.54\ s$
Question 6 |
$A$ variable force $F$ acts on an object according to time $T$, as shown below.
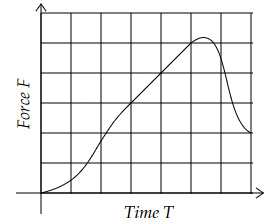
The velocity of the object,
(Choose two correct answers.)
Depends on the mass of the object | |
Increases and then decreases over time | |
Keeps on increases over time | |
Increases linearly for some time between the initial and final times |
Question 6 Explanation:
Acceleration depends on the force applied which are related with each other through mass and thus the velocity of the object depends on the mass of the object.
→ Option A is true
The force on the object is always positive thus,
The acceleration of the object is always positive thus,
The velocity of the object must constantly increase over time.
→ Option C is true
→ Option A is true
The force on the object is always positive thus,
The acceleration of the object is always positive thus,
The velocity of the object must constantly increase over time.
→ Option C is true
Question 7 |
Look at the below spring-mass system. The springs are identical in length and nature.
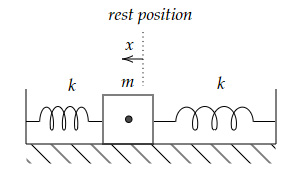
What is the net acceleration of the mass when it is displaced slightly from the rest position by $x$?
$\dfrac{2kx}{m}$ | |
$\dfrac{kx}{m}$ | |
$0$ | |
$\dfrac{4kx}{m}$ |
Question 7 Explanation:
Sum of horizontal forces $= kx+kx = ma$
$2kx = ma$
$a = \dfrac{2kx}{m}$
$2kx = ma$
$a = \dfrac{2kx}{m}$
Question 8 |
Sally needs to verify the statements given by Nancy regarding the below graph. Which of the options should Sally mark as correct?
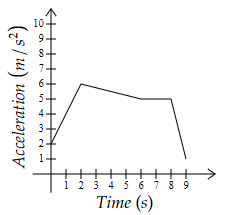
Choose two correct answers:
The net force acting on the object from $8 \ s$ to $9 \ s$ is $0\ N$ | |
The velocity increases as $n^{th}$ power of time $t$ from $0\ s$ to $2\ s$ where $n > 1$ | |
The velocity change from $2\ s$ to $6\ s$ is equal to $20\ m/s$ | |
The net force acting on the object from $6\ s$ to $8\ s$ is constant |
Question 8 Explanation:
Acceleration decreases from $8\ s$ to $9\ s$.
Option A → False
Acceleration increases linearly from $0\ s$ to $2\ s$
Thus, velocity should increase as $2^{nd}$ power of time $(v-u = at)$.
Option B → True
Velocity change is equal to the area below the curve.
Area $= \dfrac{1}{2}×(6+5)×4 $ $ = 22\ m/s$
Option C → False
Force is proportional to the acceleration of the object.
Option D → True
Option A → False
Acceleration increases linearly from $0\ s$ to $2\ s$
Thus, velocity should increase as $2^{nd}$ power of time $(v-u = at)$.
Option B → True
Velocity change is equal to the area below the curve.
Area $= \dfrac{1}{2}×(6+5)×4 $ $ = 22\ m/s$
Option C → False
Force is proportional to the acceleration of the object.
Option D → True
Question 9 |
What is the apparent weight of a block of mass $m$, going up in an elevator with an acceleration $a$?
$m(g-2a)$ | |
$2m(g-a)$ | |
$m(g+a)$ | |
$\dfrac{1}{2} ma$ |
Question 9 Explanation:
Sum of vertical forces $= N-mg = ma$
$N = m(g+a)$
An object feels its weight due to the normal force acting from the other object.
Thus, apparent weight $= m(g+a)$
$N = m(g+a)$
An object feels its weight due to the normal force acting from the other object.
Thus, apparent weight $= m(g+a)$
Question 10 |
Questions 10, 11 and 12 are based on the below information.
Two blocks, kept on a smooth incline plane, are connected by a massless string going over a pulley, as shown below.
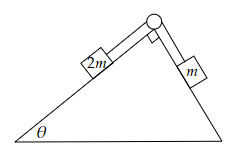
If the two blocks are at rest, then which of the below relations must be correct?
$\cotθ = 0.5$ | |
$\tanθ = 0.5$ | |
$\secθ = 2.5$ | |
$\tanθ = \sqrt2$ |
Question 10 Explanation:
Sum of forces along the incline on $2m$
$= T-2mg\; \sinθ = 0 → T $ $ = 2mg\; \sinθ$
Sum of forces along the incline on $m$
$= T-mg\; \sin(90-θ) $ $ = 0 → T = mg\; \cosθ$
$→ 2 \tanθ = 1\ $ OR $\ \tanθ = 0.5$
$= T-2mg\; \sinθ = 0 → T $ $ = 2mg\; \sinθ$
Sum of forces along the incline on $m$
$= T-mg\; \sin(90-θ) $ $ = 0 → T = mg\; \cosθ$
$→ 2 \tanθ = 1\ $ OR $\ \tanθ = 0.5$
Question 11 |
Two blocks, kept on a smooth incline plane, are connected by a massless string going over a pulley, as shown below.

If the actual $θ = 20°$, then what will be the acceleration of the lighter block?
$0.08g,$ $\text{down the incline}$ | |
$0.12g,$ $\text{up the incline}$ | |
$0.18g,$ $\text{up the incline}$ | |
$0.15g,$ $\text{down the incline}$ |
Question 11 Explanation:
{Assume a certain direction of acceleration for calculation if answer is negative the actual direction will be opposite to the assumption.}
Sum of forces along the incline on $m$
$= mg\; \cosθ-T = ma$
(acceleration down the incline)
Sum of forces along the incline on $2m$
$= T-2mg\; \sinθ = 2ma$
(acceleration up the incline)
Adding the two equations,
$mg \cosθ-2mg\; \sinθ = 3ma$
$mg(\cosθ-2 \sinθ ) = 3ma$
Using $θ = 20°$,
$a = \dfrac{g}{3} (0.25)$
$a = 0.08g$
Sum of forces along the incline on $m$
$= mg\; \cosθ-T = ma$
(acceleration down the incline)
Sum of forces along the incline on $2m$
$= T-2mg\; \sinθ = 2ma$
(acceleration up the incline)
Adding the two equations,
$mg \cosθ-2mg\; \sinθ = 3ma$
$mg(\cosθ-2 \sinθ ) = 3ma$
Using $θ = 20°$,
$a = \dfrac{g}{3} (0.25)$
$a = 0.08g$
Question 12 |
Two blocks, kept on a smooth incline plane, are connected by a massless string going over a pulley, as shown below.

Why does the pulley stay in the same place?
The friction force between the pulley and the incline balances the tension forces | |
The gravitational force of the pulley balances the tension forces | |
The normal reaction between the pulley and the incline balances the tension forces | |
Tension forces are of equal strength and so no other force is needed to balance them |
Question 12 Explanation:
The pulley is acted upon by tension forces in different directions.
Thus, the contact (Normal) force balances the tension forces acting on the pulley.
Thus, the contact (Normal) force balances the tension forces acting on the pulley.
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 12 questions to complete.
|
List |
Next Practice Test:
Unit 3: Circular Motion & Gravitation >>
AP Physics 1 Main Menu >>