This free AP Physics 1 practice test covers unit 1, which is kinematics. You will be tested on the concepts of average and instantaneous motion, acceleration, motion under gravity, graphical analysis of motion, and relative motion. As an application of these concepts, you will see projectile motion and uniform circular motion as well.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
A boy throws a disc in the air with a velocity of $11\ m/s$ at an angle of $60^°$ with the horizontal. The initial velocity vector is $\overrightarrow{v_i}$, and the final velocity vector is $\overrightarrow{v_f}$. The difference between the initial and the final velocity vector is equal to,
$19.04 \ m/s$ $\text{(downwards)}$ | |
$15.02 \ m/s$ $\text{(downwards)}$ | |
$11.00 \ m/s$ $\text{(downwards)}$ | |
$20.54 \ m/s$ $\text{(downwards)}$ |
Question 1 Explanation:
For initial velocity $v_i$,
x-component = $11×\cos 60° = 5.50\ m/s$ (right)
y-component = $11×\sin 60° = 9.52\ m/s$ (upwards)
As the disc is in free fall (neglecting air drag) only the vertical component reverses in direction with no change in magnitude when it returns to the same height.
For final velocity $v_f,$
x-component = $5.50\ m/s$ (right)
y-component = $9.52\ m/s$ (downwards)
Difference in velocity = Difference between the $y$ components
Difference in y components $= 9.52-(-9.52) = 19.04\ m/s$ (downwards)
x-component = $11×\cos 60° = 5.50\ m/s$ (right)
y-component = $11×\sin 60° = 9.52\ m/s$ (upwards)
As the disc is in free fall (neglecting air drag) only the vertical component reverses in direction with no change in magnitude when it returns to the same height.
For final velocity $v_f,$
x-component = $5.50\ m/s$ (right)
y-component = $9.52\ m/s$ (downwards)
Difference in velocity = Difference between the $y$ components
Difference in y components $= 9.52-(-9.52) = 19.04\ m/s$ (downwards)
Question 2 |
Look at the below velocity-time graph for an object moving in 1D.
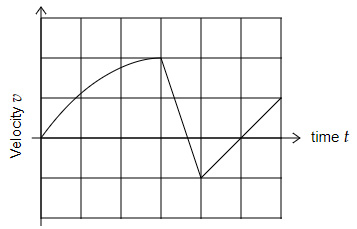
Which of the below statements is TRUE?
Displacement is equal to the distance covered by the object | |
The object reverses its direction three times during its motion | |
The velocity of the object shows abrupt change in acceleration two times | |
The object returns to its starting point at the end of the motion |
Question 2 Explanation:
Net displacement is lesser than the distance covered as the object turns its direction.
Option A → False
The velocity of the object changes its sign twice.
Option B → False
The graph shows two sudden changes in velocity.
Option C → True
The area above the graph is not equal to the area below the graph.
Option D → False
Option A → False
The velocity of the object changes its sign twice.
Option B → False
The graph shows two sudden changes in velocity.
Option C → True
The area above the graph is not equal to the area below the graph.
Option D → False
Question 3 |
A stone is thrown off an incline as shown in the figure.
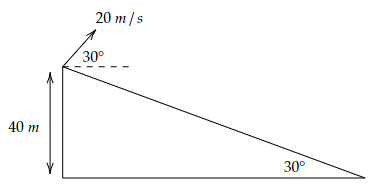
At what height above the incline is the stone when it is again on the same horizontal level as the initial point?
30.6 $m$ | |
28.5 $m$ | |
34.6 $m$ | |
20.1 $m$ |
Question 3 Explanation:
y-component of initial velocity
$= 20×\sin 30^° = 10\ m/s$
Time to reach the highest point on the trajectory
$= \dfrac{10}{10} = 1\ sec\ (Using\ g = 10\ m/s^2)$
Thus, time to reach the same horizontal level
$= 2×1 = 2\ sec$
x-component of initial velocity
$= 20×\cos 30^° = 17.3\ m/s$
Horizontal distance covered
$= 17.3×2 = 34.6\ m$
Using basic trigonometric definitions,
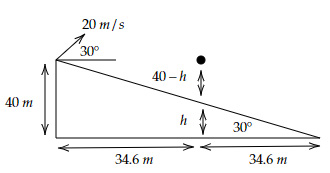
Thus, $h = 34.6×\tan 30^° = 19.9\ m$
Height above the incline
$= 40-h = 40-19.9 = 20.1\ m$
$= 20×\sin 30^° = 10\ m/s$
Time to reach the highest point on the trajectory
$= \dfrac{10}{10} = 1\ sec\ (Using\ g = 10\ m/s^2)$
Thus, time to reach the same horizontal level
$= 2×1 = 2\ sec$
x-component of initial velocity
$= 20×\cos 30^° = 17.3\ m/s$
Horizontal distance covered
$= 17.3×2 = 34.6\ m$
Using basic trigonometric definitions,

Thus, $h = 34.6×\tan 30^° = 19.9\ m$
Height above the incline
$= 40-h = 40-19.9 = 20.1\ m$
Question 4 |
Gary spins an object tied with a thread, as shown below.
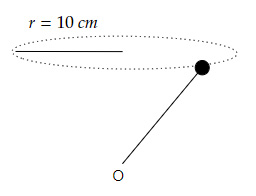
The object completes 10 revolutions per minute.
By what factor does the centripetal acceleration of the object increase when Gary spins the object at 20 revolutions per minute?
3 | |
4 | |
5 | |
6 |
Question 4 Explanation:
Centripetal acceleration $a_c = \dfrac{v^2}{r}$
And, $v = 2πrf → a_c = 4π^2 rf^2$
Ratio of acceleration is,
$\dfrac{ac_2}{ac_1} = \dfrac{f_2^2}{f_1^2 }$
Using $f_1 = 10\ rpm$ and $f_2 = 20\ rpm $
$\dfrac{ac_2 }{ac_1} = \dfrac{20^2}{10^2}$
$\dfrac{ac_2 }{ac_1} = 4$
Thus, acceleration increases by a factor of 4.
And, $v = 2πrf → a_c = 4π^2 rf^2$
Ratio of acceleration is,
$\dfrac{ac_2}{ac_1} = \dfrac{f_2^2}{f_1^2 }$
Using $f_1 = 10\ rpm$ and $f_2 = 20\ rpm $
$\dfrac{ac_2 }{ac_1} = \dfrac{20^2}{10^2}$
$\dfrac{ac_2 }{ac_1} = 4$
Thus, acceleration increases by a factor of 4.
Question 5 |
Let $(x,y)$ denote the coordinates of a projectile starting at the origin of a coordinate system with a speed of $1\ m/s$ and at an angle of $45^°$ with the $x$-axis. Neglecting air drag, the equation satisfied by $x$ and $y$ is of,
Hyperbola, because $x$ and $y$ are dependent on 2nd power of time $t$ | |
Parabola, because $x$ is linearly dependent on time $t$ and $y$ is dependent on the 2nd power of time $t$ | |
Straight line, because $x$ and $y$ are linearly dependent on time $t$ | |
Ellipse, because $x$ and $y$ are coordinates describing a symmetric motion in space |
Question 5 Explanation:
Note,
$x = \dfrac{t}{\sqrt2} \, $ and $ \, y = \dfrac{t}{\sqrt2} - \dfrac{1}{2}\ gt^2$
Thus, $x$ is linearly dependent on $t$ and $y$ is dependent on the 2nd power of $t$. Combining them gives the equation of a parabola:
$y = x-gx^2$
$x = \dfrac{t}{\sqrt2} \, $ and $ \, y = \dfrac{t}{\sqrt2} - \dfrac{1}{2}\ gt^2$
Thus, $x$ is linearly dependent on $t$ and $y$ is dependent on the 2nd power of $t$. Combining them gives the equation of a parabola:
$y = x-gx^2$
Question 6 |
Which of the below velocity-time graphs shows an average acceleration greater than $2\ m/s^2$?
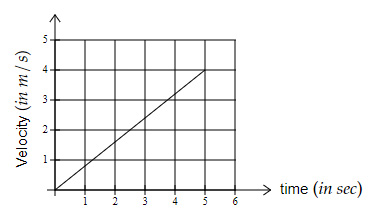 | |
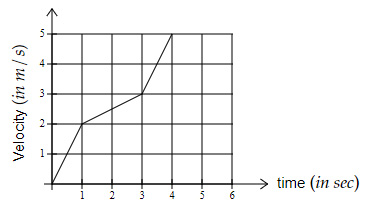 | |
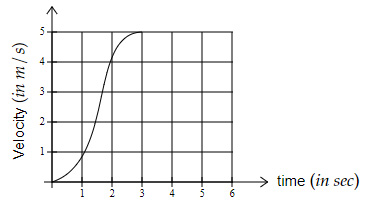 | |
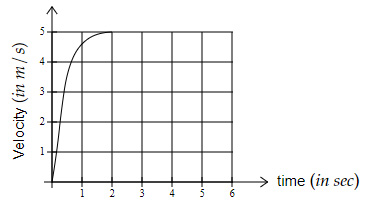 |
Question 6 Explanation:
Using, average acceleration:
$a_{avg} = \dfrac{v_{final} - v_{initial}}{t_{final} - t_{initial}}$
For option $A → \dfrac{4-0}{5-0}=0.8\ m/s^2$
For option $B → \dfrac{5-0}{4-0}=1.25\ m/s^2$
For option $C → \dfrac{5-0}{3-0}=1.67\ m/s^2$
For option $D → \dfrac{5-0}{2-0}=2.5\ m/s^2$ (greater than $2\ m/s^2$)
$a_{avg} = \dfrac{v_{final} - v_{initial}}{t_{final} - t_{initial}}$
For option $A → \dfrac{4-0}{5-0}=0.8\ m/s^2$
For option $B → \dfrac{5-0}{4-0}=1.25\ m/s^2$
For option $C → \dfrac{5-0}{3-0}=1.67\ m/s^2$
For option $D → \dfrac{5-0}{2-0}=2.5\ m/s^2$ (greater than $2\ m/s^2$)
Question 7 |
If the average acceleration of a particle is $0\ m/s^2$, then which of the below conclusions is false?
The particle returned to its initial velocity after some time | |
The displacement of the particle may or may not be zero | |
The particle can have uniform velocity for the entire time interval | |
The instantaneous acceleration of the particle anytime within the time interval must be zero |
Question 7 Explanation:
For zero average acceleration, initial and final velocity must be equal.
Option A → True
Zero average acceleration implies particle is at rest or moving with uniform velocity So, displacement of the particle may or may not be zero.
Option B → True
Option C → True
Instantaneous acceleration does not depend upon average acceleration and in general can vary taking either positive or negative values.
Option D → False
Option A → True
Zero average acceleration implies particle is at rest or moving with uniform velocity So, displacement of the particle may or may not be zero.
Option B → True
Option C → True
Instantaneous acceleration does not depend upon average acceleration and in general can vary taking either positive or negative values.
Option D → False
Question 8 |
Alexa throws two stones, who is standing on a building of height $10\ m$. She throws the 1st stone upward with a velocity of $10\ m/s$ and the 2nd stone to the right with a speed of $20\ m/s$. Which stone will have a greater vertical component of the velocity when they reach the ground? (Assume that the mass of the 1st stone is greater than the mass of the 2nd stone.)
2nd Stone because it will reach the ground earlier | |
1st Stone because it is heavier | |
1st Stone because it has non-zero initial velocity (in vertical direction) | |
2nd Stone because it has higher initial velocity than the 1st stone |
Question 8 Explanation:
Velocity of stone 1 when it passes through its initial point (in the downward direction) has a velocity of $10\ m/s$ while velocity of stone 2 is $20\ m/s$ going towards the right. (So, it has 0 initial velocity in the vertical direction.)
Thus, stone 1 will have a greater vertical component for the final velocity when it reaches the ground.
Thus, stone 1 will have a greater vertical component for the final velocity when it reaches the ground.
Question 9 |
Questions 9 and 10 are based on the below information.
A bicycle moves along a straight path according to the graph shown below.
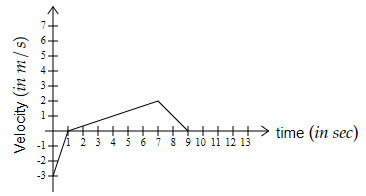
Why is the distance covered by the bicycle greater than the displacement?
The statement is always true irrespective of the motion of the bicycle | |
The bicycle reversed its direction so the effective displacement is lesser | |
The bicycle decelerated from 7 to 9 seconds so the displacement decreased | |
The question is incorrect, the area between the curve and the $x-axis$ is always positive so the displacement and the distance must be the same |
Question 9 Explanation:
The bicycle reversed its direction at $t = 1\ s$, hence the displacement covered is lesser while the distance covered is more.
Question 10 |
A bicycle moves along a straight path according to the graph shown below.

Which of the below graphs shows the acceleration of the bicycle?
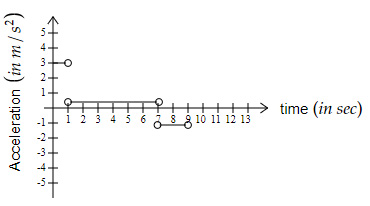 | |
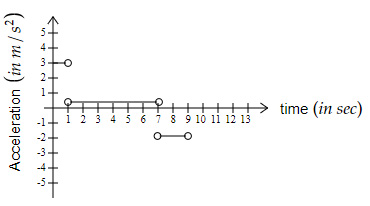 | |
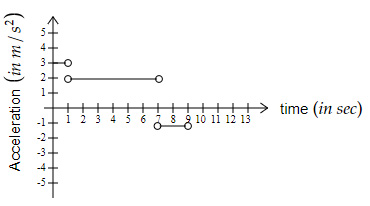 | |
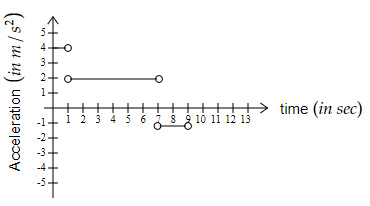 |
Question 10 Explanation:
Acceleration from
$t = 0 \ s \ $ to $ \ 1 \ s \ $ is: $ \ a = \dfrac{0-(-3)}{1-0} = 3\ m/s^2$
Acceleration from
$t = 1 \ s \ $ to $ \ 7 \ s \ $is: $\ a = \dfrac{2-0}{7-1} = 0.33\ m/s^2$
Acceleration from
$t = 7 \ s \ $ to $ \ 9 \ s \ $ is: $ \ a = \dfrac{0-2}{9-7} = -1\ m/s^2$
When plotted, the graph should be as shown in option A.
$t = 0 \ s \ $ to $ \ 1 \ s \ $ is: $ \ a = \dfrac{0-(-3)}{1-0} = 3\ m/s^2$
Acceleration from
$t = 1 \ s \ $ to $ \ 7 \ s \ $is: $\ a = \dfrac{2-0}{7-1} = 0.33\ m/s^2$
Acceleration from
$t = 7 \ s \ $ to $ \ 9 \ s \ $ is: $ \ a = \dfrac{0-2}{9-7} = -1\ m/s^2$
When plotted, the graph should be as shown in option A.
Question 11 |
A particle is performing uniform circular motion of radius $2\ cm$ and frequency of $7\ rps$. Which of the below quantities show the correct description of the motion?
Choose two correct answers:
$\text{Velocity }$ $v = 0.87\ m/s$ | |
$\text{Acceleration }$ $a = 12.5\ m/s^2$ | |
$\text{Time Period }$ $t = 0.26\ s$ | |
$\text{Angular velocity }$ $ω = 43.9\ rad/s$ |
Question 11 Explanation:
$r = 2\ cm$ and $f = 7\ rps$
$T = \dfrac{1}{f} = 0.14\ s$ (Option C is False)
$ω = 2πf = 2×π×7 $ $ = 43.9\ rad/s$ (Option D is True)
$v = \dfrac{2πr}{T} = \dfrac{2×π×0.02}{0.14} $ $ = 0.89\ m/s$ (Option A is True)
$a = \dfrac{v^2}{r} = \dfrac{0.89^2}{0.02} $ $ = 39.6\ m/s^2$ (Option B is False)
$T = \dfrac{1}{f} = 0.14\ s$ (Option C is False)
$ω = 2πf = 2×π×7 $ $ = 43.9\ rad/s$ (Option D is True)
$v = \dfrac{2πr}{T} = \dfrac{2×π×0.02}{0.14} $ $ = 0.89\ m/s$ (Option A is True)
$a = \dfrac{v^2}{r} = \dfrac{0.89^2}{0.02} $ $ = 39.6\ m/s^2$ (Option B is False)
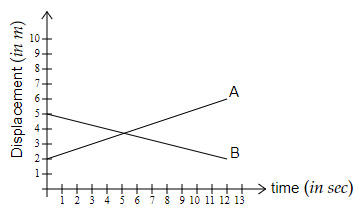
Question 12 |
$\dfrac{1}{12}\;m/s$ | |
$-\dfrac{3}{5}\;m/s$ | |
$\dfrac{7}{12}\;m/s$ | |
$\dfrac{3}{4}\;m/s$ |
Question 12 Explanation:
Velocity of $A = \dfrac{6 - 2}{12 - 0} = \dfrac{1}{3}\;m/s$
Velocity of $B = \dfrac{2 - 5}{12 - 0} = -\dfrac{1}{4}\; m/s$
Velocity of $A$ as seen by $B = \dfrac{1}{3}-(-\dfrac{1}{4}) $ $ = \dfrac{7}{12}\;m/s$
Velocity of $B = \dfrac{2 - 5}{12 - 0} = -\dfrac{1}{4}\; m/s$
Velocity of $A$ as seen by $B = \dfrac{1}{3}-(-\dfrac{1}{4}) $ $ = \dfrac{7}{12}\;m/s$
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 12 questions to complete.
|
List |
Next Practice Test:
Unit 2: Dynamics >>
AP Physics 1 Main Menu >>