Our free AP Physics 1, Unit 7 test covers the concepts of parallel moments, torque, and rotational equilibrium. Additional topics include kinematics of rotational motion, moment of inertia, and angular momentum. Learning all of these concepts will ensure that you are fully prepared for your Physics 1 exam.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
Two boxes of mass $10\ kg$ and $18\ kg$ are on either side of the pivot, as shown below.
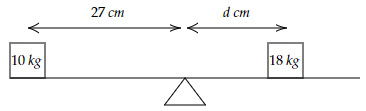
At what distance $d$ should the $18\ kg$ mass be kept so that the two sides are balanced about the pivot?
$10\ cm$ | |
$15\ cm$ | |
$12\ cm$ | |
$18\ cm$ |
Question 1 Explanation:
For equilibrium, torque on either side must be the same,
$10×27×g = 18×d×g$
$d = 15 \ cm$
$10×27×g = 18×d×g$
$d = 15 \ cm$
Question 2 |
A ladder of mass $5\ kg$ is resting on a frictionless wall. However, the friction between the foot of the ladder and the floor is non-zero.
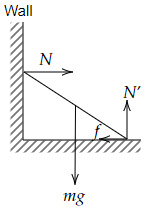
What is the normal force acting on the ladder due to the wall? (Hint: Consider the foot of the ladder as a pivot.)
$25\sqrt{3} N$ | |
$23\sqrt{2} N$ | |
$20\sqrt{5} N$ | |
$25\sqrt{6} N$ |
Question 2 Explanation:
Free body diagram of the ladder is,
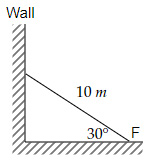
Torque about the pivot
$= 10×N×\sin 150°-5×5×10×\sin 120°$
$= 10N \sin 30°-250\ \sin 60°$
$= 5N-125 \sqrt{3}$
$= 0$
Thus, $N = 25\sqrt{3}\ N$

Torque about the pivot
$= 10×N×\sin 150°-5×5×10×\sin 120°$
$= 10N \sin 30°-250\ \sin 60°$
$= 5N-125 \sqrt{3}$
$= 0$
Thus, $N = 25\sqrt{3}\ N$
Question 3 |
A cylindrical object is fixed about a line passing through its axis. It is set into motion by applying a torque. The angular velocity of the cylinder increases to $0.8\ rad/s$ in $2\ s$. If the moment of inertia of the cylinder is equal to $4\ kgm^2$, what is the average torque acting on the cylinder?
$2.7\ Nm$ | |
$4.3\ Nm$ | |
$3.6\ Nm$ | |
$1.6\ Nm$ |
Question 3 Explanation:
Average angular acceleration
$α = \dfrac{0.8-0}{2} $ $ = 0.4\ rad/s^2$
Average torque
$= Iα = 4×0.4 $ $ = 1.6\ Nm$
$α = \dfrac{0.8-0}{2} $ $ = 0.4\ rad/s^2$
Average torque
$= Iα = 4×0.4 $ $ = 1.6\ Nm$
Question 4 |
A massless spring joining two identical blocks is rotating, as shown below.
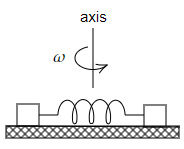
If Max increases the angular velocity of the system, which of the below statements is TRUE?
The moment of inertia of the system increases | |
The moment of inertia of the system decreases | |
The moment of inertia of the system does not change | |
The moment of inertia of the system may change depending upon other factors |
Question 4 Explanation:
Max increases the angular velocity of the system
$→ T_{ext} ≠ 0$
As the system is performing rotational motion,
$a_c = rω^2$
As $ω$ increases $a_c$ or the centripetal force must increase which in this case is the spring force, and for spring force to increase the spring must elongate as,
$I = ∑mr^2$
Implies the moment of inertia must increase.
$→ T_{ext} ≠ 0$
As the system is performing rotational motion,
$a_c = rω^2$
As $ω$ increases $a_c$ or the centripetal force must increase which in this case is the spring force, and for spring force to increase the spring must elongate as,
$I = ∑mr^2$
Implies the moment of inertia must increase.
Question 5 |
A disk with a moment of inertia $\frac{MR^2}{2}$ is rotating with an angular velocity of $ω_o$. It slows down due to frictional forces between the disk and the axle. If the disk rotates $N$ times before stopping completely, what is the magnitude of the frictional torque acting on the disk?
$\dfrac{MR^2 ω_o^2}{16πN}$ | |
$\dfrac{MR^2 ω_o^2}{4πN}$ | |
$\dfrac{MR^2 ω_o^2}{8πN}$ | |
$\dfrac{MR^2 ω_o^2}{8N}$ |
Question 5 Explanation:
Angle turned $Δθ = 2πN$
$ω^2 = ω_o^2+2αΔθ$
[Using $ω = 0, Δθ = 2πN$]
$0 = ω_o^2+4πNα$
Or $\ α = -\dfrac{ω_o^2}{4πN}$
Torque $= Iα = \dfrac{MR^2 ω_o^2}{8πN}$
(Neglecting the – sign as we only need the magnitude.)
$ω^2 = ω_o^2+2αΔθ$
[Using $ω = 0, Δθ = 2πN$]
$0 = ω_o^2+4πNα$
Or $\ α = -\dfrac{ω_o^2}{4πN}$
Torque $= Iα = \dfrac{MR^2 ω_o^2}{8πN}$
(Neglecting the – sign as we only need the magnitude.)
Question 6 |
Questions 6 and 7 are based on the below information.
A thin stick of length $30\ cm$ is made to rotate either about point $X$ or $Y$. The forces acting on the stick are as follows.
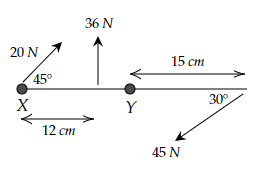
What is the net torque acting on the stick about an axis passing through $X$?
$4.37\ Nm$ | |
$2.43\ Nm$ | |
$6.18\ Nm$ | |
$3.13\ Nm$ |
Question 6 Explanation:
[Note: Clockwise torques are considered positive and anticlockwise torques are considered negative.]
Total torque about $X$:
$= 20×0-36×\dfrac{12}{100}+\dfrac{30}{100}×45×\sin150°$
$=0 -36×0.12+0.30×45×\sin30°$
$= 2.43\ Nm$
Total torque about $X$:
$= 20×0-36×\dfrac{12}{100}+\dfrac{30}{100}×45×\sin150°$
$=0 -36×0.12+0.30×45×\sin30°$
$= 2.43\ Nm$
Question 7 |
A thin stick of length $30\ cm$ is made to rotate either about point $X$ or $Y$. The forces acting on the stick are as follows.

How much is the net torque acting on the stick for an axis passing through $Y$?
$4.32\ Nm$ | |
$9.13\ Nm$ | |
$8.21\ Nm$ | |
$6.57\ Nm$ |
Question 7 Explanation:
Total torque about $Y$:
$\dfrac{15}{100}×20×\sin135°+36×\dfrac{3}{100}+\dfrac{15}{100}$ $ ×45×\sin150°$
$= 0.15×20×\sin45°$$+ \, 36×0.03+0.15 $ $ × \, 45×\sin30°$
$= 6.57 Nm$
$\dfrac{15}{100}×20×\sin135°+36×\dfrac{3}{100}+\dfrac{15}{100}$ $ ×45×\sin150°$
$= 0.15×20×\sin45°$$+ \, 36×0.03+0.15 $ $ × \, 45×\sin30°$
$= 6.57 Nm$
Question 8 |
A sphere made of clay is rotating about an axis passing through its center. Due to internal forces, the clay distorts into an oval-shaped object with a moment of inertia $20\%$ more than the initial moment of inertia. By what percentage does the angular speed of the clay change?
$17%$ | |
$25%$ | |
$32%$ | |
$49%$ |
Question 8 Explanation:
Assume, initial moment of inertia $= I_o$
and initial angular speed $= ω_o$
$I_1 = I_o+0.2I_o = 1.2I_o$
As no external torques are acting on the clay,
$I_o ω_o = I_1 ω_1$
Thus, $ω_1 = \dfrac{I_o ω_o}{I_1} = \dfrac{1}{1.2} ω_o $ $ = 0.83ω_o$
$\%$ decrease in $ω_o = \dfrac{ω_o-0.83ω_o}{ω_o} ×100 $ $ = 17% $
and initial angular speed $= ω_o$
$I_1 = I_o+0.2I_o = 1.2I_o$
As no external torques are acting on the clay,
$I_o ω_o = I_1 ω_1$
Thus, $ω_1 = \dfrac{I_o ω_o}{I_1} = \dfrac{1}{1.2} ω_o $ $ = 0.83ω_o$
$\%$ decrease in $ω_o = \dfrac{ω_o-0.83ω_o}{ω_o} ×100 $ $ = 17% $
Question 9 |
Find the velocity of a sphere of radius $R$ and mass $M$ at the bottom of the plane if it starts rolling without slipping on an inclined plane from height $h$.

(Note the moment of inertia of a sphere is $\frac{2}{5} MR^2$.)
$\sqrt{\dfrac{4gh}{3}}$ | |
$\sqrt{\dfrac{11gh}{8}}$ | |
$\sqrt{\dfrac{5gh}{2}}$ | |
$\sqrt{\dfrac{10gh}{7}}$ |
Question 9 Explanation:
Initial potential energy = $Mgh$
Total kinetic energy = $\dfrac{1}{2} Mv^2+\dfrac{1}{2} Iω^2$
For rolling without slipping,
$v = ωR \, $ and $ \, I_{sphere} = \dfrac{2}{5} MR^2$
Thus, Total kinetic energy
$= \dfrac{1}{2} Mv^2+\dfrac{1}{2} \dfrac{2}{5} MR^2 \dfrac{v^2}{R^2}$
$= \dfrac{7}{10} Mv^2$
$= Mgh$
$v^2 = \dfrac{10gh}{7} \, $ OR $ \, v = \sqrt{\dfrac{10gh}{7}}$
Total kinetic energy = $\dfrac{1}{2} Mv^2+\dfrac{1}{2} Iω^2$
For rolling without slipping,
$v = ωR \, $ and $ \, I_{sphere} = \dfrac{2}{5} MR^2$
Thus, Total kinetic energy
$= \dfrac{1}{2} Mv^2+\dfrac{1}{2} \dfrac{2}{5} MR^2 \dfrac{v^2}{R^2}$
$= \dfrac{7}{10} Mv^2$
$= Mgh$
$v^2 = \dfrac{10gh}{7} \, $ OR $ \, v = \sqrt{\dfrac{10gh}{7}}$
Question 10 |
A block of mass $3m_o$ is tied with a pulley of mass $m_o$ and radius $r_o$, as shown below.
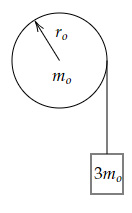
The system is released from rest. What will be the angular acceleration of the pulley when the block starts moving? (Assume the pulley is in the form of a disk with moment of inertia $\frac{1}{2} m_o r_o^2$.)
$\dfrac{g}{r_o}$ | |
$\dfrac{7}{8} \dfrac{g}{r_o}$ | |
$\dfrac{6}{7} \dfrac{g}{r_o}$ | |
$\dfrac{5}{6} \dfrac{g}{r_o}$ |
Question 10 Explanation:
From the free body diagram of the block
$3m_o g-T $ $ = 3m_o a … (1)$
From the free body diagram of the pulley
$Tr_o = Iα → T $ $ = \dfrac{1}{2} m_o r_o α … (2)$
Assuming the rope does not slip on the pulley,
$r_o α = a … (3)$
Using (2) and (3) in (1),
$3m_o g-\dfrac{1}{2} m_o a = 3m_o a$
On solving, $a = \dfrac{6}{7} g$
And, $α = \dfrac{6}{7} \dfrac{g}{r_o} $
$3m_o g-T $ $ = 3m_o a … (1)$
From the free body diagram of the pulley
$Tr_o = Iα → T $ $ = \dfrac{1}{2} m_o r_o α … (2)$
Assuming the rope does not slip on the pulley,
$r_o α = a … (3)$
Using (2) and (3) in (1),
$3m_o g-\dfrac{1}{2} m_o a = 3m_o a$
On solving, $a = \dfrac{6}{7} g$
And, $α = \dfrac{6}{7} \dfrac{g}{r_o} $
Question 11 |
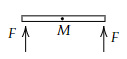
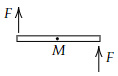
Which of the below options shows purely translational motion?
Choose two correct answers:
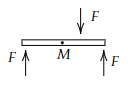 | |
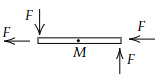 | |
 | |
 |
Question 11 Explanation:
Option A → Translational + Rotational
Option B → Translational + Rotational
Option C → Translational
Option D → Translational
Option B → Translational + Rotational
Option C → Translational
Option D → Translational
Question 12 |
The torque acting on an isolated system is zero. Which of the following is a correct conclusion from the information given?
The constituents of the system must be at rest | |
The center of mass of the system does not change with time | |
The system as a whole may perform circular motion | |
The system as a whole may perform non-linear oscillatory motion |
Question 12 Explanation:
Option A → Incorrect (The system could be moving in any fixed direction.)
Option B → Incorrect (The center of mass of the system may translate in any direction.)
Option C → Correct
Option D → Incorrect (Oscillatory motion may require torque to be non-zero at certain times, ex. simple pendulum.)
Option B → Incorrect (The center of mass of the system may translate in any direction.)
Option C → Correct
Option D → Incorrect (Oscillatory motion may require torque to be non-zero at certain times, ex. simple pendulum.)
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 12 questions to complete.
|
List |
More Practice Tests:
AP Physics 1 Main Menu >>
