This is Part 2 of our free AP Calculus AB unit test on derivatives. These questions cover differentiability, implicit differentiation, first derivative test, higher order derivatives, and the second derivative test. Understanding how to analyze function behavior using its derivatives will be necessary to do well on the AP Calculus AB exam.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
Identify $\frac{dy}{dx}$ for the following using implicit differentiation:
$2y^2 + 2x^2 = 4$
$\dfrac{dy}{dx} =$ $±\sqrt{2 − x^2}$ | |
$\dfrac{dy}{dx} =$ $x \cdot (2 − x^2)^{−\frac{1}{2}}$ | |
$\dfrac{dy}{dx} =$ $−\dfrac{x}{y}$ | |
$\text{DNE}$ |
Question 1 Explanation:
The correct answer is (C). This is where implicit techniques are necessary. Recall that when taking a derivative of any variable, $u$, with respect to a variable, $x$, the derivative is equal to the expression below:
$\dfrac{d(u)}{dx}$ $= (1)\dfrac{du}{dx}$
This is taken for granted while deriving equations isolated in terms of $x$ because the derivative of $x$ is $(1)\frac{dx}{dx}$ or $1$. Implicit differentiation is simply an extra consideration of chain rule.
Let’s apply this to the example. The derivative is taken in the normal way, just with the extra consideration for which variable is being derived. Be sure to take the derivative of both sides of the equation:
$2(2y)\left(\dfrac{dy}{dx}\right) +$ $2(2x)\left(\dfrac{dx}{dx}\right) = 0$
This simplifies to the form below. We must then isolate for $\frac{dy}{dx}$:
$\dfrac{dy}{dx}$ $= \dfrac{−4x}{4y}$ $= −\dfrac{x}{y}$
$\dfrac{d(u)}{dx}$ $= (1)\dfrac{du}{dx}$
This is taken for granted while deriving equations isolated in terms of $x$ because the derivative of $x$ is $(1)\frac{dx}{dx}$ or $1$. Implicit differentiation is simply an extra consideration of chain rule.
Let’s apply this to the example. The derivative is taken in the normal way, just with the extra consideration for which variable is being derived. Be sure to take the derivative of both sides of the equation:
$2(2y)\left(\dfrac{dy}{dx}\right) +$ $2(2x)\left(\dfrac{dx}{dx}\right) = 0$
This simplifies to the form below. We must then isolate for $\frac{dy}{dx}$:
$\dfrac{dy}{dx}$ $= \dfrac{−4x}{4y}$ $= −\dfrac{x}{y}$
Question 2 |
Identify $\frac{dy}{dt}$ for the following:
$2y = 3x^3 + \cos(x)$
$\dfrac{dy}{dt} =$ $\left(\dfrac{9}{2}x^2 − \dfrac{\sin(x)}{2}\right)\left(\dfrac{dx}{dt}\right)$ | |
$\dfrac{dy}{dt} =$ $(9x^2 − \sin(x))\left(\dfrac{dx}{dt}\right)$ | |
$\dfrac{dy}{dt} =$ $9x^2 − \sin(x)$ | |
$\dfrac{dy}{dt} =$ $\dfrac{9}{2}x^2 − \dfrac{\sin(x)}{2}$ |
Question 2 Explanation:
In this problem, we will not derive with respect to $x$ but rather with respect to $t$. Implicit differentiation allows for the derivative to be taken with respect to any variable. Be sure to recall all chain rules and trigonometric derivations.
$2\left(\dfrac{dy}{dt}\right) =$ $9x^2 \left(\dfrac{dx}{dt}\right) − \sin(x) \cdot \dfrac{dx}{dt}$
Then, we must isolate for $\frac{dy}{dt}$
$\dfrac{dy}{dt} =$ $\left(\dfrac{9}{2}x^2 − \dfrac{\sin(x)}{2}\right)\left(\dfrac{dx}{dt}\right)$
$2\left(\dfrac{dy}{dt}\right) =$ $9x^2 \left(\dfrac{dx}{dt}\right) − \sin(x) \cdot \dfrac{dx}{dt}$
Then, we must isolate for $\frac{dy}{dt}$
$\dfrac{dy}{dt} =$ $\left(\dfrac{9}{2}x^2 − \dfrac{\sin(x)}{2}\right)\left(\dfrac{dx}{dt}\right)$
Question 3 |
Identify the critical points of the following. (Only identify the $x$-values):
$f(x) = 3x^2 + 2x$
$x = 0$, $\; x = −\frac{2}{3}$ | |
$x = 0$ | |
$x = −\frac{1}{3}$ | |
$x = 0$, $\; x = −\frac{1}{3}$, $\;x = −\frac{2}{3}$ |
Question 3 Explanation:
The correct answer is (C). We must first take the derivative of the function and set is equal to zero to identify the function’s critical points.
$f'(x) = 6x + 2 = 0$
Then, solving for the roots of the derivative, we find that $x = −\frac{1}{3}$ is the only solution. This implies that this is the only critical point for the function.
$f'(x) = 6x + 2 = 0$
Then, solving for the roots of the derivative, we find that $x = −\frac{1}{3}$ is the only solution. This implies that this is the only critical point for the function.
Question 4 |
Identify the critical points of the following. (Only identify the $x$-values of the points):
$f(x) = \ln(x^2) + 3$
$\text{There are no}$ $\text{critical points.}$ | |
$x = 0$ | |
$x = 0$, $\; x = \sqrt{e^{–3}}$ | |
$x = ±\sqrt{e^{–3}}$ |
Question 4 Explanation:
The correct answer is (A). We must first take the derivative of the function and set it equal to zero to identify its critical points.
$f'(x) = \dfrac{1}{x^2} \cdot 2x$ $= \dfrac{2}{x} = 0$
Then, we can identify that there are no values of $x$ for which the derivative is equal to zero. Therefore, there are no critical points for the function.
$f'(x) = \dfrac{1}{x^2} \cdot 2x$ $= \dfrac{2}{x} = 0$
Then, we can identify that there are no values of $x$ for which the derivative is equal to zero. Therefore, there are no critical points for the function.
Question 5 |
Identify all extrema for the function below. Note that relative extrema are excluding any absolute extrema:
$f(x) = x^3 − 3x^2 + 2$
$\text{Absolute}$ $\text{maximum:}$ $(0, 0)$
$\text{Absolute}$ $\text{minimum:}$ $(0, 2)$ $\text{Relative}$ $\text{maxima:}$ $\text{None}$ $\text{Relative}$ $\text{minima:}$ $\text{None}$ | |
$\text{Absolute}$ $\text{maximum:}$ $(0, 2)$
$\text{Absolute}$ $\text{minimum:}$ $(2, -2)$ $\text{Relative}$ $\text{maxima:}$ $\text{None}$ $\text{Relative}$ $\text{minima:}$ $\text{None}$ | |
$\text{Absolute}$ $\text{maximum:}$ $\text{None}$
$\text{Absolute}$ $\text{minimum:}$ $\text{None}$ $\text{Relative}$ $\text{maxima:}$ $(0, 0)$ $\text{Relative}$ $\text{minima:}$ $(2, 0)$ | |
$\text{Absolute}$ $\text{maximum:}$ $\text{None}$
$\text{Absolute}$ $\text{minimum:}$ $\text{None}$ $\text{Relative}$ $\text{maxima:}$ $(0, 2)$ $\text{Relative}$ $\text{minima:}$ $(2, -2)$ |
Question 5 Explanation:
The correct answer is (D). We must first take the derivative of the function and set it equal to zero to identify the critical points of the function.
$f'(x)$ $= 3x^2 − 6x = 0$
Then, by factoring, we can identify the roots of the equation.
$f'(x)$ $= 3x(x − 2) = 0$
$x = 0$, $\; x = 2$
Now that we know the critical points, we must identify what type of extrema, if any, results from the critical values. We can do this by using the first derivative test. There are many ways to identify how $f'(x)$ changes across a critical value, including sign patterns, graphical analysis, or even just inspection. We will use the graph to identify how $f'(x)$ changes about the critical points.
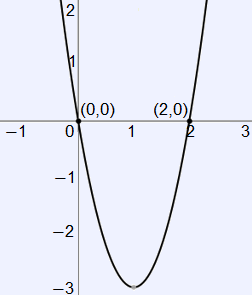
It is clear from the graph that $f'(x)$ changes from positive to negative about $x = 0$, and changes from negative to positive about $x = 2$. This implies that $x = 0$ is a relative maximum for $f(x)$ and $x = 2$ is a relative minimum for $f(x)$. We can then identify the function’s absolute maximum and minimum by identifying the values of the function at the ends of its domain, or its end behavior. We identify a functions end behavior using limits. We can evaluate these limits by direct substitution.
$\lim\limits_{x\to -\infty} f(x) = -\infty$
$\lim\limits_{x\to \infty} f(x) = \infty$
It is clear that $f(x)$ has no absolute maximum or minimum. Therefore, $f(x)$ only has the relative extrema resulting from the first derivative test. It is important not to forget to plug the critical values resulting in relative extrema back into the original function, as the question asks for the points of extrema, not just $x$-coordinates.
$f'(x)$ $= 3x^2 − 6x = 0$
Then, by factoring, we can identify the roots of the equation.
$f'(x)$ $= 3x(x − 2) = 0$
$x = 0$, $\; x = 2$
Now that we know the critical points, we must identify what type of extrema, if any, results from the critical values. We can do this by using the first derivative test. There are many ways to identify how $f'(x)$ changes across a critical value, including sign patterns, graphical analysis, or even just inspection. We will use the graph to identify how $f'(x)$ changes about the critical points.

It is clear from the graph that $f'(x)$ changes from positive to negative about $x = 0$, and changes from negative to positive about $x = 2$. This implies that $x = 0$ is a relative maximum for $f(x)$ and $x = 2$ is a relative minimum for $f(x)$. We can then identify the function’s absolute maximum and minimum by identifying the values of the function at the ends of its domain, or its end behavior. We identify a functions end behavior using limits. We can evaluate these limits by direct substitution.
$\lim\limits_{x\to -\infty} f(x) = -\infty$
$\lim\limits_{x\to \infty} f(x) = \infty$
It is clear that $f(x)$ has no absolute maximum or minimum. Therefore, $f(x)$ only has the relative extrema resulting from the first derivative test. It is important not to forget to plug the critical values resulting in relative extrema back into the original function, as the question asks for the points of extrema, not just $x$-coordinates.
Question 6 |
Identify all extrema for the function below. Note that relative extrema are excluding any absolute extrema.
$f(x) = \ln(x^2)$
$\text{Absolute}$ $\text{maximum:}$ $\text{None}$
$\text{Absolute}$ $\text{minimum:}$ $\text{None}$ $\text{Relative}$ $\text{maxima:}$ $(−\sqrt{e}, 0)$ $\text{Relative}$ $\text{minima:}$ $(\sqrt{e}, 0)$ | |
$\text{Absolute}$ $\text{maximum:}$ $(−\sqrt{e}, 0)$
$\text{Absolute}$ $\text{minimum:}$ $(\sqrt{e}, 0)$ $\text{Relative}$ $\text{maxima:}$ $\text{None}$ $\text{Relative}$ $\text{minima:}$ $\text{None}$ | |
$\text{Absolute}$ $\text{maximum:}$ $\text{None}$
$\text{Absolute}$ $\text{minimum:}$ $\text{None}$ $\text{Relative}$ $\text{maxima:}$ $\text{None}$ $\text{Relative}$ $\text{minima:}$ $\text{None}$ | |
$\text{Absolute}$ $\text{maximum:}$ $\text{None}$
$\text{Absolute}$ $\text{minimum:}$ $(0,0)$ $\text{Relative}$ $\text{maxima:}$ $(−\sqrt{e}, 0)$ $\text{Relative}$ $\text{minima:}$ $(\sqrt{e}, 0)$ |
Question 6 Explanation:
The correct answer is (C). We must first identify the derivative of the function and set is equal to zero to identify the critical points for the function.
$f'(x) = \dfrac{1}{x^2} \cdot 2x$ $= \dfrac{2}{x} = 0$
Now, it is clear at this point that there are no values of $x$ that are critical points for the function. Therefore, no relative extrema exist. However, we must also identify if there exist absolute extrema. We can identify absolute extrema through identifying the functions end behavior. These limits below can be evaluated by direct substitution.
$\lim\limits_{x\to -\infty} f(x) = \infty$
$\lim\limits_{x\to \infty} f(x) = \infty$
However, it is also important to check for the values at discontinuities for the function. It is clear that $f(x)$ is not defined at $x = 0$, meaning that there exists a vertical asymptote at $x = 0$.
$\lim\limits_{x\to 0} f(x) = –\infty$
Therefore, there do not exist absolute extrema for the function either. This would also be clear if the graph of the function was analyzed.
$f'(x) = \dfrac{1}{x^2} \cdot 2x$ $= \dfrac{2}{x} = 0$
Now, it is clear at this point that there are no values of $x$ that are critical points for the function. Therefore, no relative extrema exist. However, we must also identify if there exist absolute extrema. We can identify absolute extrema through identifying the functions end behavior. These limits below can be evaluated by direct substitution.
$\lim\limits_{x\to -\infty} f(x) = \infty$
$\lim\limits_{x\to \infty} f(x) = \infty$
However, it is also important to check for the values at discontinuities for the function. It is clear that $f(x)$ is not defined at $x = 0$, meaning that there exists a vertical asymptote at $x = 0$.
$\lim\limits_{x\to 0} f(x) = –\infty$
Therefore, there do not exist absolute extrema for the function either. This would also be clear if the graph of the function was analyzed.
Question 7 |
Let the graph below represent the first derivative of the function $f(x)$. Identify the $x$-values for all extrema of $f(x)$. Note that relative extrema is excluding any absolute extrema.
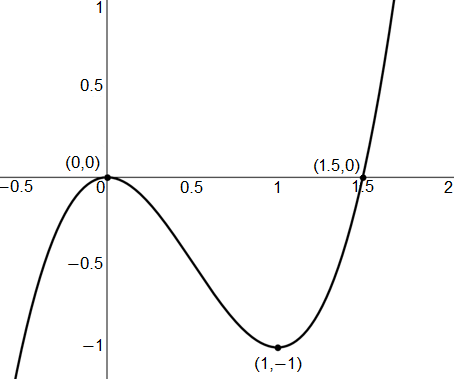

$\text{Absolute}$ $\text{maximum:}$ $\text{None}$
$\text{Absolute}$ $\text{minimum:}$ $\text{None}$ $\text{Relative}$ $\text{maxima:}$ $\text{None}$ $\text{Relative}$ $\text{minima:}$ $x = 1.5$ | |
$\text{Absolute}$ $\text{maximum:}$ $\text{None}$
$\text{Absolute}$ $\text{minimum:}$ $x = 1.5$ $\text{Relative}$ $\text{maxima:}$ $\text{None}$ $\text{Relative}$ $\text{minima:}$ $\text{None}$ | |
$\text{Absolute}$ $\text{maximum:}$ $\text{None}$
$\text{Absolute}$ $\text{minimum:}$ $\text{None}$ $\text{Relative}$ $\text{maxima:}$ $\text{None}$ $\text{Relative}$ $\text{minima:}$ $\text{None}$ | |
$\text{Absolute}$ $\text{maximum:}$ $\text{None}$
$\text{Absolute}$ $\text{minimum:}$ $\text{None}$ $\text{Relative}$ $\text{maxima:}$ $x = 0$ $\text{Relative}$ $\text{minima:}$ $x = 1.5$ |
Question 7 Explanation:
The correct answer is (B). We can use the given graph of the derivative of the function to identify critical points. It is clear that the derivative is equal to zero at $x = 0$ and $x = 1.5$. We can then apply the first derivative test to identify local extrema for $f(x)$. it is clear that $f'(x)$ changes from negative to positive about $x = 1.5$, but $f'(x)$ does not change signs about $x = 0$. Therefore, only $x = 1.5$ is a relative minimum for $f(x)$.
Now, identifying the extrema for $f(x)$ is a bit more tricky. It is very important to identify that the given derivative function is “cubic” in shape, so the derivative is at least a polynomial of an odd degree. This then implies that its function, $f(x)$, must be of even degree. It is important to recall the general shape of higher order polynomials. We then know that $f(x)$ has a “U” shape as it is a polynomial of even degree, which means that there does not exist an absolute maximum, but there does exist an absolute minimum, which is the vertex of the “U.” This vertex is also a local minimum for the graph, and we have already identified that there exists a local minimum for the function at $x = 1.5$. Therefore, it is clear that the absolute minimum for the function is also at $x = 1.5$.
Now, identifying the extrema for $f(x)$ is a bit more tricky. It is very important to identify that the given derivative function is “cubic” in shape, so the derivative is at least a polynomial of an odd degree. This then implies that its function, $f(x)$, must be of even degree. It is important to recall the general shape of higher order polynomials. We then know that $f(x)$ has a “U” shape as it is a polynomial of even degree, which means that there does not exist an absolute maximum, but there does exist an absolute minimum, which is the vertex of the “U.” This vertex is also a local minimum for the graph, and we have already identified that there exists a local minimum for the function at $x = 1.5$. Therefore, it is clear that the absolute minimum for the function is also at $x = 1.5$.
Question 8 |
Identify the 2nd derivative of the function below:
$f(x) = \sin^3(3x)$
$f''(x) =$ $54\sin(3x)$ | |
$f''(x) =$ $9\sin^2(3x) \cos(3x)$ | |
$f''(x) =$ $27\sin^3(3x) + 54\cos^2(3x) \sin(3x)$ | |
$f''(x) =$ $−27\sin^3(3x) + 54\cos^2(3x) \sin(3x)$ |
Question 8 Explanation:
The correct answer is (D). Be careful with chain rule and power rule.
$f'(x) = $ $3(\sin^2(3x)) \cdot (\cos(3x) \cdot 3)$ $= 9\sin^2(3x) \cdot \cos(3x)$
Don’t forget to use product rule for the second derivative.
$f''(x) = $ $9\sin^2(3x)(−3\sin(3x))$
$+ \cos(3x) (18\sin(3x) \cdot 3\cos (3x))$
$= −27\sin^3(3x) + 54\cos^2(3x) \sin(3x)$
$f'(x) = $ $3(\sin^2(3x)) \cdot (\cos(3x) \cdot 3)$ $= 9\sin^2(3x) \cdot \cos(3x)$
Don’t forget to use product rule for the second derivative.
$f''(x) = $ $9\sin^2(3x)(−3\sin(3x))$
$+ \cos(3x) (18\sin(3x) \cdot 3\cos (3x))$
$= −27\sin^3(3x) + 54\cos^2(3x) \sin(3x)$
Question 9 |
Identify the 5thderivative of the function below:
$f(x) = \ln(2x)$
$f^{(5)} = \dfrac{24}{x^5}$ | |
$f^{(5)} = \dfrac{−24}{x^5}$ | |
$f^{(5)} = \dfrac{6}{x^4}$ | |
$f^{(5)} = \dfrac{–6}{x^4}$ |
Question 9 Explanation:
The correct answer is (A). Be careful with power rule and recall that the derivative of the natural log function is:
$\frac{d}{du}\ln(u)$ $= \frac{1}{u} \cdot du$
$f'(x) = \dfrac{1}{2x} \cdot 2$ $= \dfrac{1}{x}$
The following derivatives may be more clear if the first derivative is written $f'(x) = x^{−1}$.
$f''(x) = −\frac{1}{x^2}$
This idea of rewriting these rational functions with negative exponents can be used to help identify the remaining higher order derivatives.
$f'''(x) = \dfrac{2}{x^3}$
$f^4(x) = −\dfrac{6}{x^4}$
$f^{(5)} = \dfrac{24}{x^5}$
$\frac{d}{du}\ln(u)$ $= \frac{1}{u} \cdot du$
$f'(x) = \dfrac{1}{2x} \cdot 2$ $= \dfrac{1}{x}$
The following derivatives may be more clear if the first derivative is written $f'(x) = x^{−1}$.
$f''(x) = −\frac{1}{x^2}$
This idea of rewriting these rational functions with negative exponents can be used to help identify the remaining higher order derivatives.
$f'''(x) = \dfrac{2}{x^3}$
$f^4(x) = −\dfrac{6}{x^4}$
$f^{(5)} = \dfrac{24}{x^5}$
Question 10 |
Identify any points of inflection for the function below:
$f(x) = 2x^3 + 3x^2$
$\text{No}$ $\text{points}$ $\text{of}$ $\text{inflection}$ | |
$(0, 0)$ $\text{and}$ $(–1, 1)$ | |
$\left(–\dfrac{1}{2}, \dfrac{1}{2}\right)$ | |
$\left(–\dfrac{1}{2}, 0\right)$ |
Question 10 Explanation:
The correct answer is (C). We must identify the second derivative for the function and set it equal to zero to identify points of inflection.
$f'(x) = 6x^2 + 6x$
$f''(x) = 12x + 6$ $=0$
Then, it is clear that the roots of the second derivative are $x = −\frac{1}{2}$.
Therefore, $f(x)$ has a point of inflection about $x = −\frac{1}{2}$. Don’t forget to plug in this $x$-value back into the original function to identify the point of inflection, as the question does not just ask for the $x$-coordinate.
$f'(x) = 6x^2 + 6x$
$f''(x) = 12x + 6$ $=0$
Then, it is clear that the roots of the second derivative are $x = −\frac{1}{2}$.
Therefore, $f(x)$ has a point of inflection about $x = −\frac{1}{2}$. Don’t forget to plug in this $x$-value back into the original function to identify the point of inflection, as the question does not just ask for the $x$-coordinate.
Question 11 |
Identify the points of inflection for the function below:
$f(x) = e^{3x^2 + 2}$
$(\frac{\sqrt{6}}{6}, e^{\frac{5}{2}})$ | |
$(−\frac{\sqrt{6}}{6}, e^{\frac{5}{2}})$ | |
$(\frac{\sqrt{6}}{6}, e^{\frac{5}{2}})$, $(−\frac{\sqrt{6}}{6}, e^{\frac{5}{2}})$ | |
$\text{No}$ $\text{points}$ $\text{of}$ $\text{inflection.}$ |
Question 11 Explanation:
The correct answer is (D). We must identify the second derivative for the function and set it equal to zero to identify points of inflection.
$f'(x) = (6x) \cdot e^{3x^2 + 2}$
$f'(x) =$ $6x(6x) \cdot e^{3x^2 + 2} + 6e^{3x^2 + 2}$
$= e^{3x^2 + 2}(36x^2 + 6) = 0$
It is clear at this point that there is no point of inflection for $f(x)$, as the only possible root does not exist, as there is no square root for the value below.
$x^2 = −\frac{1}{6}$
Similarly, $e^{3x^2 + 2} ≠ 0$ for all real values of $x$.
Therefore, there are no points of inflection.
$f'(x) = (6x) \cdot e^{3x^2 + 2}$
$f'(x) =$ $6x(6x) \cdot e^{3x^2 + 2} + 6e^{3x^2 + 2}$
$= e^{3x^2 + 2}(36x^2 + 6) = 0$
It is clear at this point that there is no point of inflection for $f(x)$, as the only possible root does not exist, as there is no square root for the value below.
$x^2 = −\frac{1}{6}$
Similarly, $e^{3x^2 + 2} ≠ 0$ for all real values of $x$.
Therefore, there are no points of inflection.
Question 12 |
Identify where the function below is concave up:
$f(x) = 6x^3 + 3x^2 + 2x$
$\text{The}$ $\text{function}$ $\text{is}$ $\text{not}$ $\text{concave}$ $\text{up}$ $\text{anywhere}$ $\text{on}$ $\text{its}$ $\text{domain.}$ | |
$(−\frac{1}{6}, \infty)$ | |
$[−\frac{1}{6}, \infty)$ | |
$(−\infty, \infty)$ |
Question 12 Explanation:
The correct answer is (B). We must first identify the second derivative and any points of inflection for the function before identifying overall concavity.
$f'(x) = 18x^2 + 6x + 2$
$f''(x) = 36x + 6$
Then, after setting the second derivative equal to zero, it is clear that there is a point of inflection at $x = −\frac{1}{6}$. We can identify the concavity of the function based on the graph of the second derivative.
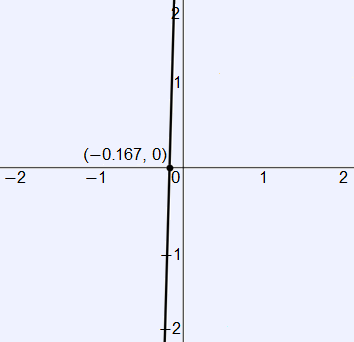
It is clear that the second derivative is negative at all values of $x$ before $x = −\frac{1}{6}$ and positive at all values after. Therefore, $f(x)$ is concave up on the domain $x > −\frac{1}{6}$, or $(−\frac{1}{6}, \infty)$
$f'(x) = 18x^2 + 6x + 2$
$f''(x) = 36x + 6$
Then, after setting the second derivative equal to zero, it is clear that there is a point of inflection at $x = −\frac{1}{6}$. We can identify the concavity of the function based on the graph of the second derivative.

It is clear that the second derivative is negative at all values of $x$ before $x = −\frac{1}{6}$ and positive at all values after. Therefore, $f(x)$ is concave up on the domain $x > −\frac{1}{6}$, or $(−\frac{1}{6}, \infty)$
Question 13 |
Identify where the following function is concave down on the given domain:
$f(x) = \sin(3x), −\frac{π}{3} ≤ x ≤ \frac{π}{3}$
$(0, \frac{π}{3})$ | |
$[0, \frac{π}{3}]$ | |
$ (−\frac{π}{3}, 0)$, $(0, \frac{π}{3})$ | |
$\text{The}$ $\text{function}$ $\text{is}$ $\text{not}$ $\text{concave}$ $\text{down}$ $\text{anywhere}$ $\text{on}$ $\text{the}$ $\text{domain.}$ |
Question 13 Explanation:
The correct answer is (A). We must first identify the second derivative and any points of inflection to identify the function’s concavity.
$f'(x) = 3 \cos(3x)$
$f''(x) = −9\sin(3x)$
Now, it is clear that the second derivative has roots at $x = −\frac{π}{3}$, $x = 0$, and $x = \frac{π}{3}$ on the given domain, which implies that $f(x)$ has a point of inflection at $x = 0$. Notice that the other two roots are not considered points of inflection, as $f(x)$ cannot change inflection about a point if that is an endpoint. Then, we can observe the concavity of the function from the graph of the second derivative.
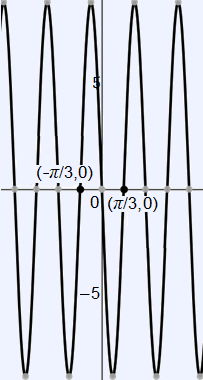
It is clear from the graph that the second derivative is positive from $ (−\frac{π}{3}, 0)$ and negative from $(0, \frac{π}{3})$. Therefore, $f(x)$ is concave down from $(0, \frac{π}{3})$
$f'(x) = 3 \cos(3x)$
$f''(x) = −9\sin(3x)$
Now, it is clear that the second derivative has roots at $x = −\frac{π}{3}$, $x = 0$, and $x = \frac{π}{3}$ on the given domain, which implies that $f(x)$ has a point of inflection at $x = 0$. Notice that the other two roots are not considered points of inflection, as $f(x)$ cannot change inflection about a point if that is an endpoint. Then, we can observe the concavity of the function from the graph of the second derivative.

It is clear from the graph that the second derivative is positive from $ (−\frac{π}{3}, 0)$ and negative from $(0, \frac{π}{3})$. Therefore, $f(x)$ is concave down from $(0, \frac{π}{3})$
Question 14 |
Identify where the function $f(x)$ is concave up and concave down given the graph of the second derivative below.


$\text{Concave Down:}$ $\text{Nowhere}$ $\text{on}$ $\text{the}$ $\text{domain.}$
$\text{Concave}$ $\text{Up:}$ $(−\infty, \infty)$ | |
$\text{Concave Down:}$ $(−1, \infty)$
$\text{Concave}$ $\text{Up:}$ $(–\infty, –1)$ | |
$\text{Concave Down:}$ $(−\infty, 0)$
$\text{Concave}$ $\text{Up:}$ $(0, \infty)$ | |
$\text{Concave Down:}$ $(−\infty, −1)$
$\text{Concave}$ $\text{Up:}$ $(−1, \infty)$ |
Question 14 Explanation:
The correct answer is (D). It is clear that there exists a point of inflection for the function at $x = −1$, as $f''(−1) = 0$ by the given graph.
Similarly, it can be identified that $f''(x)$ is negative for $(−\infty, −1)$ and is positive for $(−1, \infty)$. Therefore, $f(x)$ must be concave down for $(−\infty, −1)$ and concave up for $(−1, \infty)$.
Similarly, it can be identified that $f''(x)$ is negative for $(−\infty, −1)$ and is positive for $(−1, \infty)$. Therefore, $f(x)$ must be concave down for $(−\infty, −1)$ and concave up for $(−1, \infty)$.
Question 15 |
Identify the concavity and the points of inflection for the function $f(x)$ given graph of the first derivative of the function, $f'(x)$, below.
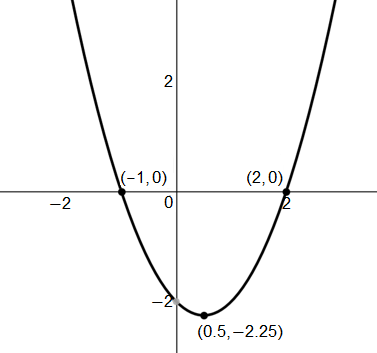

$\text{Point(s)}$ $\text{of}$ $\text{inflection}$ $\text{at}$ $\text{no}$ $\text{values}$ $\text{of}$ $x.$
$\text{Concave Down:}$ $\text{Nowhere}$ $\text{on}$ $\text{the}$ $\text{domain.}$ $\text{Concave}$ $\text{Up:}$ $(−\infty, \infty)$ | |
$\text{Point(s)}$ $\text{of}$ $\text{inflection}$ $\text{at}$ $x = −1$, $x = 2$
$\text{Concave Down:}$ $(−1, 2)$ $\text{Concave}$ $\text{Up:}$ $(−\infty, −1)$U$(2, \infty)$ | |
$\text{Point(s)}$ $\text{of}$ $\text{inflection}$ $\text{at}$ $x = 0.5$
$\text{Concave Down:}$ $(−\infty, 0.5)$ $\text{Concave}$ $\text{Up:}$ $(0.5, \infty)$ | |
$\text{Point(s)}$ $\text{of}$ $\text{inflection}$ $\text{at}$ $x = 0.5$
$\text{Concave Down:}$ $(0.5, −\infty)$ $\text{Concave}$ $\text{Up:}$ $(\infty, 0.5)$ |
Question 15 Explanation:
The correct answer is (C). It is important to recognize that the concavity and points of inflection cannot be observed directly from the given graph, as it is not the graph of the second derivative. We must visualize the graph of the second derivative using the given graph. Recall that the derivative is simply a function whose output measures the slope of the tangent line to the curve at the given point. Thus, we can visualize the second derivative graph by visualizing tangent lines to the given graph.
We know that there exists a point of inflection for the function at $x = 0.5$, as the tangent line to the first derivative graph at $x = 0.5$ would have a slope of $0$, which implies that $f''(0.5) = 0$.
Then, we can similarly identify that all the tangent lines to the given graph prior to $x = 0.5$ would be negative or “downward-sloping,” which implies that the derivative of the given graph would be negative at these values. Similarly, all the tangent lines to the given graph after $x = 0.5$ would be positive or “upward-sloping,” which implies that the derivative of the given graph would be positive at these values.
Thus, $f''(x) > 0$ for all $x > 0.5$ and $f''(x) < 0$ for all $x < 0.5$. Therefore, $f(x)$ is concave down on $(−\infty, 0.5)$, is concave up on $(0.5, \infty)$, and has a point of inflection at $x = 0.5$.
We know that there exists a point of inflection for the function at $x = 0.5$, as the tangent line to the first derivative graph at $x = 0.5$ would have a slope of $0$, which implies that $f''(0.5) = 0$.
Then, we can similarly identify that all the tangent lines to the given graph prior to $x = 0.5$ would be negative or “downward-sloping,” which implies that the derivative of the given graph would be negative at these values. Similarly, all the tangent lines to the given graph after $x = 0.5$ would be positive or “upward-sloping,” which implies that the derivative of the given graph would be positive at these values.
Thus, $f''(x) > 0$ for all $x > 0.5$ and $f''(x) < 0$ for all $x < 0.5$. Therefore, $f(x)$ is concave down on $(−\infty, 0.5)$, is concave up on $(0.5, \infty)$, and has a point of inflection at $x = 0.5$.
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 15 questions to complete.
|
List |
Next Practice Test:
Derivatives Part 3 >>
AP Calculus Menu >>
