The PSAT includes two sections of math: Calculator & No Calculator. This PSAT Math practice test is designed to be taken without a calculator. The PSAT Math test covers the types of math problems that you are likely to encounter in college math, science, and social science courses. Topics include algebra, problem solving, data analysis, and advanced math.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
George takes 3 hours to mow a lawn. Jacob takes 6 hours to mow the same lawn. How long will it take if both of them mow 3 lawns together?
$3$ | |
$6$ | |
$9$ | |
$12$ |
Question 1 Explanation:
The correct answer is (B).
George takes 3 hrs/lawn, so his rate of work is $\frac{1}{3}$ lawn/hr.
Jacob takes 6 hrs/lawn, so his rate of work is $\frac{1}{6}$ lawn/hr.
If they work together, they will mow $\frac{1}{3} + \frac{1}{6} = \frac{1}{2}$ lawn/hr.
We can now set up equivalent proportions:
$\dfrac{\frac{1}{2} \text{ lawn}}{1 \text{ hour}}$ $= \dfrac{3 \text{ lawns}}{x \text{ hours}}$
Cross multiplying, we get:
$(1)(3) = \left(\dfrac{1}{2}\right)(x)$
$3 = \dfrac{1}{2}x$
$x = 6 \text{ hours}$
George takes 3 hrs/lawn, so his rate of work is $\frac{1}{3}$ lawn/hr.
Jacob takes 6 hrs/lawn, so his rate of work is $\frac{1}{6}$ lawn/hr.
If they work together, they will mow $\frac{1}{3} + \frac{1}{6} = \frac{1}{2}$ lawn/hr.
We can now set up equivalent proportions:
$\dfrac{\frac{1}{2} \text{ lawn}}{1 \text{ hour}}$ $= \dfrac{3 \text{ lawns}}{x \text{ hours}}$
Cross multiplying, we get:
$(1)(3) = \left(\dfrac{1}{2}\right)(x)$
$3 = \dfrac{1}{2}x$
$x = 6 \text{ hours}$
Question 2 |
A new electric hybrid car has a gas mileage of 45 miles per gallon. The car has a gas tank that holds 16 gallons of gas. The car with a half-full tank is driven at 90 miles an hour.
Which of the following functions $f$ models the amount of gas remaining in the tank after $t$ hours?$f(t) = 8 − 2t$ | |
$f(t) = 8 + 2t$ | |
$f(t) = 16 − t$ | |
$f(t) = 16 − 2t$ |
Question 2 Explanation:
The correct answer is (A). The car starts off with 8 gallons of gas. We need to find "gallons per hour".
$\dfrac{45 \text{ miles}}{1 \text{ gallon}}$ $\text{ or }$ $\dfrac{1 \text{ gallon}}{45 \text{ miles}}$
$\require{cancel} \dfrac{1 \text{ gallon}}{45 \cancel{\text{ miles}}} \cdot \dfrac{90 \cancel{\text{ miles}}}{1 \text{ hour}}$
$= \dfrac{(1)(90) \text{ gallons}}{(45)(1) \text{ hours}}$
$= \dfrac{90 \text{ gallons}}{45 \text{ hours}}$
$= \dfrac{2 \text{ gallons}}{1 \text{ hour}}$
Each hour ($t$), it loses 2 gallons of gas. This is represented by $f(t) = 8 − 2t$.
$\dfrac{45 \text{ miles}}{1 \text{ gallon}}$ $\text{ or }$ $\dfrac{1 \text{ gallon}}{45 \text{ miles}}$
$\require{cancel} \dfrac{1 \text{ gallon}}{45 \cancel{\text{ miles}}} \cdot \dfrac{90 \cancel{\text{ miles}}}{1 \text{ hour}}$
$= \dfrac{(1)(90) \text{ gallons}}{(45)(1) \text{ hours}}$
$= \dfrac{90 \text{ gallons}}{45 \text{ hours}}$
$= \dfrac{2 \text{ gallons}}{1 \text{ hour}}$
Each hour ($t$), it loses 2 gallons of gas. This is represented by $f(t) = 8 − 2t$.
Question 3 |
There are two pizza ovens in a restaurant. Oven #1 burns three times as many pizzas as Oven #2. If the restaurant had a total of 12 burnt pizzas on Saturday, how many pizzas did Oven #2 burn?
$2$ | |
$3$ | |
$4$ | |
$5$ |
Question 3 Explanation:
The correct answer is (B). Begin by expressing the relationship between the ovens with an equation. Use a variable to represent the number of burnt pizzas. For every $x$ pizzas burnt by Oven #2, Oven #1 burns 3$x$ pizzas. It is given that 12 total pizzas are burnt, and the total number of burnt pizzas is a combination of pizzas burnt by Oven #1 and Oven #2:
$x + 3x = 12$
$4x = 12$
$x = 3$
$x + 3x = 12$
$4x = 12$
$x = 3$
Question 4 |
If the two roots of $6x^2 + 6x = 12$ are $r_1$ and $r_2$, what is the product $r_1 \cdot r_2$?
$−2$ | |
$−1$ | |
$1$ | |
$2$ |
Question 4 Explanation:
The correct answer is (A). Dividing the equation by 6 gives:
$x^2 + x − 2 = 0$
Factoring gives:
$(x - 1) (x + 2) = 0$
The roots are 1 and −2. The product of the roots is:
$1 \cdot −2 = −2$
$x^2 + x − 2 = 0$
Factoring gives:
$(x - 1) (x + 2) = 0$
The roots are 1 and −2. The product of the roots is:
$1 \cdot −2 = −2$
Question 5 |
The function $f(x) = ax + 2 + c\,$ passes through the points (0, 4) and (−1, 2). What is the value of $a + c\,$?
$2$ | |
$4$ | |
$6$ | |
$8$ |
Question 5 Explanation:
The correct answer is (B).
$f(x) = ax + 2 + c$
Since the slope-intercept form of a line is $y = mx + b$, $m = a$ (our slope is "$a$") and $b = 2 + c\,$ (our $y$-intercept is "$2 + c$").
Since the point (0, 4) lies on the line, we know the $y$-intercept is 4.
$2 + c = 4$
$c = 2$
$\text{Slope } m = \dfrac{y_2 − y_1}{x_2 − x_1}$
$= \dfrac{2 − 4}{−1 − 0}$ $= \dfrac{−2}{−1} = 2$
$a = 2$
We are asked to find $a + c$:
$a + c = 2 + 2 = 4$
$f(x) = ax + 2 + c$
Since the slope-intercept form of a line is $y = mx + b$, $m = a$ (our slope is "$a$") and $b = 2 + c\,$ (our $y$-intercept is "$2 + c$").
Since the point (0, 4) lies on the line, we know the $y$-intercept is 4.
$2 + c = 4$
$c = 2$
$\text{Slope } m = \dfrac{y_2 − y_1}{x_2 − x_1}$
$= \dfrac{2 − 4}{−1 − 0}$ $= \dfrac{−2}{−1} = 2$
$a = 2$
We are asked to find $a + c$:
$a + c = 2 + 2 = 4$
Question 6 |
$3x + 2y = 6$
$7x + 4y = 9$
Based on the system of equations above, what is the value of the product $xy$?
$−\dfrac{45}{2}$ | |
$−\dfrac{9}{2}$ | |
$−3$ | |
$\dfrac{15}{2}$ |
Question 6 Explanation:
The correct answer is (A). Solve the system of linear equations:
$3x + 2y = 6$
$7x + 4y = 9$
Multiply the first equation by 2 throughout:
$6x + 4y = 12$
$7x + 4y = 9$
Subtract the first equation from the second:
$~~~~7x + 4y = 9$
$−(6x + 4y = 12)$
––––––––––––––––––
$~~~x = −3$
Substitute $x = −3$ into either equation:
$7x + 4y = 9$
$7(−3) + 4y = 9$
$−21 + 4y = 9$
$4y = 30$
$y = \dfrac{30}{4}$
$y = \dfrac{15}{2}$
The product is: $−3 \cdot \dfrac{15}{2} = −\dfrac{45}{2}$
$3x + 2y = 6$
$7x + 4y = 9$
Multiply the first equation by 2 throughout:
$6x + 4y = 12$
$7x + 4y = 9$
Subtract the first equation from the second:
$~~~~7x + 4y = 9$
$−(6x + 4y = 12)$
––––––––––––––––––
$~~~x = −3$
Substitute $x = −3$ into either equation:
$7x + 4y = 9$
$7(−3) + 4y = 9$
$−21 + 4y = 9$
$4y = 30$
$y = \dfrac{30}{4}$
$y = \dfrac{15}{2}$
The product is: $−3 \cdot \dfrac{15}{2} = −\dfrac{45}{2}$
Question 7 |
$f(x + 1) = 3(x + 2)$ for all values of $x$. What is the value of $f(−7)$?
$−12$ | |
$−18$ | |
$−15$ | |
$−21$ |
Question 7 Explanation:
The correct answer is (B).
We are being asked to find $f(−7)$. Since we know that $f(x + 1) = 3(x + 2)$, if we can get the $f(x + 1)$ to equal $f(−7)$ then we can solve this question.
For $f(x + 1)$ to be equal to $f(−7)$, $x + 1$ must equal $−7$.
$x + 1 = −7$
Subtracting $1$ from both sides gives:
$x = −8$
When $x = −8$, $f(x + 1) = f(−7)$.
We can now plug $x = −8$ back into the original equation:
$f(x + 1) = 3(x + 2)$
$f(−8 + 1) = 3(−8 + 2)$
$f(−7) = 3(−6)$
$f(−7) = −18$
We are being asked to find $f(−7)$. Since we know that $f(x + 1) = 3(x + 2)$, if we can get the $f(x + 1)$ to equal $f(−7)$ then we can solve this question.
For $f(x + 1)$ to be equal to $f(−7)$, $x + 1$ must equal $−7$.
$x + 1 = −7$
Subtracting $1$ from both sides gives:
$x = −8$
When $x = −8$, $f(x + 1) = f(−7)$.
We can now plug $x = −8$ back into the original equation:
$f(x + 1) = 3(x + 2)$
$f(−8 + 1) = 3(−8 + 2)$
$f(−7) = 3(−6)$
$f(−7) = −18$
Question 8 |
$\dfrac{1}{2}x − \dfrac{1}{4}y = 5$
$14x − by = 140$
In the system of linear equations above, $b$ is a constant. If the system has infinite solutions, what is the value of $b$?
$5$ | |
$7$ | |
$28$ | |
$56$ |
Question 8 Explanation:
The correct answer is (B). Multiplying the first equation by 28 gives:
$(28)(\frac{1}{2}x) + (28)(−\frac{1}{4}y)$ $= (28)(5)$
$14x − 7y = 140$
$14x − by = 140$
Since the system has infinite solutions, the equations/lines are the same. So, $b = 7$.
$(28)(\frac{1}{2}x) + (28)(−\frac{1}{4}y)$ $= (28)(5)$
$14x − 7y = 140$
$14x − by = 140$
Since the system has infinite solutions, the equations/lines are the same. So, $b = 7$.
Question 9 |
If $b$ is a fraction such that $\frac{1}{2} < b < \frac{2}{3}$, which of the following is a true statement?
$b > b^2 < b^{−3}$ | |
$b < b^2 < b^{−3}$ | |
$b > b^2 > b^{−3}$ | |
$b > b^{−3} < b^2$ |
Question 9 Explanation:
The correct answer is (A). Use the fact that multiplying a fraction (less than 1) by itself will make the result smaller each time. Thus $b$ will be greater than $b^n$ when $n>1$.
Similarly, when a fraction (less than 1) is taken to a negative power, the result will be greater than the original fraction.
Using these facts, you can conclude that the correct choice is (A).
An alternative approach is to find a value of $b$ that can be used to test each of the four answer choices.
Something very helpful to realize in this question is that even though $b$ technically must be greater than $\frac{1}{2}$ and less than $\frac{2}{3}$, whether we let $b = \frac{7}{12}$ (a fraction half-way between $\frac{1}{2}$ and $\frac{2}{3}$) or we let $b = \frac{1}{2}$, they will behave the same for the purpose of testing each of the four answer choices.
To keep the math simpler let's use $b = \dfrac{1}{2}$.
$b^2 = \left(\dfrac{1}{2}\right)^2 = \left(\dfrac{1}{2}\right)\left(\dfrac{1}{2}\right)$ $ =\dfrac{1}{4}$
$b^{−3} = \left(\dfrac{1}{2}\right)^{−3} = \dfrac{1}{\left(\frac{1}{2}\right)^3}$
$= \dfrac{1}{\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)} = \dfrac{1}{\left(\frac{1}{8}\right)}$
$= (1)\left(\dfrac{8}{1}\right) = 8$
Plugging these results into the four answer choices gives:
(A) $\dfrac{1}{2} > \dfrac{1}{4} < 8$ True
(B) $\dfrac{1}{2} < \dfrac{1}{4} < 8$ False
(C) $\dfrac{1}{2} > \dfrac{1}{4} > 8$ False
(D) $\dfrac{1}{2} > 8 < \dfrac{1}{4}$ False
Only (A) is a valid inequality.
Similarly, when a fraction (less than 1) is taken to a negative power, the result will be greater than the original fraction.
Using these facts, you can conclude that the correct choice is (A).
An alternative approach is to find a value of $b$ that can be used to test each of the four answer choices.
Something very helpful to realize in this question is that even though $b$ technically must be greater than $\frac{1}{2}$ and less than $\frac{2}{3}$, whether we let $b = \frac{7}{12}$ (a fraction half-way between $\frac{1}{2}$ and $\frac{2}{3}$) or we let $b = \frac{1}{2}$, they will behave the same for the purpose of testing each of the four answer choices.
To keep the math simpler let's use $b = \dfrac{1}{2}$.
$b^2 = \left(\dfrac{1}{2}\right)^2 = \left(\dfrac{1}{2}\right)\left(\dfrac{1}{2}\right)$ $ =\dfrac{1}{4}$
$b^{−3} = \left(\dfrac{1}{2}\right)^{−3} = \dfrac{1}{\left(\frac{1}{2}\right)^3}$
$= \dfrac{1}{\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)} = \dfrac{1}{\left(\frac{1}{8}\right)}$
$= (1)\left(\dfrac{8}{1}\right) = 8$
Plugging these results into the four answer choices gives:
(A) $\dfrac{1}{2} > \dfrac{1}{4} < 8$ True
(B) $\dfrac{1}{2} < \dfrac{1}{4} < 8$ False
(C) $\dfrac{1}{2} > \dfrac{1}{4} > 8$ False
(D) $\dfrac{1}{2} > 8 < \dfrac{1}{4}$ False
Only (A) is a valid inequality.
Question 10 |
At Sing & Dance, customers can rent singing and dancing rooms. The cost for renting the singing room is \$10 per minute and the cost for renting the dancing room is \$20 per minute. Sienna rented the rooms for a combined total of 48 minutes and a total cost of \$600. For how many minutes did she rent the singing room?
$12$ | |
$16$ | |
$36$ | |
$32$ |
Question 10 Explanation:
The correct answer is (C). Let $s$ be the number of minutes the singing room was rented, and let $d$ be the number of minutes the dancing room was rented.
We know that together the rooms were rented for a total of 48 minutes:
$s + d = 48$
We also know that the total cost was $\$600$.
Renting the singing room for s minutes cost $10s$.
Renting the dancing room for $d$ minutes cost $20d$.
We can combine this information to get the following equation:
$10s + 20d = 600$
We now have a system of two simultaneous equations that we can use to solve for $s$ and $d$:
$s + d = 48$
$10s + 20d = 600$
Solving this set of equations is made easier if we divide both sides of the second equation by $10$. The resulting equation is:
$1s + 2d = 60 \quad \text{or}$
$s + 2d = 60$
Our two equations are:
$s + d = 48$
$s + 2d = 60$
Subtracting the first equation from the second:
$s + 2d = 60$
$−(s + d = 48)$
$d = 12$
We know that $s + d = 48$ and $d = 12$.
Substituting we have: $s + 12 = 48$. Solving for $s$: $s = 36$
We know that together the rooms were rented for a total of 48 minutes:
$s + d = 48$
We also know that the total cost was $\$600$.
Renting the singing room for s minutes cost $10s$.
Renting the dancing room for $d$ minutes cost $20d$.
We can combine this information to get the following equation:
$10s + 20d = 600$
We now have a system of two simultaneous equations that we can use to solve for $s$ and $d$:
$s + d = 48$
$10s + 20d = 600$
Solving this set of equations is made easier if we divide both sides of the second equation by $10$. The resulting equation is:
$1s + 2d = 60 \quad \text{or}$
$s + 2d = 60$
Our two equations are:
$s + d = 48$
$s + 2d = 60$
Subtracting the first equation from the second:
$s + 2d = 60$
$−(s + d = 48)$
$d = 12$
We know that $s + d = 48$ and $d = 12$.
Substituting we have: $s + 12 = 48$. Solving for $s$: $s = 36$
Question 11 |
Two cubes with side lengths of 5 are placed adjacently as shown in the diagram below. What is the length of the interior diagonal of the newly formed rectangular prism?
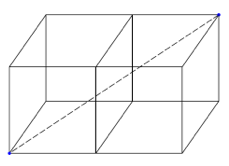
$5$ | |
$5\sqrt{5}$ | |
$5\sqrt{6}$ | |
$6\sqrt{5}$ |
Question 11 Explanation:
The correct answer is (C). The length of the diagonal is the same as a rectangular prism with dimensions of $5 × 5 × 10$, which is:
$\sqrt{5^2 + 5^2 + 10^2}$
$= \sqrt{150} = \sqrt{25 \cdot 6}$ $= 5\sqrt{6}$
$\sqrt{5^2 + 5^2 + 10^2}$
$= \sqrt{150} = \sqrt{25 \cdot 6}$ $= 5\sqrt{6}$
Question 12 |
The length of a rectangle $l$, is three times its width $w$. If the length is increased by 5 units and width is increased by 2 units, the area of a rectangle is given by which of the following expression?
$3w^2 + 11w + 10$ | |
$3w^2 − 11w + 10$ | |
$11w^2 + 3w + 10$ | |
$11w^2 − 3w − 10$ |
Question 12 Explanation:
The correct answer is (A). The relationship between length and width is given:
$l = 3w$
$\text{New area}$ $= (l + 5)( w + 2)$
$= (3w + 5)(w + 2)$
$= 3w^2 + 6w + 5w + 10$
$= 3w^2 + 11w + 10$
$l = 3w$
$\text{New area}$ $= (l + 5)( w + 2)$
$= (3w + 5)(w + 2)$
$= 3w^2 + 6w + 5w + 10$
$= 3w^2 + 11w + 10$
Question 13 |
A quadratic function has roots at $(-3, 0)$ and $(5, 0)$. Which of the following could represent the minimum point of the function?
$(1, -16)$ | |
$(1.5, -16)$ | |
$(2, -16)$ | |
$(1, 0)$ |
Question 13 Explanation:
The correct answer is (A). We are given that the two zeroes of the graph are $(-3, 0)$ and $(5, 0)$, which means that the minimum point of the function has an $x$ value of $\dfrac{-3 + 5}{2} = 1$.
The equation of this parabola is $y = (x + 3)(x - 5)$ from the given roots. This means the $y$-value of the parabola at $x = 1$ is $(1 + 3)(1 - 5) = -16$. Therefore, the correct answer is $(1, -16)$.
The equation of this parabola is $y = (x + 3)(x - 5)$ from the given roots. This means the $y$-value of the parabola at $x = 1$ is $(1 + 3)(1 - 5) = -16$. Therefore, the correct answer is $(1, -16)$.
Question 14 |
Amanda pays her cell phone company 50 dollars a month, plus 1 dollar for every minute spoken and 50 cents for each text message sent. Betty pays her cell phone company 25 dollars a month, plus 2 dollars for every minute spoken and 75 cents for each text message sent.
If both speak for 100 minutes a month, and send 200 text messages a month, how much more money will Betty spend than Amanda in 1 year?(Write down your answer.)
$\text{Click}$ $\text{here}$ $\text{to}$ $\text{see}$ $\text{the}$ $\text{correct}$ $\text{answer.}$ |
Question 14 Explanation:
The correct answer is $\$1{,}500$.
Both speak for 100 minutes and send 200 texts, in addition to the base monthly payment.
Amanda:
$50 + 1(100) + 0.5(200)$
$= 50 + 100 + 100$
$= \$250 \text{ per month}$
$250 \cdot 12 = \$3{,}000 \text{ per year}$
Betty:
$25 + 2(100) + 0.75(200)$
$= 25 + 200 + 150$
$= \$375 \text { per month}$
$375 \cdot 12 = \$4500 \text{ per year}$
The difference between their yearly costs is:
$\$4{,}500 − \$3{,}000 = \$1{,}500$
Question 15 |
A cab driver charges \$5 for the first 0.75 miles, \$8 for the subsequent 0.25 miles, and \$2 for each additional mile. How many miles can you travel in the cab if you paid \$50?
(Write down your answer.)
$\text{Click}$ $\text{here}$ $\text{to}$ $\text{see}$ $\text{the}$ $\text{correct}$ $\text{answer.}$ |
Question 15 Explanation:
The correct answer is $19.5$.
Let $m$ be the miles traveled for $\$50$. Then $m$ miles can be broken down, based on each fare segment. This must to add up to $m$ miles.
$m = 0.75 + 0.25 + (m − 1)$
The first mile is included in the $m$. Now apply the fares to each segment:
$5 + 8 + (m − 1) \cdot 2 = 50$
$13 + 2m − 2 = 50$
$2m = 39$
$m = 19.5 \text{ miles}$
Question 16 |
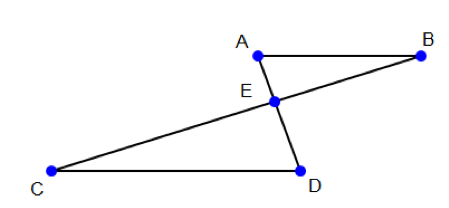
In the diagram shown above, $AE$ has a length of $3$. $AD$ has a length of $9$. $AB$ and $CD$ are parallel. What is the ratio of the area of triangle $CED$ to triangle $AEB$?
(Write down your answer.)
$\text{Click}$ $\text{here}$ $\text{to}$ $\text{see}$ $\text{the}$ $\text{correct}$ $\text{answer.}$ |
Question 16 Explanation:
The correct answer is $4$.
$∠ CED ≅ ∠ BEA$ (vertical angles)
Since $AB$ and $CD$ are parallel, $∠EBA ≅ ∠ECD$ and $∠EAB ≅ ∠EDC$ (alternate interior angles).
This means that triangles $ABE$ and $ECD$ are similar by AAA similarity. $AE = 3$ and $ED = 6$. This means that the side lengths of the larger triangle are twice the smaller triangle. Hence, the area of the larger triangle is $2^2 = 4$ times the area of the smaller triangle.
Question 17 |
What is the absolute value of the sum of the solutions to the polynomial shown below?
$x^2 − 15 = 2x$(Write down your answer.)
$\text{Click}$ $\text{here}$ $\text{to}$ $\text{see}$ $\text{the}$ $\text{correct}$ $\text{answer.}$ |
Question 17 Explanation:
The correct answer is $2$.
$x^2 − 15 = 2x$
When solving a quadratic, you should begin by getting the $x^2$, $x$, and constant terms on one side of the equation. To do so, we subtract 2$x$ from both sides to get:
$x^2 − 2x − 15 = 0$
The polynomial $x^2 − 2x − 15$ can be factored, giving:
$(x − 5)(x + 3) = 0$
The solutions (or “zeros”) to this are $x = −3$ and $x = 5$.
$|−3 + 5| = |2| = 2$
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 17 questions to complete.
|
List |
More PSAT Practice:
PSAT Math: Calculator >>
PSAT Main Menu >>
